小白学机器学习西瓜书-第三章对数几率回归
小白学机器学习西瓜书-第三章对数几率回归
- 3.3 对数几率回归
-
- 3.3.1 对数几率函数
- 3.3.1 估计参数
上一部分我们介绍了线性回归,包括简单的二元回归和多元回归,这两个主要解决的是拟合预测的问题,但如果我们碰到的并不是预测连续性值的问题而是分类问题呢,对数几率回归可能解决这种分类问题。接下来我们来总结对数几率回归部分的原理和公式推导
上一部分的link:小白学机器学习西瓜书-第三章线性回归
3.3 对数几率回归
3.3.1 对数几率函数
针对分类问题,我们没办法用线性回归模型来进行解决,主要原因是因为线性回归模型主要针对的是连续型Y值,分类问题则面对的是离散型Y值。
但这也并不是线性回归完全无关,我们只需要稍微改进一下线性回归的模型,加一个映射函数,使得能够将线性回归得出的值化为分类问题的值即可。
首先我们考虑一个简单的分类任务,其y值仅包含两个值0和1,即 y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1},由于线性回归产生的 z = w T x + b z=w^Tx+b z=wTx+b 是连续值,所以我们需要将连续值转换为0和1,最理想的函数就是单位阶跃函数。他的意思是,如果线性回归的z值为正,则分类为1,如果线性回归的z值为负,则分类为0。
y = { 0 z < 0 0.5 z = 0 1 z > 0 (1) y=\begin{cases} 0 & z < 0 \\ 0.5 & z=0 \\ 1 & z>0 \tag{1} \end{cases} y=⎩⎪⎨⎪⎧00.51z<0z=0z>0(1)
但单位阶跃函数的缺点在于它并不连续,所以很不方便,因此我们需要找到一个单调可微的性质和单位阶跃函数类似的函数。对数几率函数就是一个常见的替代函数。
y = 1 1 + e − z (2) y=\frac{1}{1+e^{-z}} \tag{2} y=1+e−z1(2)
他的图像差不多是这样子的
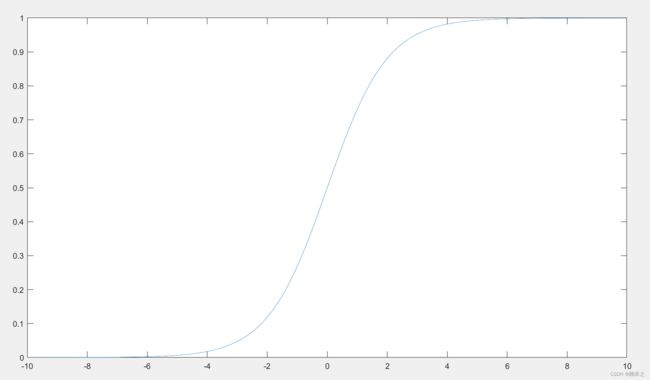
可以看到,对数几率函数的形状呈S型,是Sigmoid函数的一种
我们将线性回归中的因变量带入对数几率函数中的自变量,即
y = 1 1 + e − ( w T x + b ) (3) y=\frac{1}{1+e^{-(w^Tx+b)}} \tag{3} y=1+e−(wTx+b)1(3)
我们将式(3)变换一下
1 y = 1 + e − ( w T x + b ) e − ( w T x + b ) = 1 − y y w T x + b = − l n ( 1 − y y ) w T x + b = l n ( y 1 − y ) (4) \begin{aligned} \frac{1}{y}&=1+e^{-(w^Tx+b)}\\ e^{-(w^Tx+b)}&=\frac{1-y}{y}\\ w^Tx+b&=-ln(\frac{1-y}{y})\\ w^Tx+b&=ln(\frac{y}{1-y}) \tag{4} \end{aligned} y1e−(wTx+b)wTx+bwTx+b=1+e−(wTx+b)=y1−y=−ln(y1−y)=ln(1−yy)(4)
如果将式(4)的y视作样本值为正例的可能性,那么1-y就是其为反例的可能性,两者的比值即为 y 1 − y \frac{y}{1-y} 1−yy,称为几率,反映了样本为正例的相对可能性,对其取对数就称为对数几率,即为式(4)的右边部分
而式(4)的左边部分为线性回归的值,因此,其实这一过程是用线性回归模型的预测结果逼近真实标记的对数几率
3.3.1 估计参数
接下来我们对式(3)中的w和b进行参数估计,前面我们将y视作为正例的可能性,那么式(4)可以改写为
w T x + b = l n ( y 1 − y ) l n ( p ( y = 1 ∣ x ) 1 − p ( y = 1 ∣ x ) ) = w T x + b p ( y = 1 ∣ x ) = ( 1 − p ( y = 1 ∣ x ) ) e w T x + b p ( y = 1 ∣ x ) = e w T x + b − p ( y = 1 ∣ x ) e w T x + b p ( y = 1 ∣ x ) = e w T x + b 1 + e w T x + b (5) \begin{aligned} w^Tx+b&=ln(\frac{y}{1-y})\\ ln(\frac{p(y=1 \mid x)}{1-p(y=1 \mid x)})&=w^Tx+b\\ p(y=1 \mid x)&=(1-p(y=1 \mid x))e^{w^Tx+b}\\ p(y=1 \mid x)&=e^{w^Tx+b}-p(y=1 \mid x)e^{w^Tx+b}\\ p(y=1 \mid x)&=\frac{e^{w^Tx+b}}{1+e^{w^Tx+b}} \tag{5} \end{aligned} wTx+bln(1−p(y=1∣x)p(y=1∣x))p(y=1∣x)p(y=1∣x)p(y=1∣x)=ln(1−yy)=wTx+b=(1−p(y=1∣x))ewTx+b=ewTx+b−p(y=1∣x)ewTx+b=1+ewTx+bewTx+b(5)
由于y仅有两种情况0和1,从而 p ( y = 1 ∣ x ) = 1 − p ( y = 0 ∣ x ) p(y=1 \mid x)=1-p(y=0 \mid x) p(y=1∣x)=1−p(y=0∣x)
因此
1 − p ( y = 0 ∣ x ) = e w T x + b 1 + e w T x + b p ( y = 0 ∣ x ) = 1 1 + e w T x + b (6) \begin{aligned} 1-p(y=0 \mid x)&=\frac{e^{w^Tx+b}}{1+e^{w^Tx+b}}\\ p(y=0 \mid x)&=\frac{1}{1+e^{w^Tx+b}} \tag{6} \end{aligned} 1−p(y=0∣x)p(y=0∣x)=1+ewTx+bewTx+b=1+ewTx+b1(6)
这里的估计参数的方法涉及极大似然法,其思想为,已知某个参数能使得这个样本出现的概率最大,那么我们就将这个参数作为估计的真实值,即可表示为式(7),只要找到使得式(7)最大的w和b值即可
l ( w , b ) = ∑ i = 1 m l n p ( y i ∣ x i ; w , b ) (7) l(w,b)=\sum^m_{i=1}lnp(y_i \mid x_i;w,b) \tag{7} l(w,b)=i=1∑mlnp(yi∣xi;w,b)(7)
令 β = ( w ; b ) , x ^ = ( x ; 1 ) \beta =(w;b),\hat{x}=(x;1) β=(w;b),x^=(x;1),那么 w T + b w^T+b wT+b可以简写为 β T x ^ \beta ^T\hat{x} βTx^(这一部分上一部分有介绍)小白学机器学习西瓜书-第三章线性回归
p ( y = 1 ∣ x ) = e w T x + b 1 + e w T x + b = > e β T x ^ 1 + e β T x ^ p(y=1 \mid x)=\frac{e^{w^Tx+b}}{1+e^{w^Tx+b}}=>\frac{e^{\beta ^T\hat{x}}}{1+e^{\beta ^T\hat{x}}} p(y=1∣x)=1+ewTx+bewTx+b=>1+eβTx^eβTx^
p ( y = 0 ∣ x ) = 1 1 + e w T x + b = > 1 1 + e β T x ^ p(y=0 \mid x)=\frac{1}{1+e^{w^Tx+b}}=>\frac{1}{1+e^{\beta ^T\hat{x}}} p(y=0∣x)=1+ewTx+b1=>1+eβTx^1
设 p 1 ( x ^ ; β ) = p ( y = 1 ∣ x ^ ; β ) , p 0 ( x ^ ; β ) = p ( y = 0 ∣ x ^ ; β ) = 1 − p 1 ( x ^ ; β ) p_1(\hat{x}; \beta )=p(y=1 \mid \hat{x};\beta),p_0(\hat{x}; \beta )=p(y=0 \mid \hat{x};\beta)=1-p_1(\hat{x}; \beta ) p1(x^;β)=p(y=1∣x^;β),p0(x^;β)=p(y=0∣x^;β)=1−p1(x^;β)
似然项即可写为
p ( y i ∣ x i ; w , b ) = y i p 1 ( x i ^ ; β ) + ( 1 − y i ) p 0 ( x i ^ ; β ) (8) p(y_i \mid x_i; w,b )=y_ip_1(\hat{x_i}; \beta )+(1-y_i)p_0(\hat{x_i}; \beta ) \tag{8} p(yi∣xi;w,b)=yip1(xi^;β)+(1−yi)p0(xi^;β)(8)
可以看到,当 y i y_i yi为1时,式子为 p 1 ( x i ^ ; β ) p_1(\hat{x_i}; \beta ) p1(xi^;β),当 y i y_i yi为0时,式子为 p 0 ( x i ^ ; β ) p_0(\hat{x_i}; \beta ) p0(xi^;β),只要使得这个式子组合的所有样本的函数最大,即可找到最优的w和b值
而之前我们已经计算出了
p ( y = 1 ∣ x ) = e β T x ^ 1 + e β T x ^ p(y=1 \mid x)=\frac{e^{\beta ^T\hat{x}}}{1+e^{\beta ^T\hat{x}}} p(y=1∣x)=1+eβTx^eβTx^
p ( y = 0 ∣ x ) = 1 1 + e β T x ^ p(y=0 \mid x)=\frac{1}{1+e^{\beta ^T\hat{x}}} p(y=0∣x)=1+eβTx^1
将他们和式(8)一起带入似然函数,为了方便,我们将 β T x ^ \beta ^T\hat{x} βTx^简写为 z z z ,则
l ( β ) = ∑ i = 1 m l n ( y i e z 1 + e z + ( 1 − y i ) 1 1 + e z ) l ( β ) = ∑ i = 1 m l n ( y i ( e z − 1 ) + 1 1 + e z ) l ( β ) = ∑ i = 1 m l n ( ( y i ( e z − 1 ) + 1 ) − l n ( 1 + e z ) ) (9) \begin{aligned} l(\beta)&= \sum^m_{i=1}ln(y_i\frac{e^z}{1+e^z}+(1-y_i)\frac{1}{1+e^z})\\ l(\beta)&= \sum^m_{i=1}ln(\frac{y_i(e^z-1)+1}{1+e^z})\\ l(\beta)&= \sum^m_{i=1}ln((y_i(e^z-1)+1)-ln(1+e^z))\\ \tag{9} \end{aligned} l(β)l(β)l(β)=i=1∑mln(yi1+ezez+(1−yi)1+ez1)=i=1∑mln(1+ezyi(ez−1)+1)=i=1∑mln((yi(ez−1)+1)−ln(1+ez))(9)
从式(9)可知,如果 y i y_i yi为1时,式子为
l ( β ) = ∑ i = 1 m l n ( ( e z − 1 + 1 ) − l n ( 1 + e z ) ) l ( β ) = ∑ i = 1 m ( z − l n ( 1 + e z ) ) (10) \begin{aligned} l(\beta)&= \sum^m_{i=1}ln((e^z-1+1)-ln(1+e^z))\\ l(\beta)&= \sum^m_{i=1}(z-ln(1+e^z)) \tag{10} \end{aligned} l(β)l(β)=i=1∑mln((ez−1+1)−ln(1+ez))=i=1∑m(z−ln(1+ez))(10)
如果 y i y_i yi为0时,式子为
l ( β ) = ∑ i = 1 m ( l n ( 1 ) − l n ( 1 + e z ) ) l ( β ) = ∑ i = 1 m − l n ( 1 + e z ) (11) \begin{aligned} l(\beta)&= \sum^m_{i=1}(ln(1)-ln(1+e^z))\\ l(\beta)&=\sum^m_{i=1}-ln(1+e^z) \tag{11} \end{aligned} l(β)l(β)=i=1∑m(ln(1)−ln(1+ez))=i=1∑m−ln(1+ez)(11)
因此,我们可以将式(10)和(11)写一个通式
l ( β ) = ∑ i = 1 m ( y i z − l n ( 1 + e z ) ) (12) l(\beta)=\sum^m_{i=1}(y_iz-ln(1+e^z))\tag{12} l(β)=i=1∑m(yiz−ln(1+ez))(12)
在将 z = β T x ^ z=\beta ^T\hat{x} z=βTx^回代,则变为
l ( β ) = ∑ i = 1 m ( y i β T x ^ − l n ( 1 + e β T x ^ ) ) (12) l(\beta)=\sum^m_{i=1}(y_i\beta ^T\hat{x}-ln(1+e^{\beta ^T\hat{x}}))\tag{12} l(β)=i=1∑m(yiβTx^−ln(1+eβTx^))(12)
找到使得式(12)最大的 β \beta β值
由于最大化函数不如最小化好求,因此,将式(12)转化为求最小值
l ( β ) = ∑ i = 1 m ( − y i β T x ^ + l n ( 1 + e β T x ^ ) ) (13) l(\beta)=\sum^m_{i=1}(-y_i\beta ^T\hat{x}+ln(1+e^{\beta ^T\hat{x}}))\tag{13} l(β)=i=1∑m(−yiβTx^+ln(1+eβTx^))(13)
这个式子由牛顿法迭代求解带公式即可