LCS,LIS,LCIS
LCS: 以下讲解来自:http://blog.csdn.net/yysdsyl/article/details/4226630
【问题】 求两字符序列的最长公共字符子序列
问题描述:字符序列的子序列是指从给定字符序列中随意地(不一定连续)去掉若干个字符(可能一个也不去掉)后所形成的字符序列。令给定的字符序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk-1”是X的子序列,存在X的一个严格递增下标序列<i0,i1,…,ik-1>,使得对所有的j=0,1,…,k-1,有xij=yj。例如,X=“ABCBDAB”,Y=“BCDB”是X的一个子序列。
考虑最长公共子序列问题如何分解成子问题,设A=“a0,a1,…,am-1”,B=“b0,b1,…,bm-1”,并Z=“z0,z1,…,zk-1”为它们的最长公共子序列。不难证明有以下性质:
(1) 如果am-1=bn-1,则zk-1=am-1=bn-1,且“z0,z1,…,zk-2”是“a0,a1,…,am-2”和“b0,b1,…,bn-2”的一个最长公共子序列;
(2) 如果am-1!=bn-1,则若zk-1!=am-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列;
(3) 如果am-1!=bn-1,则若zk-1!=bn-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列。
这样,在找A和B的公共子序列时,如有am-1=bn-1,则进一步解决一个子问题,找“a0,a1,…,am-2”和“b0,b1,…,bm-2”的一个最长公共子序列;如果am-1!=bn-1,则要解决两个子问题,找出“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列和找出“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列,再取两者中较长者作为A和B的最长公共子序列。
求解:
引进一个二维数组c[][],用c[i][j]记录X[i]与Y[j] 的LCS 的长度,b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向。
我们是自底向上进行递推计算,那么在计算c[i,j]之前,c[i-1][j-1],c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j],就可以计算出c[i][j]。
问题的递归式写成:
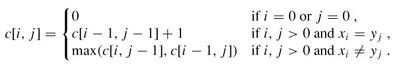
回溯输出最长公共子序列过程:
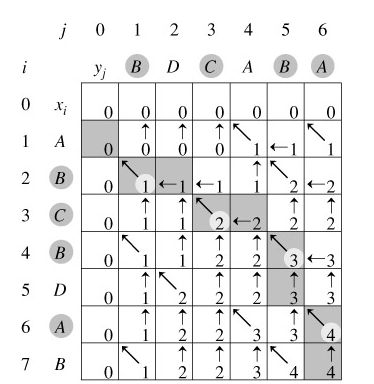
接下来放一个输出最长公共子序列的长度及序列的代码:
1 #include <iostream> 2 #include <string> 3 #include <string.h> 4 using namespace std; 5 int c[100][100]; 6 int b[100][100]; 7 int LCS_Length(string x,string y) 8 { 9 int m=x.length(); 10 int n=y.length(); 11 int i,j; 12 memset(c,0,sizeof(c));//根据递归方程的第一种情况,先初始化数组c[][] 13 for(i=1;i<=m;i++) 14 for(j=1;j<=n;j++) 15 {//递归方程case 2 16 if(x[i-1] == y[j-1]) 17 { 18 c[i][j]=c[i-1][j-1]+1; 19 b[i][j]=1; //表示 20 } 21 else if(c[i-1][j] >= c[i][j-1]) //下面是递归方程case3 22 { 23 c[i][j]=c[i-1][j]; 24 b[i][j]=2; //表示↑ 25 } 26 else 27 { 28 c[i][j]=c[i][j-1];; 29 b[i][j]=3; //表示← 30 } 31 } 32 return c[m][n]; 33 } 34 void Print_LCS(string X,int i,int j)//输出最优解 35 { 36 if( (i == 0) || (j == 0) ) 37 return; 38 if(b[i][j] == 1) 39 { 40 Print_LCS(X,i-1,j-1); 41 cout<<X[i-1]<<" "; 42 } 43 else if(b[i][j] == 2) 44 Print_LCS(X,i-1,j); 45 else 46 Print_LCS(X,i,j-1); 47 } 48 49 int main() 50 { 51 string X,Y; 52 while(cin>>X>>Y) 53 { 54 int p=LCS_Length(X,Y); 55 cout<<"这两个字符串的LCS为:"<<p<<endl; 56 cout<<"该公共子序列为:"; 57 Print_LCS(X,X.length(),Y.length()); 58 cout<<endl; 59 } 60 return 0; 61 }
接下来是这一次比赛的题目:
A 大意是:求最长公共子序列。 Common Subsequence HDU 1159 62MS
1 #include<stdio.h> 2 #include<iostream> 3 #include<string.h> 4 #include<string> 5 using namespace std; 6 char a[1010],b[1010]; 7 short dp[1010][1010]; 8 int n,l1,l2; 9 int maxx(int i,int j) 10 { 11 return i>j?i:j; 12 } 13 int main() 14 { 15 while(~scanf("%s %s",a,b)) 16 { 17 l1=strlen(a); //长度 18 l2=strlen(b); 19 int i,j; 20 memset(dp,0,sizeof(dp)); 21 for(i=1;i<=l1;i++) 22 for(j=1;j<=l2;j++) 23 { 24 if(a[i-1]==b[j-1]) 25 dp[i][j]=dp[i-1][j-1]+1; 26 else 27 dp[i][j]=maxx(dp[i-1][j],dp[i][j-1]); 28 } 29 printf("%d\n",dp[l1][l2]); 30 } 31 }
B 大意是:求回文字符串要不的个数。方法:把字符串a,反序得b,在把a,b的最长公共子序列求出来,用a的长度n-最长公共子序列的长度。
Palindrome HDU 1513 484MS
先是代码,再是我的吐槽。
1 #include<stdio.h> 2 #include<string.h> 3 char a[5001],b[5001]; 4 short dp[2][5001]; 5 int maxx(int i,int j) 6 { 7 return i>j?i:j; 8 } 9 int main() 10 { 11 int n,j,i; 12 while(~scanf("%d",&n)) 13 { 14 scanf("%s",a); 15 memset(dp,0,sizeof(dp)); 16 for(i=0;i<n;i++) //反序得到b 17 b[i]=a[n-i-1]; 18 for(i=1;i<=n;i++) 19 for(j=1;j<=n;j++) 20 { 21 if(a[i-1]==b[j-1]) 22 dp[i%2][j]=dp[(i-1)%2][j-1]+1; 23 else 24 dp[i%2][j]=maxx(dp[(i-1)%2][j],dp[i%2][j-1]); 25 } 26 printf("%d\n",n-dp[n%2][n]); 27 } 28 return 0; 29 }
本来我的dp是开的dp[5001][5001],本来在POJ是没有超内存的,因为在POJ的内存限制的60000+,但是HDU和我们的比赛是32000+.......少了一半多,开dp[5001][5001]的内存是49000+,所以超内存了。但是因为在扫描的时候,每次只扫描两行,所以dp[i][j]就可以变为dp[i%2][j],所以dp[5001][5001]就可以改为dp[2][5002],这样内存就大大减小了。 本来我认为i,j可以分别%2,因为实际扫的时候只有关4个点:1自己所在的点,2右边的点,3下面的点,4斜下方的点。但是现在还没有找到可行的方法。
先是非最长公共子序列的代码: 0ms
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <vector> 5 using namespace std; 6 #define N 1010 7 char a[N],b[N]; 8 vector<char>c[30]; 9 int main() 10 { 11 int i,j,k,m,T,t=1; 12 scanf("%d",&T); 13 char x,y; 14 while(T--) 15 { 16 scanf("%s%s",a,b); 17 scanf("%d",&m); 18 memset(c,0,sizeof(c)); 19 while(m--) 20 { 21 cin>>x>>y; 22 c[(int)(x-'a')].push_back(y); //可以变的记录下来 23 } 24 for(i=0,k=0;a[k]&&b[i];i++) 25 { 26 if(b[i]==a[k]) //如果相等,两列都向前+1 27 { 28 k++; 29 continue; 30 } 31 for(j=c[b[i]-'a'].size()-1;j>=0;j--) 32 if(c[b[i]-'a'][j]==a[k]) //不同的时候如果可以变得和a,一样则+1 33 { 34 k++; 35 break; 36 } 37 } 38 printf("Case #%d: ",t++); 39 if(k>=strlen(a)) 40 printf("happy\n"); 41 else printf("unhappy\n"); 42 } 43 return 0; 44 }
再是求最长公共子序列的代码: 218MS
1 #include<iostream> 2 #include<string.h> 3 #include<string> 4 using namespace std; 5 int dp[1005][1005]; 6 bool has[128][128]; //这个要开大一点 7 int maxi(int x,int y) 8 { 9 if(x>y) 10 return x; 11 else return y; 12 } 13 int main() 14 { 15 int i,j,t,m,count=0,len1,len2; 16 char a,b; 17 string str1,str2; 18 cin>>t; 19 while(t--) 20 { 21 count=count+1; 22 cin>>str1>>str2; 23 len1=str1.size(); 24 len2=str2.size(); 25 memset(dp,0,sizeof(dp)); 26 memset(has,0,sizeof(has)); 27 cin>>m; 28 for(j=1;j<=m;j++) 29 { 30 cin>>a>>b; 31 has[a][b]=1; 32 } 33 for(i=1;i<=len1;i++) 34 for(j=1;j<=len2;j++) 35 { 36 if(str1[i-1]==str2[j-1]||has[str2[j-1]][str1[i-1]]==1) //或者可以变一样的~~~~~ 37 dp[i][j]=dp[i-1][j-1]+1; 38 else dp[i][j]=maxi(dp[i-1][j],dp[i][j-1]); 39 } 40 cout<<"Case #"<<count<<": "; 41 if(dp[len1][len2]==len1) 42 cout<<"happy"<<endl; 43 else cout<<"unhappy"<<endl; 44 } 45 return 0; 46 }
D 大意是:求最少有几个下降序列 最少拦截系统 HDU 1257 有个说法是求最长上升子序列的长度。
先是DP: 15MS 来自:http://blog.csdn.net/a_eagle/article/details/7237067
1 #include <stdio.h>//dp[i]表示第i个导弹飞过来时需要的最少拦截装置 2 #include <string.h> 3 int main() 4 { 5 int n,i,j,max,h[10001],dp[10001]; 6 while(~scanf("%d",&n)) 7 { 8 memset(dp,0,sizeof(dp));//初始化拦截装置都为0 9 max=-1; 10 for(i=1;i<=n;i++) 11 scanf("%d",&h[i]);//飞来的高度 12 for(i=1;i<=n;i++) 13 for(j=i-1;j>=0;j--) 14 if(h[i]>h[j]&&dp[i]<dp[j]+1)//如果在拦截中出现了非单调递减的 15 dp[i]=dp[j]+1; 16 for(i=1;i<=n;i++) 17 if(dp[i]>max) 18 max=dp[i]; //取最大值 19 printf("%d\n",max); 20 } 21 return 0; 22 }
再是贪心: 46MS
1 #include <iostream> 2 #include <string> 3 #include <algorithm> 4 #define MAX 100000000 5 using namespace std; 6 int height[10000]; 7 int top; 8 void arrange(int n) 9 { 10 int i; 11 sort(height,height+top+1); 12 for(i=0;i<=top;i++) 13 if(height[i]>=n) 14 { 15 height[i]=n; 16 break; 17 } 18 if(i==top+1)//引入新的导弹系统 19 { 20 top++; 21 height[top]=n; 22 } 23 } 24 int main() 25 { 26 int t; 27 while(cin>>t) 28 { 29 top=0; 30 height[0]=MAX;//初始可以阻挡任何高度 31 int height; 32 for(int i=0;i<t;i++) 33 { 34 cin>>height; 35 arrange(height); 36 } 37 cout<<top+1<<endl; 38 } 39 }
同E一样的方法......三观尽毁..... 15MS
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 class Do 7 { 8 public: 9 int x,id; 10 }D[20000]; 11 int main() 12 { 13 int n; 14 while(~scanf("%d",&n)) 15 { 16 int i,minn; 17 memset(D,0,sizeof(D)); 18 for(i=0;i<n;i++) 19 scanf("%d",&D[i].x); 20 int number=0,j; 21 for(i=0;i<n;i++) 22 if(D[i].id==0) //找到最大的没有标记的 23 { 24 minn=D[i].x; 25 number++; 26 for(j=i+1;j<n;j++) 27 if(D[j].x<minn && D[j].id==0) //小于最小高度&&没有被标记 28 { 29 D[j].id=1; 30 minn=D[j].x; //更新最小高度 31 } 32 } 33 printf("%d\n",number); 34 } 35 return 0; 36 }
E 大意是:有N个娃娃,有自己高度和大小,小的可以放到大娃娃里,求最后剩下几个娃娃。 Nested Dolls HDU 1677
代码: 78MS
1 #include <iostream> 2 #include <algorithm> 3 #include <stdio.h> 4 using namespace std; 5 struct node 6 { 7 int w,h; 8 }; 9 node a[20001]; 10 bool cmp(node a,node b) 11 { 12 if(a.w!=b.w) //按W排序,接下来的就不用管W了,只要比h的大小 13 return a.w>b.w; 14 return a.h<b.h; 15 } 16 int visit[20001]; 17 int main() 18 { 19 int t; 20 scanf("%d",&t); 21 while(t--) 22 { 23 int m; 24 cin>>m; 25 for(int i=0;i<m;i++) 26 scanf("%d %d",&a[i].w,&a[i].h); 27 sort(a,a+m,cmp); //排序 28 int cnt=0; 29 visit[cnt++]=a[0].h; 30 for(int i=1;i<m;i++) 31 { 32 if(a[i].h>=visit[cnt-1]) //高度大于等于前面w最小的娃娃的h,则又开一个新的娃娃 33 visit[cnt++]=a[i].h; 34 else 35 { 36 int l=0,r=cnt; 37 while(l<r) //二分找到可以放进去的最小的娃娃 38 { 39 int mid=(l+r)/2; 40 if(visit[mid]>a[i].h)r=mid; 41 else l=mid+1; 42 } 43 visit[l]=a[i].h; 44 } 45 } 46 cout<<cnt<<endl; 47 } 48 return 0; 49 }
下面介绍另一种方法: 468MS
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 class Dolls 7 { 8 public: 9 int x,y,id; 10 }D[20020]; 11 bool comp(Dolls a,Dolls b) 12 { 13 if(a.x==b.x) return a.y<b.y; //同上 14 return a.x>b.x; 15 } 16 int main() 17 { 18 int t,n; 19 scanf("%d",&t); 20 while(t--) 21 { 22 int i,minn; 23 scanf("%d",&n); 24 memset(D,0,sizeof(D)); 25 for(i=0;i<n;i++) 26 scanf("%d%d",&D[i].x,&D[i].y); 27 sort(D,D+n,comp); //排序 28 int number=0,j; 29 for(i=0;i<n;i++) 30 if(D[i].id==0) //找到W最大的没有标记的娃娃 31 { 32 minn=D[i].y; 33 number++; 34 for(j=i+1;j<n;j++) 35 if(D[j].y<minn && D[j].id==0) //高度《这个娃娃,并且没有被标记 36 { 37 D[j].id=1; //标记 38 minn=D[j].y; //更新高度 39 } 40 } 41 printf("%d\n",number); 42 } 43 return 0; 44 }
插花一下,先讲下最长上升子序列。
1 #include <stdio.h> 2 #define MAX 100000 3 #define INF 100000000 4 int a[MAX],c[MAX],len; 5 int find(int L,int R,int x) 6 { 7 if(L==R) return L; 8 int mid=(L+R)>>1; 9 if(c[mid]<x) return find(mid+1,len,x); //二分 10 else return find(L,mid,x); //二分 11 } 12 int main() 13 { 14 int i,n,j; 15 while(scanf("%d",&n)!=EOF) 16 { 17 for(i=0;i<n;i++) 18 scanf("%d",&a[i]); 19 len=0; c[0]=-INF; 20 for(i=0;i<n;i++) 21 { 22 if(a[i]>c[len]) j=++len; 23 else j=find(1,len,a[i]); 24 c[j]=a[i]; 25 } 26 printf("%d\n",len); 27 } 28 }
另一种方法:
1 #include <stdio.h> 2 #include <string.h> 3 int main() 4 { 5 int n,a[1000],map[1000],i,j,maxx,number; 6 while(~scanf("%d",&n)) 7 { 8 memset(map,0,sizeof(map)); 9 memset(c,0,sizeof(c)); 10 number =0; 11 for(i=0;i<n;i++) 12 scanf("%d",&a[i]); 13 for(i=0;i<n;i++) 14 if(map[i]==0) //找到第一个没被标记的 15 { 16 map[i]=1; 17 number++; //总数+1 19 maxx=a[i]; 20 for(j=i+1;j<n;j++) 21 if(map[j]==0&&a[j]<=maxx) //大于前面的数并且未被标记 22 {
map[j]=0; 25 maxx=a[j]; //更新最大数 26 } 27 } printf("%d\n",number); 33 } 34 return 0; 35 }
E 大意是求最长公共上升子序列。 15ms
1 #include<cstdio> 2 #include<cstring> 3 int f[1005],a[1005],b[1005],i,j,t,n1,n2,max; 4 int main() 5 { 6 scanf("%d",&t); 7 while(t--) 8 { 9 scanf("%d",&n1); 10 for(i=1;i<=n1;i++) 11 scanf("%d",&a[i]);
scanf("%d",&n2); 12 for(i=1;i<=n2;i++) 13 scanf("%d",&b[i]); 14 memset(f,0,sizeof(f)); 15 for(i=1;i<=n1;i++) 16 { 17 max=0; 18 for(j=1;j<=n2;j++) 19 { 20 if (a[i]>b[j]&&max<f[j]) 21 max=f[j]; 22 if (a[i]==b[j]) 23 f[j]=max+1; 24 } 25 } 26 max=0; 27 for(i=1;i<=n2;i++) 28 if (max<f[i]) 29 max=f[i]; 30 printf("%d\n",max); 31 } 32 }
F 大意是:求最长回文上升子序列的长度。 0MS
1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 int n,ans,a[201],dp[201]; 5 inline void Max(int &a,const int b){if(b>a) a=b;} 6 int main() 7 { 8 int T; 9 scanf("%d",&T); 10 while(T--) 11 { 12 scanf("%d",&n); 13 memset(dp,0,sizeof dp); 14 for(int i=0;i<n;i++) 15 scanf("%d",&a[i]); 16 ans=1; 17 for(int k=n-1;k>=0;k--) 18 { 19 int mx=0; 20 for(int i=0;i<=k;i++) 21 { 22 if(a[i]<a[k]) 23 Max(mx,dp[i]); 24 else if(a[i]==a[k]) 25 dp[i]=mx+1; 26 if(i<k) 27 Max(ans,dp[i]*2); 28 else 29 Max(ans,dp[i]*2-1); 30 } 31 } 32 printf("%d\n",ans); 33 } 34 return 0; 35 }