「C++小游戏教程」基本技巧(1)——随机化

0. 引言

小游戏中时常要用到随机数，今天就来谈谈这个所谓的“随机”。

---

1. 随机数 rand()

我们要使用随机数（严格意义上是伪随机）的话，C++ 中就有 rand() 来提供了这一操作。
rand() 返回值是整数。在不同系统的编译器下，返回值的范围不同，我们姑且认为足够我们使用。
设我们要获取数 $x$，逐步推导：

• 当 $x\in [0,100]$ 时，可以写成 rand()%101；
• 当 $x\in [1,100]$ 时，可以转化为 $x^{\prime }+1(x^{\prime }\in [0,99])$，写成 rand()%100+1；
• 当 $x\in [l,r]$ 时，可以转化为 $x^{\prime }+l(x^{\prime }\in [0,r-l])$，写成 rand()%(r-l+1)+l。

可现实总是不尽如人意：

为什么每次随机出来的序列都是一样的呢？这里我们就要讲到下面的东西了——

---

2. 设置随机种子 srand()

毕竟是伪随机，所以每次生成的随机序列需要有一个初始的随机种子（无符号整数），srand() 提供了这一操作。
比如设置随机种子为 $114514$，可以写成 srand(114514);。
然而——

这意味着种子要随机。

---

3. 时间 time()

time() 返回从 $\mathrm{1970.1.1}$ 至今的秒数，参数直接填 NULL 或 $0$（也就是空指针）即可。
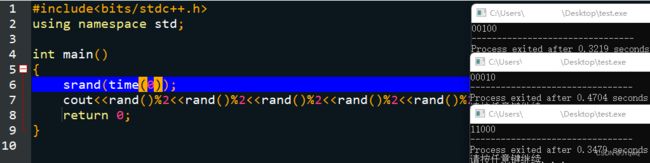
设置为种子，也就是 srand(time(0));。
效果显著：

---

4. 随机排列 random_shuffle()

如果有一个数组 $a$，如何让其进行随机排列呢？
C++ 有函数 random_shuffle()。
参数和用法与 sort() 类似，直接调用即可。
示例代码：

#include
using namespace std;

int main()
{
	srand(time(0)); 
	int n,a[105];
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	random_shuffle(a+1,a+n+1);
	for(int i=1;i<=n;i++)
	{
		cout<<a[i]<<' '; 
	}
 	return 0;
}

效果：

---

5. 随机基本案例

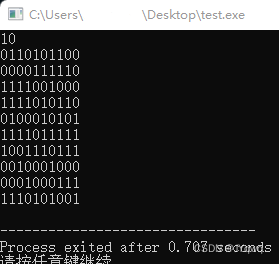
5-1. 随机 01 矩阵

给定边长 $n$，要求生成一个随机 01 矩阵。

示例代码：

#include
using namespace std;

int main()
{
	srand(time(0)); 
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cout<<rand()%2;
		}
		cout<<endl;
	}
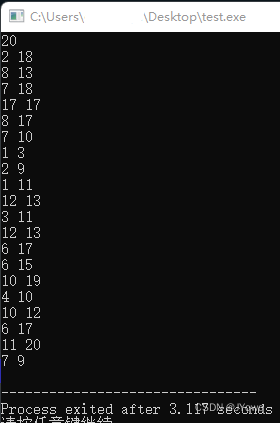
 	return 0;
}

效果：

5-2. 随机区间

给定 $n$，要求生成 $n$ 个区间 $[l,r](l\le r)$，并且这些区间是 $[1,n]$ 的子区间。

每次分别对于 $l,r$ 随机，然后调整 $l,r$ 大小位置。
示例代码：

#include
using namespace std;

int main()
{
	srand(time(0)); 
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int l=rand()%n+1,r=rand()%n+1;
		if(l>r) swap(l,r);//防止 l>r
		cout<<l<<' '<<r<<endl;
	}
 	return 0;
}

效果：

5-3. 随机浮点数

给定 $n$ 和 $k$，要求生成 $n$ 个 $[0,n]$ 的 $k$ 位浮点数（不可以有后缀 $0$）。

分成整数部分和小数部分考虑。
整数部分生成 $[0,n]$ 的整数，小数部分生成 $k$ 位 $[0,9]$ 的数（在位数允许时，可以生成一个 $[0,10^k-1]$ 的整数代替小数）。
当然，要特判整数为 $n$ 的情况。若小数部分 $>0$，就不在 $[0,n]$ 内了。
处理后缀 $0$ 时，只要把其存进字符串处理即可。
示例代码：

#include
using namespace std;

int main()
{
	srand(time(0)); 
	int n,k;
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		int d=rand()%(n+1);
		cout<<d;
		if(d==n)
		{
			cout<<endl;
			continue;
		}
		string s=".";
		for(int j=1;j<=k;j++)
		{
			s+=(char)(rand()%10+48);
		}
		while(s[s.size()-1]=='0'&&s.size()>2) s.erase(s.size()-1);//防止后缀 0
		cout<<s<<endl;
	}
 	return 0;
}

效果：

5-4. 随机整数

给定 $n,l,r(l,r\in \mathbb{Z},l\le r)$，要求生成 $n$ 个整数 $x(x\in [l,r])$。
可能含有负数，该怎么办呢？
分三类讨论：

• 当 $l\le r\le 0$ 时，先输出 -，然后生成 $[|r|,|l|]$ 范围的整数。
• 当 $l\le 0\le r$ 时，先随机 $t=0$ 或 $1$ 来确定符号。
  • 当 $t=0$ 时，输出 -，生成 $[0,|l|]$ 的整数。
  • 当 $t=1$ 时，生成 $[0,r]$ 的整数。
• 当 $0\le l\le r$ 时，直接生成 $[l,r]$ 的整数。

注意以上操作中输出 -0 的情况要处理一下。
示例代码：

#include
using namespace std;

int main()
{
	srand(time(0)); 
	int n,l,r;
	cin>>n>>l>>r;
	while(n--)
	{
		if(l<=r&&r<=0)
		{
			int d=rand()%(abs(l)-abs(r)+1)+abs(r);
			if(d) cout<<'-';//防止 -0
			cout<<d;
		}
		else if(l<=0&&0<=r)
		{
			int f=rand()%2;
			if(f) cout<<rand()%(r+1);
			else
			{
				int d=rand()%(abs(l)+1);
				if(d) cout<<'-';//防止 -0
				cout<<d;
			}
		}
		else cout<<rand()%(r-l+1)+l;
		puts(""); 
	}
 	return 0;
}

效果：

---

6. 后记

那这次的介绍到尾声了。有很多像模拟退火、随机调整等随机化算法，在这里不再赘述，感兴趣的读者可以查阅相关资料学习一下。随机化是游戏中重要的操作之一，相信读者已经有所收获，点个赞或者关注我一下吧，谢谢！