BF算法和KMP算法

今天在课堂上老师讲了一道题：

我们假设有这么一段dna：abcabcabad

我们又假设有这么一段病毒： aba

我们需要在这段的那、中去找到这么一个病毒。

1.BF算法

那么我们一般会想到BF算法：

简单介绍一下BF算法

即暴力(BruteForce)算法，是普通的模式匹配算法，BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。BF算法是一种蛮力算法。

这种算法虽然很慢，但是很简单，很容易写。

BF算法思路：

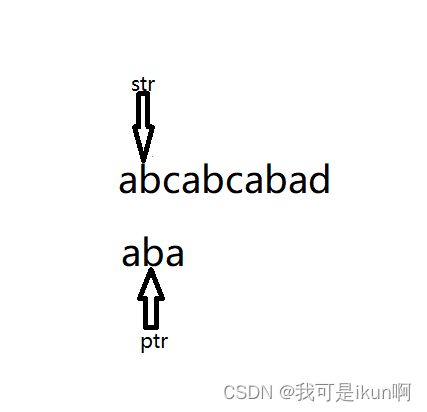
1 . 首先创建这两个指针 ，str表示我们要查找的整个字符串；ptr表示目标字符串。

2.  我们一步步的移动str，，每移动一次就与ptr对比，直到str与ptr第一位相同。

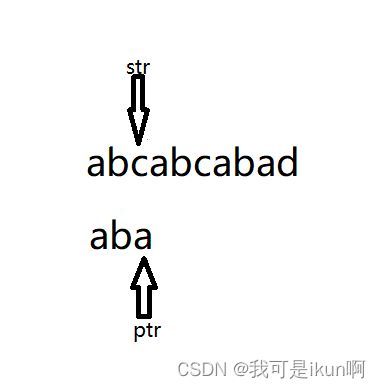
3.遇到str与ptr相等就同时向后移动同时，str与ptr继续比较。

 4. 如果ptr整个目标字符串都与str指向的字符串一一匹配，则说明已经找到我们所需要的目标。如果在接下来遇到的字符串不同，则需要回溯。

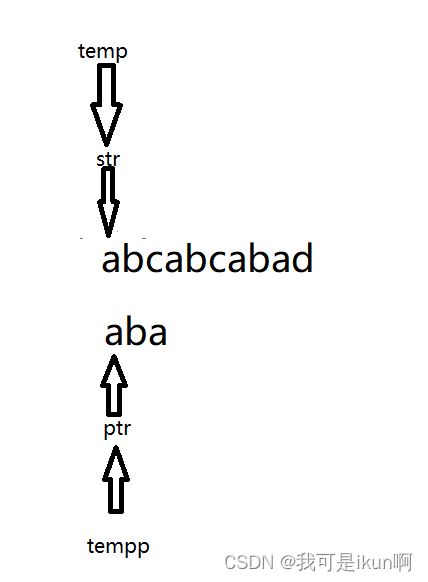
我们发现，第三个并不匹配，所以需要回溯，那么我们就需要用到第三个指针，回到从第一个开始匹配的指针的位置。这里用temp来记录第一次匹配的位置。同时，我们的ptr也需要回到最开始的位置，我们还需要tempp来记录最开始的位置。

这里其实可以选择移动str和ptr，然后用tempp和temp来保存位置，也可以反过来。

如图所示。

 5. 这时回溯后，str 继续向后移，直到再次与ptr匹配，temp 也随之记录，重复上述操作，直到找到，或者找不到。

代码实现：

#include 
#include 

void BF(char* str,char* ptr)
{
	assert(str != NULL && ptr != NULL);
	while (*str != '\0')//直到str找到末尾
	{
		char* temps = str;
		char* tempp = ptr;
		while (*tempp == *temps && *temps != '\0')
		{
			if (*tempp++ == *temps++)
			{
				; // 相互匹配则++
			}
			else
				break;
		}
		if (*tempp == '\0')
		{
			printf("找到了\n");
			return ;
		}
		str++;
	}
	printf("没找到\n");
}
int main()
{
	char* str = "adccscd";
	char* ptr = "cc";
	BF(str,ptr);
	return 0;
}

 这段代码，用暴力解法是可行的。

但是这样太慢了，如果数据一多，我的目标只是一小段，那么效果就非常不好，于是，我们有了KMP算法。

2. KMP算法

简单介绍一下KMP算法 ：KMP算法由D.E.Knuth，J.H.Morris和V.R.Pratt三位大神在1977年提出，它的核心算法是利用匹配失败后的信息，减少模式串与主串的匹配次数，以达到快速匹配的目的。

看不懂理论的可以去b站上看 “ 天勤率辉 ” 的动画演示，讲的非常清楚，非常得直观。

本图片来自：天勤考研。 

假设蓝色的主串，橙色为目标字符串。

箭头所指位置我们发现不匹配。

 但是我们发现箭头所指向之前的AB是可以匹配的，我们称之为模式串的公共前后缀。

这点就是我们KMP算法的核心算法：

 我们直接把前面相互匹配的移过来，使得公共前后缀的前缀移动公共前后缀的后缀。

这样我们就可以保证目标字符串和主串是相互匹配的。

 在举个例子：

我们字串去与主串匹配，我们找到了X与之不匹配于是乎：

 

从前面的前缀移动到了后缀。

 

我们在移动过程中不可以有这么一个位置：

 

将AB移动到这个位置，如果有那么

 这一段才是我们真正的公共前后缀，这里就引出了这样一个最长公公共前后缀的概念：

如果字串中有多对公共前后缀那么我们取最长的那一队。

我们继续最开始例子：继续扫描

 又发现了不匹配：

找出最长的公共前后缀

 移动主串：

 我们发现子串超出主串；可以判断匹配失败。

可以看出这个效率比BF算法高得多。

next数组：

我们创建一个next数组，长度为字串的长度 + 1：

 j 是 next 数组下表，我们j = 0是可以放 -1 ，也可以是 0 。

因为一般我们都是像上图一般把模式串也就是子串的第一个放入对应的下表处，

再去比较模式串中的字符 和 模式串前面的字符。

我们next记录的是改下表之前所匹配的个数，所以 j = 1 时，前面没有元素，必然next[ 1 ] = 0；

到第二个时，我们如果发现前面的模式串与前面的字符可以匹配，则记录1，否则还是0；

到第三个时，我们如果发现前面的模式串与前面的字符可以完全匹配，记录2，否则如果第一个匹配一个则记录为1；全都不匹配则为0。

后面的以此类推。

 也可以这样写：

 拿这个举例：为什么  i 下表下a = 3 ;

 

假设 next[ i ] = k;

那么我们可以推导出： p[ 0 ]  ~p[ k - 1 ] = p [ x ] ~ p [ i - 1 ]成立。

这里的x是不确定的；进一步推导出：那么我们在向后移动一个就可以推导出：

那么我就推导出最终的结果： next[ i +1 ] = k +1 ;  

 如果不理解的话，可以去b站听老师讲课，链接如下：【完整版】终于有人讲清楚了KMP算法，Java语言C语言实现_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1UL411E7M8/?spm_id_from=333.337.search-card.all.click&vd_source=93857e709631270a9e771d5aaee79ecb

#include 
#include 
#include 
#include 

void GetNext(char* sub, int* next, int lenSub)
{
	next[0] = -1;
	next[1] = 0;
	int i = 2;//当前该下标
	int k = 0;//前一个匹配过的个数
	while (i < lenSub)
	{
		if (k == -1 || sub[i - 1] == sub[k])
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else
			k = next[k];
	}
}

int KMP(char* str,char* sub,int pos)
{
	assert(str != NULL && sub != NULL);
	int lenStr = (int)strlen(str);
	int lenSub = (int)strlen(sub);
	if (lenStr == 0 || lenSub == 0)
		return -1;
	if (pos < 0 || pos >= lenStr)
		return -1;

	int i = pos; //遍历主串
	int j = 0;//遍历子串
	int* next = (int*)malloc(sizeof(int) * lenSub);
	assert(next != NULL);
	GetNext(sub,next,lenSub);
	while (i = lenSub)
	{
		return i - j;
	}
	return -1;
}

int main()
{
	printf("%d", KMP("abbbac", "bac", 0));
	return 0;
}