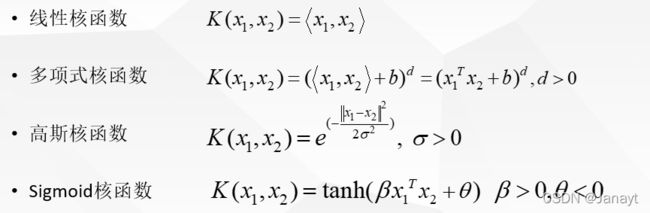Task02——支持向量机(Support Vector Machine,SVM)
支持向量机(Support Vector Machine,SVM)
本系列是2022年12月DataWhale组队学习中sklearn机器学习实战中的第二个学习任务——SVM,开源的在线学习地址 ,下面我们就开始本次学习之旅了!
支持向量机,英文名称Support Vector Machine,简称SVM,他是监督学习的一种,被广泛应用于统计分类以及回归分析中。它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。SVM是一种对线性和非线性数据分类的方法,使用一种非线性映射,把原始训练数据映射到较高维上,在新的维上,它搜索最佳的分割超平面(即将一个类的数据与其他类分离的“决策边界”)。它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中。支持向量机方法是建立在统计学习理论和VC维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定样本的学习精度)和学习能力之间寻求最佳折衷,以期获得最好的推广能力(泛化能力)。
所谓VC维是对函数类的一种度量,可以简单理解为问题的复杂程度,VC维越高,一个问题就越复杂,正是因为SVM关注的是VC维,后面我们可以看到,SVM解决问题的时候,和样本的维数是无关的(甚至样本维度是上万维的都可以)。
那什么是结构风险最小呢?机器学习的本质是对一种问题真实模型的逼近(我们选择一个我们认为比较好的近似模型,这个近似模型就叫一个假设),但毫无疑问,真实模型一定是不知道的。既然真实模型不知道,那我们选择假设问题与问题真实解之间有多大的差距,我们就没法得知。这个与问题真实解之间的误差,叫做风险(更严格的说,误差的累积叫做风险)。我们选择一个假设之后(更直观的说,我们得到了一个分类器之后),真实误差无从得知,但我们可以用某些可以掌握的量来逼近它。最直观的想法就是使用分类器在样本数据上的分类结果与真实结果之间的差值来表示,这个差值叫做经验风险。以前的机器学习方法都把经验风险最小化作为努力的目标,但后来发现很多分类函数能够在样本集上轻易达到100%的正确率,在真实分类任务中却一塌糊涂(即所谓的泛化能力)。此时的情况便是选择了一个足够复杂的分类函数(因为它的VC维很高),能够精确的记住每一个样本,但对样本之外的数据一律分类错误,回头看看经验风险最小化原则我们就会发现,此原则适用的大前提是经验风险确实能够逼近真实风险才行(一致),但实际上能逼近吗?答案是不能。因为样本数相对于现实世界要分类的文本数来说简直是九牛一毛,经验风险最小化原则只在着占很小比例的样本上做到没有误差,当然不能保证在更大比例的真实文本上也没有误差。
统计学因此而引入了泛化误差的概念,就是指真实风险应该由两部分内容刻画,一是经验风险,代表了分类器在给定样本上的误差;二是置信风险,代表了我们在多大程度上可以信任分类器在未知文本上的分类结果。很显然,第二部分是没有办法精确计算的,因此只能给出一个估计区间,也使得整个整个误差只能计算上界,而无法计算准确的值。
置信风险与两个量有关,一是样本数量,显然给定的样本数量越大,我们的学习结果越有可能正确,此时置信风险越小;二是分类函数的VC维,显然VC维越大,推广能力越差,置信风险会变大。
泛化误差界的公式为:
R(w) <= Remp(w)+Ф(n/h)
公式中R(w)就是真实风险,Remp(w)就是经验风险,Ф(n/h)就是置信风险。统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小,即结构风险最小。而SVM正是这样一种努力最小化结构风险的算法。
线性分类器
说起线性分类器,首先得说分类器的起源,Logistic回归。
逻辑回归的Sigmoid函数为
h ( z ) = 1 1 + e − z h(z) = \frac{1}{1+e^{-z}} h(z)=1+e−z1
而
z = w T + b z=w^T+b z=wT+b
逻辑回归通过训练数据得到w和b
支持向量机

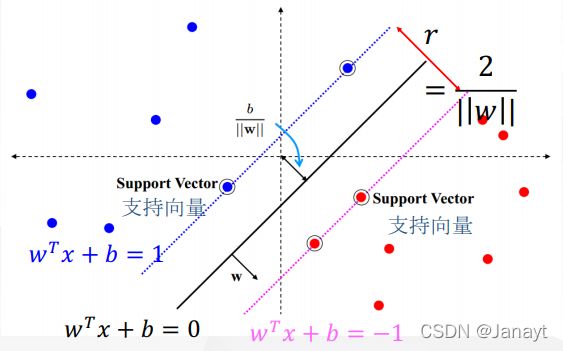
支持向量机要做的就是,我要画一条线,也就是一个分类器,让离这条线最近的红色的这些点到这条线的距离,和蓝色的点到这条线的距离最大。这就是支持向量机的核心思想:也就是最大化间隔。
支持向量机A是由支持向量决定的。因为假设在红色点的很上面,有一个点,他对支持向量机没有任何影响。
这背后有一套非常深的数学理论。我们一步一步解开他的庐山真面目。

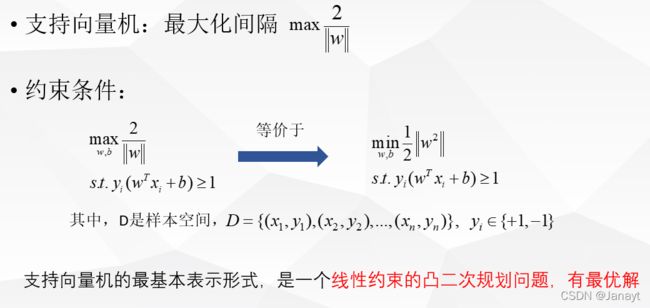



由于此问题的特殊结构,可以通过拉格朗日对偶性变换到对偶变量的优化问题,也就是通过与原问题等价的对偶问题得到原始问题的最优解。这样做的优点:
-
对偶问题往往更容易求解。
-
可以自然的引入核函数,从而推广到非线性分类问题中。
-
那么什么是拉格朗日对偶性呢?拉格朗日乘子法怎么实现
简单来讲,就是给每个约束条件加上一个拉格朗日乘子 λ \lambda λ,定义拉格朗日函数。通过拉格朗日函数将约束条件融合到目标函数里去,从而只用一个函数表达式便能清楚的表达出我们的问题。
L ( w , b , λ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m λ i ( 1 − y i ( w T x + b ) ) \mathcal{L}(w,b,\lambda)=\frac{1}{2}||w||^2+\sum^m_{i=1}\lambda_i\left(1-y_i\left(w^Tx+b\right)\right) L(w,b,λ)=21∣∣w∣∣2+i=1∑mλi(1−yi(wTx+b))
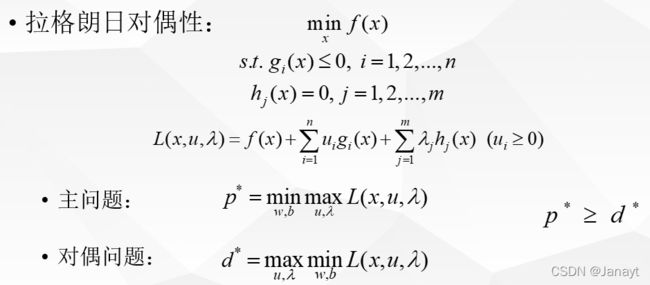
即对偶问题的最优解是原始主问题最优解的下界,并且在满足某些条件的情况下,这两者是相等的。因此可以通过求解对偶问题间接的求解原始问题。


此时的拉格朗日函数只包含了一个变量λ,然后第二步,对λ求极大值
利用SMO算法求解对偶问题中的λ。
核函数(Kernel)
-
到此为止,我们的SVM只能够处理线性分类问题,下面引入核函数的概念,进而推广到非线性分类问题。
-
而对于非线性的情况:
- 原始的方法:在用线性学习器学习一个非线性分类边界时,需要选择一个非线性的特征集的映射,然后将原始样本数据从低维映射成新的高维的特征空间中,在特征空间中使用线性分类器进行学习。
- SVM 的处理方法:选择一个核函数 K(·, ·) ,通过将数据从低维空间映射到高维空间,来解决在原始低维空间中线性不可分的问题。
我们先来看一个视频
我们可以看到,在二维平面中,有红色的点和蓝色的点,蓝色的点被一个圆圈分割开来,在二维平面中,我们很难线性的划分出一条边界,将两种颜色的点分隔开
核函数的做法是,将这些二维平面上的点映射到三维空间中,然后再三维空间中画一个平面,
意义在于,二维的时候,没办法做一个线性的切割,但是映射到三维后,核函数可以做一个平面切割,
在三维中,平面切割仍然是一个线性的。因此在高维的时候,这仍然是一个线性的问题。这就是核函数最强大的地方。

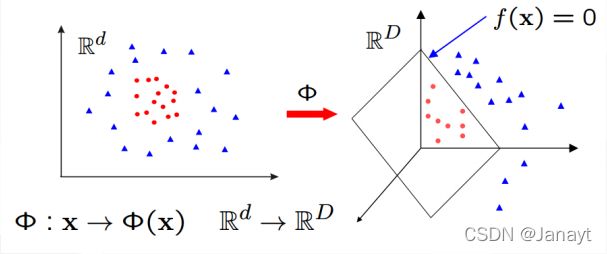

我不需要知道f是什么,我只需要知道核函数K是什么,我不需要知道怎么把二维映射成三维,每个点的具体是怎么表示的,这是一个显式的映射函数,但是SVM不需要知道,这个显式的映射函数是什么,我只需要知道这两个映射完之后,乘积是什么。
我不需要计算映射函数的线性表达式,我只需要知道结果。也就是说,我不需要知道在原来的空间对xi,xj做一些计算。
比如这是一个多项式的核,我只需要在原来的样本空间做内积就可以了
正则化和软间隔
当C越大,代表着分错的距离越来越窄,当C无穷大时,也就相当于没有分错,变成了硬间隔。
引入了正则化之后的拉格朗日函数如下,其后的求解过程与前述大致相似,再次就不在重复。
总结
- 优点:
- 解决高维特征的分类问题和回归问题很有效,在特征维度大于样本数时依然有很好的效果
- 稀疏性:仅仅使用支持向量来做超平面的决策,无需依赖全部数据
- 核函数可以很灵活的来解决各种非线性的分类回归问题
- 样本量不是海量数据的时候,分类准确率高,泛化能力强
- 缺点:
- 如果特征维度远远大于样本数,则SVM表现一般
- SVM在样本量非常大,核函数映射维度非常高时,计算量过大,不太适合使用
- SVM对缺失数据敏感
用sklearn代码实现SVM
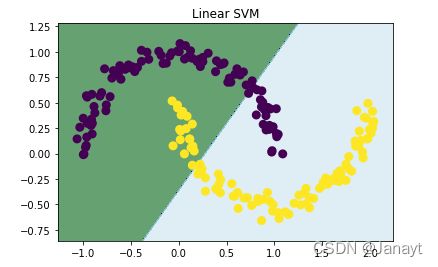
线性SVM
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_moons
x, y = make_moons(n_samples=200, shuffle=True, noise=0.06, random_state=None)
x_min, x_max = x[:, 0].min() - 0.2, x[:, 0].max() + 0.2
y_min, y_max = x[:, 1].min() - 0.2, x[:, 1].max() + 0.2
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.002),
np.arange(y_min, y_max, 0.002)) # meshgrid如何生成网格
model_linear = svm.SVC(kernel='linear', C = 0.001)
model_linear.fit(x, y) # 训练
Z = model_linear.predict(np.c_[xx.ravel(), yy.ravel()]) # 预测
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap = plt.cm.ocean, alpha=0.6)
plt.scatter(x[:, 0], x[:, 1], marker='o', c=y, lw=3)
# plt.scatter(x[:, 0], x[:, 1], marker='x', color='k', s=100, lw=3)
plt.title('Linear SVM')
plt.show()
plt.figure(figsize=(16, 15))
for i, degree in enumerate([1, 3, 5, 7, 9, 12]):
# C: 惩罚系数,gamma: 高斯核的系数
model_poly = svm.SVC(C=0.0001, kernel='poly', degree=degree) # 多项式核
model_poly.fit(x, y)
# ravel - flatten
# c_ - vstack
# 把后面两个压扁之后变成了x1和x2,然后进行判断,得到结果在压缩成一个矩形
Z = model_poly.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.subplot(3, 2, i + 1)
plt.subplots_adjust(wspace=0.4, hspace=0.4)
plt.contourf(xx, yy, Z, cmap=plt.cm.ocean, alpha=0.6)
# 画出训练点
plt.scatter(x[:, 0], x[:, 1], marker='o', c=y, lw=3)
plt.title('Poly SVM with $\degree=$' + str(degree))
plt.show()
高斯核SVM
plt.figure(figsize=(16, 15))
for i, gamma in enumerate([1, 5, 15, 35, 45, 55]):
# C: 惩罚系数,gamma: 高斯核的系数
model_rbf = svm.SVC(kernel='rbf', gamma=gamma, C= 0.0001).fit(x, y)
# ravel - flatten
# c_ - vstack
# 把后面两个压扁之后变成了x1和x2,然后进行判断,得到结果在压缩成一个矩形
Z = model_rbf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.subplot(3, 2, i + 1)
plt.subplots_adjust(wspace=0.4, hspace=0.4)
plt.contourf(xx, yy, Z, cmap=plt.cm.ocean, alpha=0.6)
# 画出训练点
plt.scatter(x[:, 0], x[:, 1], marker='o', c=y, lw=3)
plt.title('RBF SVM with $\gamma=$' + str(gamma))
plt.show()
测试不同SVM在Mnist数据集上的分类效果
# 添加目录到系统路径方便导入模块,该项目的根目录为".../machine-learning-toy-code"
import sys
from pathlib import Path
curr_path = str(Path().absolute())
parent_path = str(Path().absolute().parent)
p_parent_path = str(Path().absolute().parent.parent)
sys.path.append(p_parent_path)
print(f"主目录为:{p_parent_path}")
from torch.utils.data import DataLoader
from torchvision import datasets
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
train_dataset = datasets.MNIST(root = p_parent_path+'/datasets/', train = True,transform = transforms.ToTensor(), download = False)
test_dataset = datasets.MNIST(root = p_parent_path+'/datasets/', train = False,
transform = transforms.ToTensor(), download = False)
batch_size = len(train_dataset) # batch_size等于len(train_dataset),即一次性读取整个数据集
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=True)
X_train,y_train = next(iter(train_loader))
X_test,y_test = next(iter(test_loader))
X_train,y_train = X_train.cpu().numpy(),y_train.cpu().numpy() # tensor转为array形式)
X_test,y_test = X_test.cpu().numpy(),y_test.cpu().numpy() # tensor转为array形式)
X_train = X_train.reshape(X_train.shape[0],784)
X_test = X_test.reshape(X_test.shape[0],784)
# 截取部分数据,否则程序运行可能超时
X_train, y_train= X_train[:2000], y_train[:2000]
X_test, y_test = X_test[:200],y_test[:200]
# C:软间隔惩罚系数
C_linear = 100
model_linear = svm.SVC(C = C_linear, kernel='linear').fit(X_train,y_train) # 线性核
print(f"Linear Kernel 's score: {model_linear.score(X_test,y_test)}")
for degree in range(1,10,2):
model_poly = svm.SVC(C=100, kernel='poly', degree=degree).fit(X_train,y_train) # 多项式核
print(f"Polynomial Kernel with Degree = {degree} 's score: {model_poly.score(X_test,y_test)}")
for gamma in range(1,10,2):
gamma = round(0.01 * gamma,3)
model_rbf = svm.SVC(C = 100, kernel='rbf', gamma = gamma).fit(X_train,y_train) # 高斯核
print(f"Polynomial Kernel with Gamma = {gamma} 's score: {model_rbf.score(X_test,y_test)}")
参考文献
[1] 嘉士伯的Java小屋
[2] 支持向量机通俗导论——理解 SVM的三层境界,July