Python 图像处理基础 || 图像的空域与频域

图像的空域与频域

1. 一维信号的空域域频域

一维空域信号的属性

$f(x)=A\cdot \text{sin}(w\cdot x)$

其中，$A$ 称为信号的幅值，$w$ 称为信号的频率

信号的频率代表了细节的多少，频率越高，细节越多；幅值代表了信号中值的大小。

import numpy as np
import matplotlib.pyplot as plt

A1 = 2
A2 = 5
w1 = 3
w2 = 6
x = np.arange(0,5,0.01)
y1 = A1*np.sin(w1*x)
y2 = A2*np.sin(w2*x)

plt.subplot(2,1,1),plt.plot(x,y1)
plt.subplot(2,1,2),plt.plot(x,y2)
plt.show()

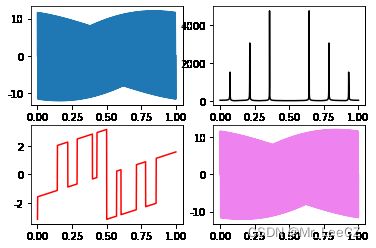
傅里叶变换可以显示出信号的高频和低频部分，将信号的频率和相位展示出来，并且可以进行无损还原

import numpy as np
from scipy.fftpack import fft,ifft,fftshift
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
 
#采样点选择1400个，因为设置的信号频率分量最高为600赫兹，根据采样定理知采样频率要大于信号频率2倍，所以这里设置采样频率为1400赫兹（即一秒内有1400个采样点，一样意思的）
x=np.linspace(0,1,1400)      
 
#设置需要采样的信号，频率分量有200，400和600
y=7*np.sin(2*np.pi*200*x) + 5*np.sin(2*np.pi*400*x)+3*np.sin(2*np.pi*600*x)
 
fft_y=fft(y)                          #快速傅里叶变换
 
abs_y=np.abs(fftshift(fft_y))                # 取复数的绝对值，即复数的模(双边频谱)
angle_y=np.angle(fft_y)            #取复数的角度
y_ = ifft(fft_y)
 
plt.subplot(221)
plt.plot(x,y)   
 
plt.subplot(222)
plt.plot(x,abs_y,'black')

 
plt.subplot(223)
plt.plot(x,angle_y,'r') 
 
plt.subplot(224)
plt.plot(x,y_,'violet')
 
plt.show()

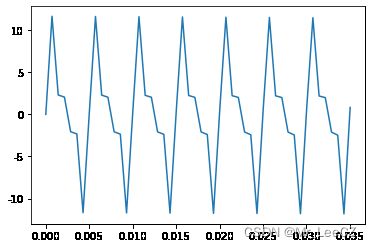
plt.figure()
plt.plot(x[0:50],y[0:50])   
plt.show()

2. 图像的空域与频域

图像中的任意一行（或者列）是一个一维信号，因此，图像也是一种信号。

import matplotlib.pylab as plt
import matplotlib.image as mpimg

im = mpimg.imread("images/parrot.png")
print(im.shape,im.dtype,type(im))#  读入的图像包含R、G、B、alpha 四个通道，可通过 convert 进行其它格式的转换不能直接imshow输出
plt.figure(figsize=(10,10))
plt.imshow(im)
plt.axis('off')
plt.show()

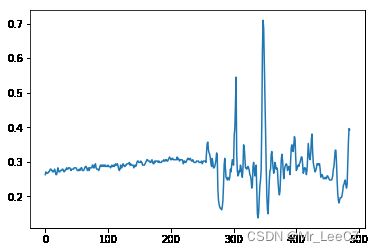
图像的一行就是一个一维信号，天空颜色变化平缓，代表了低频部分；植物叶子像素值变化剧烈，代表着高频区域。

vect = im[5,:,0]
plt.plot(vect)
plt.show()

3. 图像傅里叶变换后的频谱图与相位图

图像的傅里叶变换会分离出图像的频谱图和相位图两类图像，频谱图的低频部分分布在频率图像的四个角，高频部分分布在图像的中间。频谱图像亮度较高表示图像的低频部分数量较多，做shift变换是通过平移对角区域的方式将低频信息居中。反傅里叶变换可直接对傅里叶变换的结果进行操作，也可以对傅里叶变换后的结果进行shift变换，然后再做反傅里叶变换。

import numpy as np
from skimage.io import imread
from skimage.color import rgb2gray
import numpy.fft as fp
import matplotlib.pyplot as plt

im = rgb2gray(imread('images/house.png'))
freq = fp.fft2(im) # 复数结构的矩阵，其中包含了频率、幅值和相位

plt.imshow(im,cmap='gray')
plt.axis('off')
plt.show()

plt.imshow(20*np.log10(0.01+np.abs(freq)),cmap='gray')
plt.axis('off')
plt.show()

plt.imshow(np.angle(freq),cmap='gray')
plt.axis('off')
plt.show()

plt.imshow(20*np.log10(0.01+np.abs(fp.fftshift(freq))),cmap='gray')
plt.axis('off')
plt.show()

plt.imshow(np.angle(fp.fftshift(freq)),cmap='gray')
plt.axis('off')
plt.show()

4. 图像的二维傅里叶变换案例

import numpy as np
from skimage.io import imread
from skimage.color import rgb2gray
import numpy.fft as fp

im = rgb2gray(imread('images/house.png'))
plt.figure(figsize=(12,10))
freq = fp.fft2(im) # 复数结构的矩阵，其中包含了频率、幅值和相位
im_ = fp.ifft2(freq).real
plt.subplot(2,2,1),plt.imshow(im,cmap='gray')
plt.subplot(2,2,2),plt.imshow(20*np.log10(0.01+np.abs(fp.fftshift(freq))),cmap='gray')
plt.subplot(2,2,3),plt.imshow(np.angle(fp.fftshift(freq)),cmap='gray')
plt.subplot(2,2,4),plt.imshow(np.clip(im_,0,255),cmap='gray')
plt.show()