【算法复杂度——空间复杂度-Python】算法空间复杂度的详细介绍

上一篇博客中我们学习了时间复杂度：需要的小伙伴请点击：

https://blog.csdn.net/qq_43355165/article/details/122644530

概念定义

空间复杂度涉及的空间类型有：

• 输入空间：存储输入数据所需的空间大小；
• 暂存空间： 算法运行过程中，存储所有中间变量和对象等数据所需的空间大小；
• 输出空间： 算法运行返回时，存储输出数据所需的空间大小；
  通常情况下，空间复杂度指在输入数据大小为N时，算法运行所使用的暂存空间 + 输出空间的总体大小。
  
  而根据不同来源，算法使用的内存空间分为三类：

指令空间：

编译后，程序指令所使用的内存空间。

数据空间：

算法中的各项变量使用，包括：声明的变量、变量、动态数组、动态对象等使用的内存空间。

class Node:
	def __init__(self, val):
		self.val = val
		self.next = None
	def algorithm(N):
		num = N        # 数组
		nums = [0] * N # 动态数组
		node = Node(N) # 动态对象

栈帧空间：

程序调用函数是基于栈实现的，函数在调用期间，占用常量大小的栈帧空间，直至返回后释放。如以下代码所示，在循环中调用函数，每轮调用test()返回后，栈帧空间已被释放，因此空间复杂度仍为O(1)。

def test():
	return 0
def algorithm(N):
	for _ in range(N):
		test()

算法中，栈帧空间的累计常出现于递归调用。如以下代码所示，通过递归调用，会同时存在N个未返回的函数 algorithm()，此时累计使用O(N)大小的栈帧空间。

def algorithm(N):
	if N <= 1: return 1
	return algorithm(N - 1) + 1

符号表示

通常情况下，空间复杂度统计算法在“最差情况”下使用的空间大小，以体现算法运行所需预留的空间量，使用符号O表示。
最差情况有两层含义，分别为最差输入数据、算法运行中的最差运行点。例如以下代码：

• 最差输入数据：当N<=10时，数组nums的长度恒定为10，空间复杂度为O(10) = O(1)；当N > 10时，数组nums长度为N，空间复杂度为O(N)；因此，空间复杂度应为最差输入数据情况下的O(N)。
• 最差运行点：在执行nums = [0] * 10时，算法仅使用O(1)大小的空间；而当执行nums = [0] * N时，算法使用O (N)的空间；因此，空间复杂度应为最差运行点的O(N)。

def algorithm(N):
	num = 5			   # O(1)
	nums = [0] * 10    # O(1)
	if N > 10:
	 	nums = [0] * N # O(N)

常见种类

根据从小到大排列，常见的算法空间复杂度有：
O(1) < O(logN) < O(N) < O(N ²) < O(2^N)

示例解析

对于以下所有示例，设输入数据大小为正整数N，节点类Node、函数test()如以下代码所示。

class Node:
	def __init__(self, val):
		self.val = val
		self.next = Node
	# 函数 test()
def test():
	return 0

常数O(1):

普通常量、变量、对象、元素数量与输入数据大小N无关的集合，皆使用常数大小的空间。

def algorithm(N):
	num = 0
	nums = [0] * 10000
	node = Node(0)
	dic = {0: '0'}

如以下代码所示，虽然函数test()调用了N次，但每轮调用后test()已返回，无累计栈帧空间使用，因此空间复杂度仍为O(1)。

def algorithm(N)
	for _ in range(N):
		test()

线性O(N)

元素数量与N呈线性关系的任意类型集合（常见于一维数组、链表、哈希表等），皆使用线性大小的空间。

def algorithm(N):
	nums_1 = [0] * N
	nums_2 = [0] * (N // 2)

	nodes = [Node(i) for i in range(N)]
	
	dic = {}
	for i in range(N):
		dic[i] = str(i)

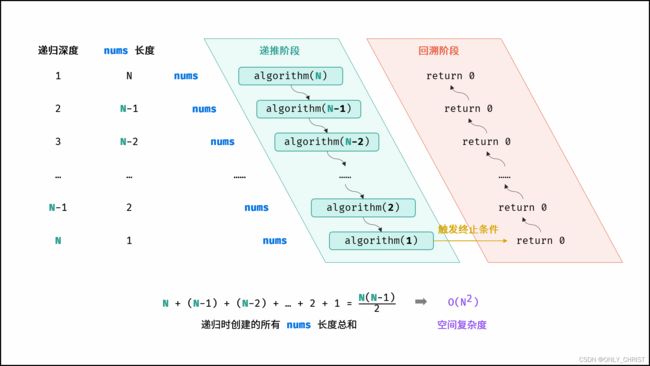
如下图与代码所示，此递归调用期间，会同时存在N个未返回的algorithm()函数，因此使用O(N)大小的栈帧空间。

def algorithm(N):
	if N <= 1: return 1
	return algorithm(N - 1) + 1

平方O(N²)：

元素数量与N呈平方关系的任意类型集合（常见于矩阵），皆使用平方大小的空间。

def algorithm(N):
	num_matrix = [[0 for j in range(N)] for i in range(i)]
	node_matrix = [[Node(j) for j in range(N)] for i in range(N)]

如下图与代码所示，递归调用时同时存在 N 个未返回的algorithm()函数，使用 O(N) 栈帧空间；每层递归函数中声明了数组，平均长度为N/2 ，使用 O(N)空间；因此总体空间复杂度为 O(N²)。

def algorithm(N):
    if N <= 0: return 0
    nums = [0] * N      # O(N)
    return algorithm(N - 1)

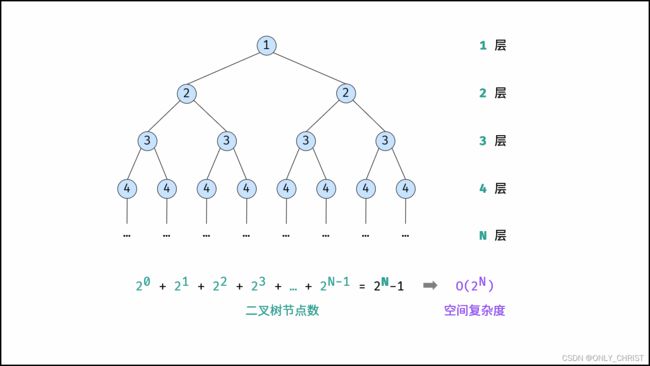
指数O(2^N) ：

指数阶常见于二叉树、多叉树。例如，高度为N的满二叉树的节点数量为2^N，占用O(2^N)大小的空间；同理，高度为N的满m叉树的节点数量为m^N，占用O(m^N) = O(2^N)大小的空间。

对数O(logN) ：

对数阶常出现于分治算法的栈帧空间累计、数据类型转换等，例如：

• 快速排序 ，平均空间复杂度为 Θ(logN) ，最差空间复杂度为 O(N) 。拓展知识：通过应用 Tail Call Optimization ，可以将快速排序的最差空间复杂度限定至O(N) 。
• 数字转化为字符串 ，设某正整数为 N ，则字符串的空间复杂度为 O(logN) 。推导如下：正整数 N 的位数为 log₁₀N ，即转化的字符串长度为log₁₀N，因此空间复杂度为 O(logN) 。

时空权衡

对于算法的性能，需要从时间和空间的使用情况来综合评价。优良的算法应具备两个特性，即时间和空间复杂度皆较低。而实际上，对于某个算法问题，同时优化时间复杂度和空间复杂度是非常困难的。降低时间复杂度，往往是以提升空间复杂度为代价的，反之亦然。

由于当代计算机的内存充足，通常情况下，算法设计中一般会采取「空间换时间」的做法，即牺牲部分计算机存储空间，来提升算法的运行速度。

以 LeetCode 全站第一题 两数之和 为例，「暴力枚举」和「辅助哈希表」分别为「空间最优」和「时间最优」的两种算法。

方法一：暴力枚举

时间复杂度 O(N²) ，空间复杂度O(1) ；属于「时间换空间」，虽然仅使用常数大小的额外空间，但运行速度过慢。

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i in range(len(nums) - 1):
            for j in range(i + 1, len(nums)):
                if nums[i] + nums[j] == target:
                    return i, j
        return

方法二：辅助哈希表

时间复杂度 O(N)，空间复杂度 O(N)；属于「空间换时间」，借助辅助哈希表 dic ，通过保存数组元素值与索引的映射来提升算法运行效率，是本题的最佳解法。

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        dic = {}
        for i in range(len(nums)):
            if target - nums[i] in dic:
                return dic[target - nums[i]], i
            dic[nums[i]] = i
        return []

在 LeetCode 题目中，「输入空间」和「输出空间」往往是固定的，是必须使用的内存空间。因希望专注于算法性能对比，本 LeetBook 的题目解析的空间复杂度仅统计「暂存空间」大小。

本文转自：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/r8ytog/