肝进ICU,万字真言点化八大排序——我奶奶都看得懂的算法详解
目录
-
- 传统艺能
- 排序应用
- 插入排序
- 冒泡排序
- 希尔排序
-
- 预排序
- 堆排序
- 选择排序
- 快速排序
-
- hoare 法
- 挖坑法
- 前后指针法
- 取中优化
- 小区间优化
- 非递归快排
- 归并排序
-
- 非递归归并
- 各类算法复杂度比较
传统艺能
小编是双非本科大一菜鸟不赘述,欢迎米娜桑来指点江山哦(QQ:1319365055)
非科班转码社区诚邀您入驻
小伙伴们,打码路上一路向北,彼岸之前皆是疾苦
一个人的单打独斗不如一群人的砥砺前行
这是我和梦想合伙人组建的社区,诚邀各位有志之士的加入!!
社区用户好文均加精(“标兵”文章字数2000+加精,“达人”文章字数1500+加精)
直达: 社区链接点我
排序应用
在这个功利的时代,生活中无时无刻都充斥着各种排序,这背后赋予排序价值的是我们对这些东西的价值评估,随便点开一个网站,不管是新闻,购物还是娱乐,都会有大大小小的排名,所以也并不陌生。
正因为排序有实在太多的运用,所以我们的先辈在排序上也是深有研究,搞出了很多种类的排序:

上面有些排序我们之前已经见识了,在面对同一个场景时,他们的执行情况可谓是天差地别。
插入排序
插入排序是比较简单的一种排序,有多简单呢就好像你斗地主,拿到牌后自己理牌让你手上的牌有一个从小到大或从大到小的顺序,当然如果你说你没打过牌,或者打牌从不理牌那就当我没说
所以插入排序的基本思想就是往一个有序区间插入一个数据,依旧保持他有序。

代码表示就是:
void Insertion(int* a,int n)
{
int end;
int tem = a[end+1];
while(end>=0 && end<n-2)
{
if(tem<a[end])
{
a[end+1] = a[end];
end--;
}
else
{
break;
}
}
a[end+1] = tem;//放外面可以同时处理end为-1的情况
}
冒泡排序时间复杂度最差为 : O(N^2) ,最好为O(N)
冒泡排序
冒泡排序一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。
因为我们老早就研究过了,不赘述上代码:
void Bubble(int* a,int n)
{
for(int i =0;i<n;i++)
{
for(int j = 1;j<n-i;j++)
{
if(a[j-1]>a[j])
{
Swap(&a[j-1],&a[j]);//交换函数
}
}
}
}
冒泡排序时间复杂度为 : O(N^2) ,还有一种优化算法,就是立一个 flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序。但这种改进对于提升性能来冒泡排序说并没有什么太大作用。
int flag = 0;
if(a[j-1]>a[j])
{
flag = 1;
Swap(&a[j-1],&a[j]);//交换函数
}
if(flag == 0)
{
break;
}
你可能会觉得插入排序和冒泡排序时间复杂度是一样的,所以他们效率一样好,那你就错了。
在完全有序的情况下,两者的效率是一样的,但是在接近于有序的时候就要具体分析了。
希尔排序
希尔提出的希尔排序也称为递减增量算法,他的本质是插入排序的优化算法,插入排序在对几乎已经排好序的数据操作时,效率高,但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位,这就是希尔排序所做出的优化。
希尔排序包括预排序和直接插入排序
希尔排序的思路是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序
预排序
预排序即为分组排,目的是让整个序列先接近于有序。
这若干个子序列如何来分呢?我们引入一个间隔变量 gap ,即间隔大小为 gap 的元素分为一组,gap 越小越接近于有序, gap 越大,大的数据就越快到后面,小的数据就越快到前面。
void Shell(int* a,int n)
{
int end;
int gap = 3;
int tem = a[end+gap];
for(int i = 0;i<gap;i++)//组数次排序
{
for(int j = i;j < n-gap;j += gap)//单组排序
{
while(end>=0)//组内对象操作
{
if(tem<a[end])
{
a[end+gap] =a[end];
end -= gap;
}
else
{
break;
}
}
a[end+gap] = tmp;
}
}
}
这是传统思路的三层循环,我们可以做优化,最终变成两层循环:我们操作每组的循环,不再让 i += gap,我们让他直接 ++,就意味着同时操作多组排序,此时我们假设 gap 为 n。
int gap = n;//gap要和n关联,可以多组预排序,n越大gap应该越大
while(gap>1)//=1的时候进行插入排序
{
gap = gap/3+1;//gap递减关系,保证最后一步进行插入排序
for(int i = 0;i < n-gap ;i++)
{
……
}
}
以上就是预排序,你可能会疑惑预排序是让他接近有序,并不是有序,过了还是得进行插入排序,到底有没有优化效果呢?
那我先马后炮一波,你想想要是他不快,那所谓八大排序他能榜上有名吗?

那我们以数据说话,以最坏的逆序来讲,每个数都得挪,但时间复杂度就基本为 O(N)了(希尔的时间复杂度炒鸡难算,很多地方都是直接给的结论:O(N^1.3)),因为足够大的时候里面那层循环可以忽略,接近 1 的时候已经接近有序了不管 gap 是大是小,都差不多为 O(N)。
既然如此就引出了希尔排序的致命弱点,当我本来为升序或降序时我去排升序和降序,虽然这样预排序的成本会减少,但预排序部分相当于就是纯纯多余白白浪费。

堆排序
堆排序这里不再赘述,前几天才发了堆排序的专题博客,链接:直接这里不迷路
选择排序
红花都是靠绿叶衬托出来的,其他的快速排序,堆排序,希尔排序之所以有优越性就是建立在与选择排序这类进行对比而得出来的。
选择排序是最基本的排序算法之一,因为无论什么数据进去都是 O(n²) 的时间复杂度,所以用到它的时候,数据规模越小越好,唯一的好处可能就是不占用额外的内存空间了吧。
直接选择排序思路是在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。重复直到所有元素均排序完毕。
代码如下:
void Select(int*a,int n)
{
int left = 0,right = n-1;
while(left<right)
{
int mina = left,maxa = left;
for(int i =left+1;i<=right;i++)
{
if(a[i]<a[mina])
{
mina = i;//找到最小值
}
if(a[i]>a[maxa])
{
maxa = i;//找到最大值
}
}
Swap(&a[left],&a[mina]);//进行交换
if(left==right)
maxa = mina;//处理mina与maxa重叠可能发生的数据调包
Swap(&a[right],&a[maxa]);
left++;
right--;
}
快速排序
大家可能久闻快排大名,qsort 可谓人尽皆知了,但不要以为快排就止步于 qsort 了,快排并不简单甚至有点复杂,原因就是快排的单趟排序部分变种很多,我们有必有去搞清楚他们的不同。
hoare 法
这个版本是发明快排的人搞出来的原始版本,所有变形版本都以他为基础。
单趟排序
选出一个标准,一般是第一个数或者最后一个,要求就是左值都比这个标准小,右值都比这个标准大。我们可以定义双指针,一个 left 找比标准大的,right 找比标准小的,找到就交换再继续,指针相遇时就和标准位置换。
我们标准位要和最小的交换才行,万一相遇位置的值比标准位大怎么办?不会的,因为很简单,我们以升序为标准算法会保证right 先走,相遇位置比标准位置小就两种情况,因为两个指针的相对移动是被动的,如果 right 找到比标准位小的,就让 left 去遇 right,left 停留位置必定小于标准位。否则如果 right 没有找到比标准小的,就直接去与 left 奔现,相遇位置也是比标准小的。
整体排序
和单趟排序一起,代码如下:
void Part(int* a,int left,int right)//单趟排序
{
int key = left;
while(left<right)
{
while(a[right]>=a[key] && left< right)//注意极端条件的控制
{
right--;//找小
}
while(a[left]<=a[key] && left< right)
{
left++;//找大
}
Swap(&a[left],&a[right]);
}
Swap(&a[key],&a[left]);
return left;
}
void Quick(int* a,int n)//整体排序
{
int key = Part(a,begin,end);
Quick(a,begin,key-1);
Quick(a,key+1,end);//递归+分治解决左右子问题
}
单趟排完了标准位已经排到了正确的位置,如果左边有序,右边有序,那整体就有序了,这时就可以利用分治解决子问题,比如这个场景:排序出序列【3,1,2,5,6,4】


这里拆分成 left ,right 属于一个递归的过程,也就是分成的子序列排序也会遵从这样的拆分排序,直到拆分到最小子序列(1个或0个),类似于我们之前二叉树的最小子问题为空树。具象出递归过程就是这样滴:
挖坑法
所谓的坑也就是一个标准位 key,可以是最左边也可以是最右边,我们将它保存起来,这是原来的地方就形成一个“ 坑位 ”,为什么说坑位,就是因为形成的位可以被覆盖,接下来坑位不动,假如 key 在最左边,另一端的指针就开始遍历寻找比 key 小的值,找到了就去覆盖坑位,然后自己再变成新的坑位,再次遍历左边开始,于是变成寻找比 key 大的值,去覆盖迭代,如此这般就能完成排序。
代码理解:
int PartHole(int* a, int left, int right)
{
if (a == NULL)
{
return NULL;
}
if (left >= right)
{
return;
}
int head = left;
int tail = right;
int key = left;
while (head < tail)
{
while(a[tail] >= a[key])
{
tail--;//右边找小
}
a[key] = a[tail];//占坑
while (a[head] <= a[key])
{
head++;//左边找大
}
}
a[key] = a[head];//占坑
return key;
}//挖坑法
那么这个方法相比 hoare 的优势就很明显了:
1. 不用理解为什么相遇位置比 key 小;
2. 不用理解为什么左边做 key,右边先走。

前后指针法
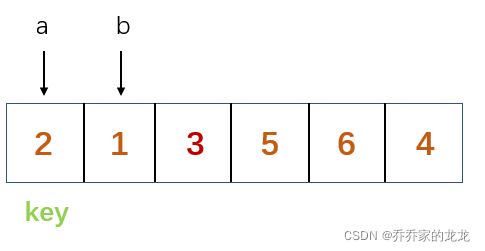
这里还是以升序为例,这个方法的核心就是保证prev指向及prev之前的所有数据的值都小于key。
- 当 b 还没遇见比 key 大的值的时候,a 是跟着 b 一起移动的。
- 当 b 第一次遇见比 key 大的值的时候,a 停下,此时 a 包括 a 之前的数据都是小于 key 的。
- 当 b 再一次遇见比 key 小的数据时,a 的下一个一定是比 key 大的数据,所以 a++ 和 b 交换。
- 直到遍历结束,a 之前包括 a 都比 key 小,key 和 a 交换。
- key 之前都比 key 小,key 之后都比 key 大。
然后我们来考虑一下key取最右边:
为了保证prev包括prev前的数据都是小于key的。 prev就不能从0位置开始了,万一第一个数就大于key呢?

接下来的路与取左边完全一样,直到cur在key位置的时候:同理,prev包括prev前的数据都是小于key的。
在左边的时候prev前面有key,所以可以直接交换。
在右边的时候直接交换会把小的数换到右边,所以交换的时候是换prev++的位置。
void Part(int* a,int left,int right)
{
if(a==NULL)
{
return NULL;
}
int prev = left;
int cur = left+1;
int key = left;
while(cur <= right)
{
if(a[key] > a[cur] && a[++prev]!=a[cur])//有点妙,细品一下前置++
{
prev++;//遇到比 key 小就++
Sawp(&a[cur],&a[prev]);//交换前后指针
}
cur++;
}
Swap(&a[prev],&a[key]);//交换标准位
return prev;
}
这就是快排的方法,那么快排都叫快排了他到底有夺快呢?
其实他的时间复杂度为:O(N*log N)
当然这是理想情况状态,key 为中位数,最坏情况是我们每次选的 key 是最大值或者最小值,其复杂度为O(N^2),这时快排不再快,而且还会有栈溢出风险!那我们有没有办法对最坏情况进行优化呢?

取中优化
在有序序列进行快排时,必定是复杂度最坏的情况,但是没有关系,我们针对 key 的选择做优化即可

我们可以随机选择一个 key,或者三数取中(第一个,最后一个以及第一个最后一个的中间一个),那为什么不是直接取中间值呢?因为如果是随机序列就不一定了,取中策略是针对有序序列,可以一把反转,将最坏情况秒变最好情况。随机序列随机取也不会影响效率,毕竟不可能每次都是最坏情况。
int Getmid(int* a,int left,int right)//三数取中需要两两比较,
//情况需要到位,因此过程有一点小繁琐
{
int mid = left+(right-left)/2;//防溢出
if(a[left]<a[mid])
{
else if(a[mid]<a[right])
{
return mid;
}
else if(a[left]>a[right])
{
return left;
}
else
{
return right;
}
}
else
{
if(a[left]>a[right])
{
return mid;
}
else if(a[left]<a[right])
{
return left;
}
else
{
return right;
}
}
}
void Part(int* a,int left,int right)
{
int mid = Getmid(a,left,right);
Swap(&a[left],&a[mid]);//三数取中
……
}
小区间优化
还有一种方法叫做小区间优化,很类似于一个递归调用的展开图,就是一棵二叉树,比如一个 1000 个元素的序列,就要走大概 10 层。key 在中间,比如 key 左边有 5 个数,要让这 5 个数的区间有序就需要 7 次递归,结论就是不划算。
我们对于数据量小的进行有序化,最理想的莫过于插入排序,递归展开的最后几层的数量是庞大的,但区间很小实际的递归价值非常小,因此我们直接采用插入排序替代原本的递归展开,所以小区间优化就是把大部分的调用消除掉,区间很小时可以不再使用递归划分的思路,而是直接使用插入排序对小区间排序。

实现:
void quick(int* a,int left,int right)
{
if(left <= right)//排除空序列和一个元素
return;
if(right - left+1 <= 10)
{
Insert(a+left,right-left+1);//插入排序实现小区间优化
}
else
{
int key = Part(a,left,right);
quick(a,left,key-1);
quick(a,key+1,right);//递归展开
}
}
这里的区间大小也是一个可以琢磨的地方,这里中肯的给了个 10,一般库里面给的区间大小为 13。

非递归快排
为什么要扯到非递归,很简单,这里再提一下操作系统的知识

系统中堆提供的大小几乎是栈的几百倍,栈的开销不仅仅给了函数的调用还要存局部变量和寄存器这些个玩意儿,而堆就只存我要做的处理,因此递归深度太深,栈他根本顶不住,所以非递归的场景就应运而生。
我们非递归实现原理是靠栈实现,但本质还是在模拟递归的过程:
void Quick(int* a, int head, int tail)
{
stack st;
init(&st);//初始化栈
push(&st, head);
push(&st, tail);//入序列首位的下标
while (!empty(&st))
{
int right = stacktop(&st);
pop(&st);
int left = stacktop(&st);
pop(&st);
int key = Part(a, left, right);//单趟排序
if (left < key - 1)
{
push(&st, left);
push(&st, key - 1);
}//左区间找key
if (key + 1 < right)
{
push(&st, key+1);
push(&st, right);
}//右区间找key
}
destroy(&st);//记得销毁栈
}
这里要想先出右区间也可以,左右区间顺序不影响,两个 if 语句可以互换,所以遇到题可以非递归和递归实现的,我们尽量非递归优先。
归并排序
好看的玫瑰扎手手,高效的排序也不简单

归并归并,也就是合并出一个有序序列,也是采用递归+分治思想的典型。
他的原理就是左右区间有序情况下,直接借助第三方数组进行合并;但一般不会有序,比如我手上有一个 8 个数字的无序序列,我们需要把 8 掰成 4,4 掰成 2,2 掰成 1,1个1个的比,比完就原路归并回去,这里的分割要靠递归实现。
我们就先给分割单独写个函数出来:
void Mergeson(int* a, int head, int tail, int* tem)
{
if (a == NULL)
{
return NULL;
}
if (head >= tail)
{
return;
}
int mid = (tail + head) / 2;//算出两两元素的 mid 值
Mergeson(a, head, mid, tem);//左区间【head,mid】
Mergeson(a, mid + 1, tail, tem);//右区间【mid+1,tail】
}
为什么不把【head,tail】分成【head,mid-1】和【mid,tail】,而是【head,mid】和【mid+1,tail】呢?因为前者分割方式可能出现死循环,比如随便代入一个【1,2】会被分成【1,0】【1,2】就这么死循环了。
接下来就是归并的实现,递归是最终分到 1 个,一一归并,然后二二归并,然后四四归并……


void Mergeson(int* a, int head, int tail, int* tem)
{
if (a == NULL)
{
return NULL;
}
if (head >= tail)
{
return;
}
int mid = (tail + head) / 2;
Mergeson(a, head, mid, tem);
Mergeson(a, mid + 1, tail, tem);
int left = head;
int right = mid;
int left2 = mid + 1;
int right2 = tail;
int count = head;
while (left <= right && left2 <= right2)//区间大小比较
{
if (a[left] < a[left2])
{
tem[count++] = a[left++];//序列每次选出最小单位放入第三方数组
}
else
{
tem[count++] = a[left2++];
}
}
while (left <= right)
{
tem[count++] = a[left++];
}
while (left2 <= right2)
{
tem[count++] = a[left2++];
}
memcpy(a + head, (tail - head + 1) * sizeof(int));//数据拷贝回原数组,加上 head 每次更新位置
}
void Merge(int* a, int n)
{
int* tem = (int*)malloc(sizeof(int) * n);
assert(tem);
Mergeson(a, 0, n - 1, tem);//子序列归并
free(tem);
}
非递归归并
我们非递归就可以不要递归帮我们分,我们自己分不也香香吗?我们需要一个变量来控制跨度,思路和希尔排序的 gap 模型有异曲同工之妙,我们控制 gap 为 1,2,4,8……,直到 gap >= 个数就停下啦。

这过程看似简单,但是后面控制边界能把你心态搞炸,稍不注意就会崩,再次疯狂对递归思想进行夸夸(埋个伏笔,建议忽略)

void MergeNopass(int* a, int n)
{
int* tem = (int*)malloc(sizeof(int) * n);
int gap = 1;//间距为 gap 两两一组归并
for (int i = 0;i<n;i+=2*gap)
{
int left = i;
int right = i+gap-1;
int left2 = i+gap;
int right2 = i+2*gap-1;
int count = i;
while (left <= right && left2 <= right2)
{
if (a[left] < a[left2])
{
tem[count++] = a[left++];
}
else
{
tem[count++] = a[left2++];
}
}
while (left <= right)
{
tem[count++] = a[left++];
}
while (left2 <= right2)
{
tem[count++] = a[left2++];
}
memcpy(a, tem, n * sizeof(int));
}
free(tem);
}
但是程序到这里是有问题的,我们会存在边界问题。比如我们搞一个大小为 6 的数组,问题就比较明显了,我们用
printf("归并对象为【%d,%d】【%d,%d】\n", left, right, left2, right2);
就能很好的看出每次归并对象的下标

很明显这里的 [6,7],[4,7] 都发生了越界问题,我们就需要考虑越界对象,其实 left 是不会越界的,但 right,left2,right2 都有发生越界的可能,我们就要考虑三种情况:
void MergeNopass(int* a, int n)
{
int* tem = (int*)malloc(sizeof(int) * n);
int gap = 1;
int left = 0;
int right = 0;
int left2 = 0;
int right2 = 0;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
left = i;
right = i + gap - 1;
left2 = i + gap;
right2 = i + 2 * gap - 1;
if (right > n)//判断right越界
{
right = n - 1;
}
if (left2 >= n)//left2越界,第二个区间不存在
{
left2 = n;
right2 = n - 1;//没必要归并,直接修正成一个不存在的区间
}
if (right2 >= n)//right2越界
{
right2 = n - 1;
}
int count = i;
while (left <= right && left2 <= right2)
{
if (a[left] < a[left2])
{
tem[count++] = a[left++];
}
else
{
tem[count++] = a[left2++];
}
}
while (left <= right)
{
tem[count++] = a[left++];
}
while (left2 <= right2)
{
tem[count++] = a[left2++];
}
memcpy(a, tem, n * sizeof(int));
gap *= 2;
}
}
free(tem);
}//归并非递归




