不同压强下ZnO的声子谱计算及其收敛性测试

通常对于一个经费不是那么充足，即没什么经费的计算模拟课题组来说（我没说我组，没说），究竟整几台服务器是个大问题。服务器的使用又经常会出现以组会为周期特征，以审稿意见为诱发因子的使用高峰期，和相应的低峰期，难以互补。故而超算就可以作为很好的润滑剂来使用。

北鲲云能够基本满足一切我等对超算的幻想，对于导师来说，最重要的肯定是便宜，便宜，和便宜；对于学生来说，最重要的则是简单，简单，傻瓜式的简单。前者我们可以在后续的计算中管窥一斑，后者，大家点开北鲲云的主页注册一下，登录控制台看一看就知道了。大部分常用的科研软件均皆预装，点开即用；所有过程都是点一点、拖一拖，无脑式完成。并且注册所赠送的试用金，真的够计算出不少东西的。这个刷新了我对超算所存有过的偏见。

在本文中，我来做一系列简单的声子谱和分析，来为大家演示在宝藏云中一站式科研的全过程。对于材料模拟来说，确定它的动力学稳定性是非常关键的一点。声子谱G点下的小小虚频，也是无数人的噩梦。但实际上即便是计算“出错”的声子谱，也是包含很多信息的，这一点我还尚在学习，将一点心得与此计算过程一切记录下来。我们来计算三维体材料ZnO在常压下和19Gpa静水压下的声子谱，每一个声子谱计算对他进行k点的测试，最后我们将声子谱对不同原子进行投影，进一步分析他的晶格振动情况。

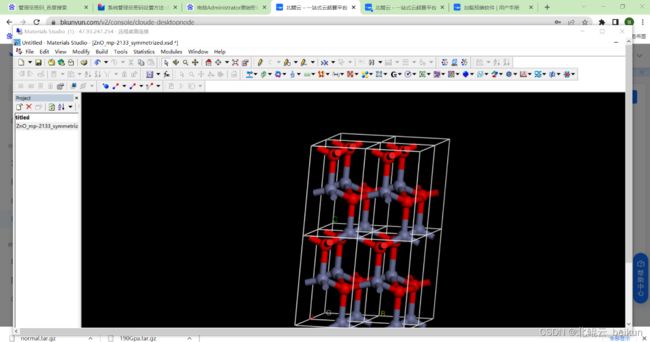
相当的酷炫，也很流畅，对于我来说，MS只用来建模，所以装一个几个G的东西，很划不来，调用一个4核节点，一小时3毛2。

1，

a) 常压优化INCAR 与 晶格常数

晶格常数：3.165（a、b），5.106（c）

b) 190Gpa INCAR 与 晶格常数。

晶格常数：3.165（a、b），5.106（c）

我专门上vasp论坛看过，静水压的单位KB = 0.1Gpa。

2， 平平无奇的声子谱计算：

对两种晶格，按网传的10埃米原理，进行3-4-2的扩胞，共96个原子。对得到的超胞在1x1x1,2x2x2,3x3x3点网格下进行声子谱计算，以查看其收敛情况。声子谱输入文件如下：

在进行1x1x1（即单G点）计算时，我们可以采取单G点版本来计算，以缩短计算时间。只要简单的把提交任务脚本中的vasp_std 修改为 vasp_gam。(记得在计算更大k点的时候要调回来)，另外涂抹方案如-5，是不支持低k点计算的。

真正开展计算的时候，这96原子的单点计算，我调用了一个64核的节点，竟然20分钟左右就算完了，虽然体材料的计算确实相对耗时短，还是被吓了一跳，我刚出门接了热水冲了速溶咖啡准备嗦一会儿，打开看看算到哪儿了，是个什么运算速度。嗯？算……算完了？不对啊，这不应该是提交任务之后的刷剧时间吗，怎么算完了？全部的六个算完抛去失误算错的部分只在百元附近。

3， 投影声子谱

a）在计算所得的声子谱目录下，调用phonphy，提取力常数

phonopy --fc vasprun.xml

b）再编写bond.conf文件，并键入命令，获得band.yaml文件

文件

ATOM_NAME =Zn O

DIM = 3 4 2

NPOINTS = 301

BAND = 0.000000 0.000000 0.000000 0.000000 0.000000 0.500000 0.333333 0.3333333 0.000000 0.000000 0.000000 0.000000

FORCE_CONSTANTS = READ

EIGENVECTORS = .TRUE.

BAND_POINTS = 301

命令：

phonopy --dim=“3 4 2” -c POSCAR-unitcell -p band.conf

c）此时，我们调用后处理神器vaspkit1.12，调用73-739,得到声子谱在各原子中的权重。

d）这时，我们暂时先不管权重，绘制普通的声子谱。

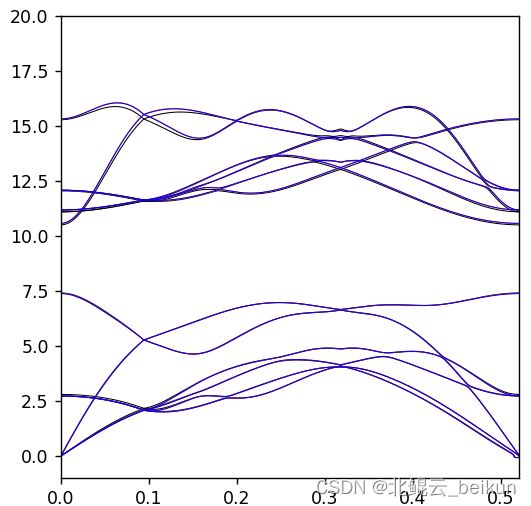
左上左下 常压和19Gpa的声子谱，右上右下局域放大。

可以看到三个k点所计算出的声子谱基本叠在一起，不放大几乎不能分辨，说明此时的收敛程度还是不错的。在19Gpa压强下，声子谱的样式并无太大变化，而是整体“升高”了许多，说明此时他还是稳定的，某学报上刊登的文章计算出19Gpa下有围绕在g点附近的小虚频，我任务可能是收敛问题，或者是泛函问题。这里的结果也说明，大多数情况下单G点的计算结果就能说明很多问题，所以我经常先用单g点声子谱计算粗略的试探其稳定性。

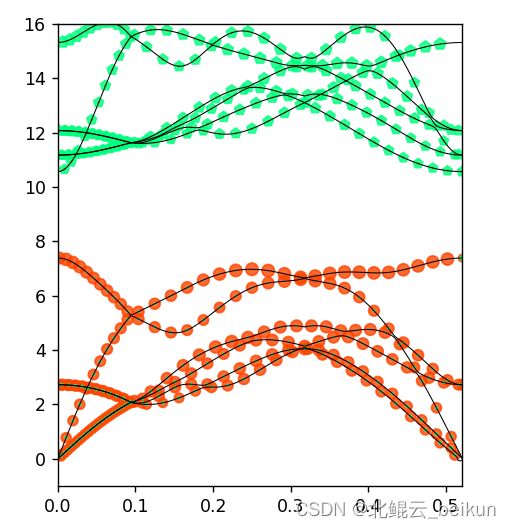
e）我们进一步绘制投影声子谱来分析不同原子的贡献，我们用vaspkit提取出来的数据有

就是按POSCAR顺序排布的，Zn,Zn,O,O的投影情况。每个文件前两列为声子谱图像，后面为权重。此时我们只要选取一个Zn和O原子的文件，即1，3来画投影图即可。可将数据导入origin利用其权重气泡图功能，手搓半天绘制此图。但是，经常面对大量材料的我们，手搓浪费生命，现在像大家介绍我针对vaspkit后处理结果所写的外行看了嘬牙，新手看了叹气，老鸟看了脑淤血的后后处理python制图脚本（上述普通声子谱也是用这个脚本画的，只要去掉散点图部分，重复两遍平平无奇部分）

此外，当我们面对虚频时，我们还可以利用jmol查看虚频振动模式，甚至去提取他的虚频振动本征矢，来确定虚频产生的振动方向，做一个微小的位移来进行能量曲线拟合，找到能量最小值的稳定结果，称为“冻声子法”。

（脚本在附件中）

#河北工业大学北辰校区木华园东六A203宿舍进门靠窗左手那个铺理论物理研究所

#*********************************************************************

#全自动哪儿都可调投影声子谱产生器2.0**************

#*********************************************************************

#注意该产生器不能直接在linux上用，因为他有中文，哈哈。

#加个参数就行了，但是懒得找了。

import matplotlib.pyplot as plt

from numpy import *

import numpy as np

import pandas as pd

import os

import fileinput

#前置可爱小函数

def reline(filename,keywords,mystr):

with open(filename, “r”, encoding=“utf-8”) as f:

lines = f.readlines()

with open(filename, “w”, encoding=“utf-8”) as f_w:

for line in lines:

if keywords in line:

line = line.replace(line, mystr)

f_w.write(line)

def reword(filename,keywords,mystr):

with open(filename, “r”, encoding=“utf-8”) as f:

lines = f.readlines()

with open(filename, “w”, encoding=“utf-8”) as f_w:

for line in lines:

if keywords in line:

line = line.replace(keywords, mystr)

f_w.write(line)

def extractdata(filename):

reline(filename,‘#’,’ ong ma ni bei mei hong’+‘\n’)

reword(filename,’ ‘,’ ')

reword(filename,’ ‘,’ ')

data=pd.read_csv(filename,sep=’ ')

return data

#读取数据,注意备份，因为是直接在原文件上处理的

data1 = extractdata(‘partial_atom_1.dat’)

data3 = extractdata(‘partial_atom_3.dat’)

global ReductNumber

global MeanNumber

ReductNumber = 0

MeanNumber = 0

pnumberlist= range(380,400,1)#输入一个数值区间，在此区间寻找能被数据数整除的数，作为撒点数

X1 = list(data1.iloc[:,1])

Y1 = list(data1.iloc[:,2])

TotalNumber = len(X1)

#背景板声子谱平平无奇直线图

nnum = -1

hnum = 0

for i in X1:

nnum = nnum + 1

if i == X1[0]:

hnum = hnum + 1

print(“found it”)

if hnum == 2:

break

LineNumber = int(TotalNumber / nnum)

print(LineNumber)

for i in range(1,LineNumber+1,1):

sta = (i-1)*nnum

end = i*nnum-1

X = list(data1.iloc[sta:end,1])

Y = list(data1.iloc[sta:end,2])

plt.plot(X,Y,color=‘black’,linewidth=0.6)

#约化撒点点数

for i in pnumberlist:

Yu = TotalNumber % i

if Yu == 0:

ReductNumber = int(i)

MeanNumber =int(TotalNumber/i)

print(“约化点数为”+str(i)+“,开始取均值”)

break

else:

print(str(i)+“不能被整除”)

if ReductNumber == 0:

print(“区间不合理”)

#求取撒点区间内平均值，输出约化过的x,y坐标和权重值

def MeanTheValue(RN,MN,data):

RX = list()

RY = list()

Rs = list()

for i in range(1,RN,1):

num = int(i-1)

sta = int(MN*num)

end = int(MN*i-1)

median = int((end+sta)/2)

X = list(data.iloc[:,1])

Y = list(data.iloc[:,2])

RX.append(X[median])

RY.append(Y[median])

Rs.append(mean(list(data.iloc[sta:end,6])))

S = np.array(Rs)

RS = list((2.5np.pi(S*5)**2)) #权重面积函数

return RX,RY,RS

RX1,RY1,RS1 = MeanTheValue(ReductNumber,MeanNumber,data1)

RX2,RY2,RS2 = MeanTheValue(ReductNumber,MeanNumber,data3)

#画约化权重散点图

plt.xlim([0,X1[nnum-1]])

plt.ylim([-1,16])

plt.scatter(RX1,RY1,s=RS1,c=‘orangered’,alpha=0.8)

plt.scatter(RX2,RY2,s=RS2,c=‘springgreen’,alpha=0.8,marker=‘p’)

plt.gca().set_aspect(0.035, adjustable=‘box’)

plt.show()