（无监督）Python实现PCA算法（数据特征降维）(学习笔记)

一、前言

PCA算法算是一个比较简单的无监督机器学习算法。主要作用就是用作数据样本特征降维。个人对于PCA算法的理解是通过变换坐标系，从而将高维度样本压缩到低维度，同时还尽可能的保留样本数据的大部分信息。
PCA算法在实际项目应用中的作用包括以下几个方面：

• 用在数据预处理方面，在监督学习算法中，输入样本维度非常大的时候，此时为了加速学习算法可以利用pca算法降低样本维度，减小内存，提高运行效率。
• 当高维样本不容易可视化的时候，可以将样本进行压缩到2,3维度，从而方便数据的可视化。
• 多维样本压缩之后的变量命名，找到主要影响因素指标
• pca算法不是数据必须的，当计算机运行时间不是很长时候尽量还是使用原始样本作为输入。

FLAG：以后相关的机器学习算法都要自己编程实现，然后和相关的库函数实现做一个对比。

二、实验环境

• python3.6.4
• IDE：Pycharm 2018
• 操作系统：windows10
• 吴恩达课程作业数据
• 噪声单车源强
• 依赖库：scipy，matplotlib， numpy，pandas，sklearn

三、PCA的基本原理

---

3.1、算法简介

在多元统计分析中，主成分分析（英语：Principal components analysis，PCA）是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分（Principal Components）。具体地，主成分可以看做一个线性方程，其包含一系列线性系数来指示投影方向。PCA对原始数据的正则化或预处理敏感（相对缩放）。

3.2、PCA的数学推导

对于PCA的推导过程，我们在这里简要的介绍推导的思想，详细步骤给出相关链接。

我们的初始矩阵为X，它是m×n维的矩阵，矩阵X每一行就是一条记录，每一列就是特征，我们想要对它降维，也就是想让它从m×n维降到m×r维(n>r)。可以通过乘以一个满秩矩阵映射到其他坐标系让它特征变少。
设变换矩阵为P，P为n×r的满秩矩阵，原始数据集X经过P变换，成为Y(m×r维)，即：Y=X•P，我们知道右乘一个满秩矩阵来进行坐标变换，其实就是数据向这些新的基向量上投影，而这个满秩矩阵P就是新的基向量组成的矩阵。我们的目标就是找到这样的基向量，也就是矩阵P。

可以从从两个角度进行推导：

• 要求这变换后的矩阵Y，让它损失的信息最少，因为Y比原始矩阵X维数低，肯定在变换的过程中损失了一些信息，现在我们要求损失的信息最少。我们描述分散程度用方差来表示，在变换后的数据集矩阵Y(m×r维)中，一个字段的方差可以看做是每个元素与字段均值的差的平方和的均值。从而可以推导出Y的协方差矩阵。
• 第二个就是要求变换后的Y矩阵每一列(一列就是一个字段)之间都是不相关的，在数学中，描述变量之间的相关性可用协方差来描述，只要让协方差为0。最终同样是推导出Y的协方差矩阵。

Y的协方差矩阵，要正好满足上述两个要求。从而进一步推导出X的协方差矩阵，通过特征值分解来找出选取特征值对应的特征向量作为基向量，组成p矩阵。比如我们要降维到m×r维，只需取\Lambda中前r个特征值，然后从Q中找到这r个特征值对应的特征向量[ Q1,Q2,…Qr ]，这些特征向量组成的矩阵就是我们要找的P矩阵。

对于严格的数学推倒过程，这里就不在讲解，具体可以参考以下文章：

• python实现PCA
• 主成分分析–维基百科

---

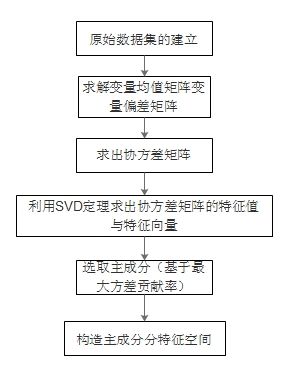
3.3、算法迭代步骤

• step1：数据预处理，样本中心化（特征归一化）；
• step2：求出均值化X的协方差矩阵；
• step3：求这个协方差矩阵的特征值，特征向量，（特征值分解，SVD定理）
• step4：选取主成分特征值以及对应的特征向量构造主元子空间
• step5：计算X映射到“特征空间”从而得到特征变量。

算法流程图如下：

---

四、PCA算法的编程实现（python）

本实例的测试样本数据包括了：

• 吴恩达课程作业数据
• 噪声单车源强

PCA算法实现的脚本如下：

#!/usr/bin/env python 
# -*- coding:utf-8 -*-
import scipy.io as sio # load mat
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn import decomposition

# 这两句代码用来正确显示图中的中文字体，后续都要加上
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

#读入吴恩达课后习题数据作为实验样本
data = sio.loadmat(r'C:\Users\13109\Desktop\机器学习\machine-learning-ex7\ex7\ex7data1.mat')
X = data['X']

#读入大车噪声的单车源强数据作为实验样本（样本4个维度分别是声压级1，声压级2，大车测速，雷达测速）
df = pd.read_excel('C:/Users/13109/desktop/单车源强数据2.xlsx','大车',na_vlues=['NA'])
df = df.iloc[:,2:6]
df = df.dropna(how='any')#删除任何带有空值的行
df= df.values
# print(df)
#可视化原始数据集
plt.plot(X[:,0],X[:,1],'o',color ='#ff8c31')
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('吴恩达课后习题原数据')
plt.show()
#数据预处理，样本中心化(样本归一化)
def feature_normalize(X):
    mean = np.mean(X,axis=0)#按列取均值
    sj = np.std(X,axis=0)#列取方差
    X_norm = (X-mean)/sj#归一化，中心化
    return X_norm,mean,sj

data,mean,sj = feature_normalize(X)

#PCA算法的实现
def pca(data,k):
    m,n = data.shape
    sigma = np.cov(data,rowvar=0)
    #其中U是特征向量，S为特征值
    U,S,V= np.linalg.svd(sigma)#特征值分解U, S = np.linalg.eig(sigma)
    gongxin = np.sum(S[0:k])/np.sum(S)#计算累计方差贡献率
    u_reduce = U[:, :k]#抽出主成分特征向量(k表示抽取维度，也就是降低到K维)
    z = data.dot(u_reduce)#归一化数据向主成分特征向量投影得到降维结果
    x_rec = z.dot(u_reduce.T)*sj+mean#维度还原之后的映射
    return U,S,gongxin,z,x_rec

U,S,gongxin,z,x_rec = pca(data,1)
# print(U)#打印特征向量
# print(S)#打印特征值
# print(gongxin)#打印方差贡献率
# print(z)#打印降维之后的变量
# print(x_rec)#打印维度还原之后的数据

#二维样本降维到一维样本可以可视化
plt.plot(X[:,0],X[:,1],'bo',label='原数据')
plt.plot(x_rec[:,0],x_rec[:,1],'*',color ='#ff8c31',label='降维还原数据点')
# plt.plot(z[:,0],z[:,1],'rx')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend()
plt.title('吴恩达课程作业PCA可视化')
plt.show()

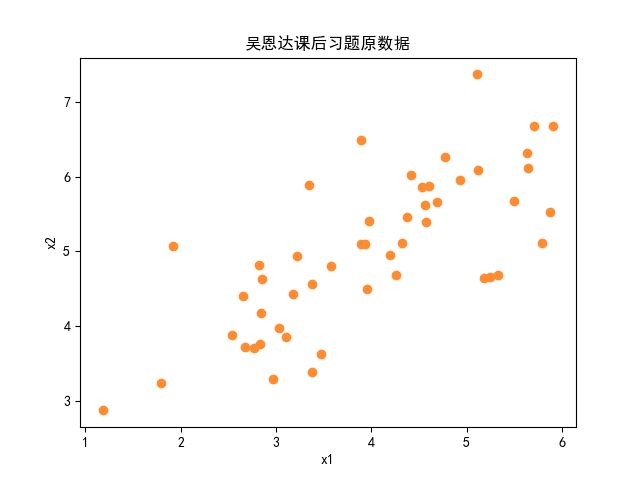
• 脚本输出结果图，首先是原始样本的散点图：

• 吴恩达课程作业，二维样本降维还原结果

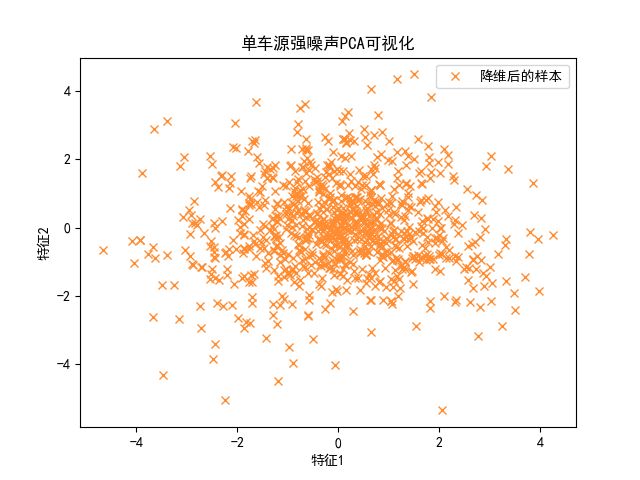
通过修改一些参数，将上述样本应用在单车源强大车数据上面，大车噪声的单车源强数据实验样本（样本4个维度分别是声压级1，声压级2，大车测速，雷达测速）。最终可以得到单车源强数据从四维压缩到二维，仍然保留原始数据的98.3%的信息。（累计方差贡献率达到了98.3%）

• 单车源强噪声，四维样本降维还原结果的可视化

上面的代码是自己编程实现的pca算法，下面我们再来直接调用scikit-learn库相关的代码来实现pca，使用的数据还是那两个。

五、PCA算法的scikit-learn库实现

实现的脚本如下

'''
用Python的sklearn库进行PCA（主成分分析）

sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)  
对象属性：
components_：返回具有最大方差的成分。 
explained_variance_ratio_：返回 所保留的n个成分各自的方差百分比。 
n_components_：返回所保留的成分个数n。
fit(X,y=None) 
fit()可以说是scikit-learn中通用的方法，每个需要训练的算法都会有fit()方法，它其实就是算法中的“训练”这一步骤。因为PCA是无监督学习算法，此处y自然等于None。 
fit(X)，表示用数据X来训练PCA模型。函数返回值：调用fit方法的对象本身。比如pca.fit(X)，表示用X对pca这个对象进行训练。 
fit_transform(X) 
用X来训练PCA模型，同时返回降维后的数据。 
newX=pca.fit_transform(X)，newX就是降维后的数据。 
inverse_transform() 
将降维后的数据转换成原始数据，X=pca.inverse_transform(newX) 
transform(X) 
将数据X转换成降维后的数据。当模型训练好后，对于新输入的数据，都可以用transform方法来降维。

'''

###首先测试吴恩达课程作业的样本数据
pca = decomposition.PCA(n_components=1)
pca.fit(X)
print(pca.explained_variance_ratio_)#打印方差贡献率
print(gongxin)#自己写的脚本输出方差贡献率
# print(pca.explained_variance_)#打印方差

#将降维后的数据返回(一维)
x_pca = pca.transform(X)#返回降维之后的数据
X1 = pca.inverse_transform(x_pca)#降维后的数据转换成原始维度
# print(x_pca)
plt.plot(X[:,0],X[:,1],'o',color ='#ff8c31')
plt.scatter(X1[:, 0], X1[:, 1],marker='o')
plt.show()


###测试自己的噪声数据样本降维情况

#绘制碎石图确定维度
def nd_confirm(data,n):
    std = []
    for i in range(1,n):
        pca = decomposition.PCA(n_components=i)
        pca.fit(data)
        std.append(np.sum(pca.explained_variance_ratio_))
    # return std
    x = range(1,n)
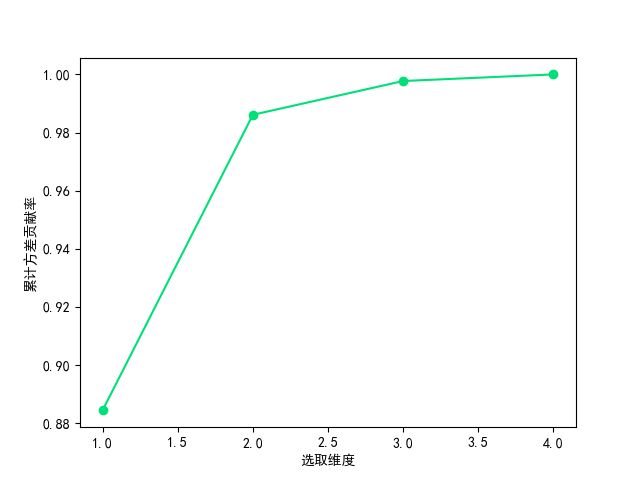
    plt.plot(x,std,'-o',color='#00e079')
    plt.xlabel('选取维度')
    plt.ylabel('累计方差贡献率')
    plt.show()
nd_confirm(df,5)

###根据上面的碎石图，我们可以确定出最好维度应该是2

pca = decomposition.PCA(n_components=2)
pca.fit(df)
print(np.sum(pca.explained_variance_ratio_))#打印方差贡献率
print(gongxin)#自己写的脚本输出方差贡献率
# print(pca.explained_variance_)#打印方差

#将降维后的数据返回(一维)
x_pca = pca.transform(df)#返回降维之后的数据
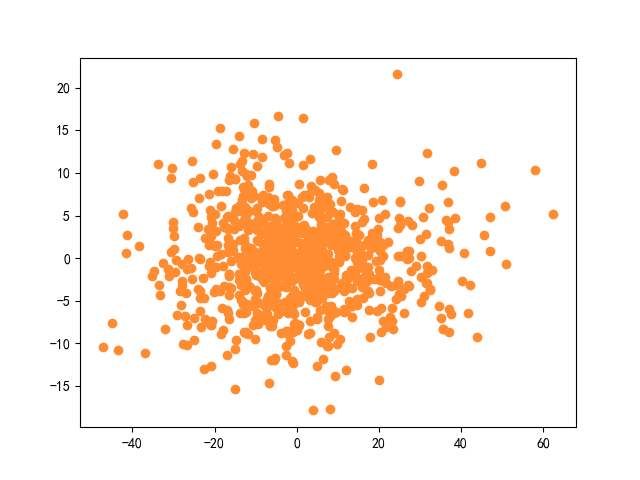
plt.plot(x_pca[:,0],x_pca[:,1],'o',color ='#ff8c31')
plt.show()

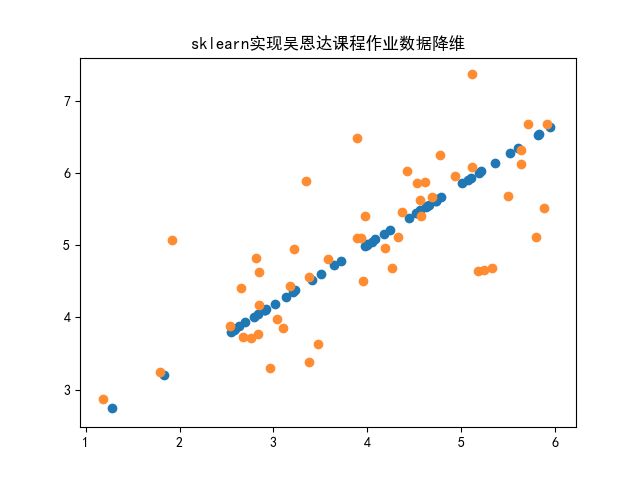
• 使用scikit-learnj机器学习库实现吴恩达课程作业数据的迭代结果图如下：

• 使用scikit-learnj机器学习库实现噪声数据降维的结果：

绘制降维碎石图：

根据上述的碎石图可以确定降维的维度为2维，可以得到降维样本的可视化如下：

• 实验对比(自编脚本和scikit-learnj机器学习库实现的对比)
  对于PCA算法，我们主要对比的指标是累计方差贡献率。这里对比的是4维噪声数据的降维情况

(machine_learning) D:\CloudMusic\virtualenv\machine_learning\machine>python PCA.py
0.9860990796045223
0.9826663983425054

根据上述的累计方差贡献率对比可以看出，两者差距不大，微小的差异有可能是由于数据预处理部分，对于数据的中心化处理，我对数据又进行了伸缩处理，中心化之后又除以了一个样本的方差。

六、总结

PCA算法的主要优点：

• 1、仅仅需要以方差衡量信息量，不受数据集以外的因素影响。
• 2、各主成分之间正交，可消除原始数据成分间的相互影响的因素。
• 3、降维的过程中有可能直接消除噪声，保留主要信息
• 4、计算方法简单，主要运算是特征值分解，易于实现。

PCA算法的主要缺点：

• 1、主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
• 2、方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点，出现了很多PCA的变种，比如为解决非线性降维的KPCA，还有解决内存限制的增量PCA方法Incremental PCA，以及解决稀疏数据降维的PCA方法Sparse PCA等。这些变种算法，在实际应用到的时候还会再写文章记录。

七、参考文章链接和推荐的教程

• 吴恩达机器学习-降维-PCA
• 【机器学习】Sklearn库主成分分析PCA降维的运用实战
• python实现PCA
• pandas库的基础入门
• python之sklearn学习笔记
• NumPy 中文文档