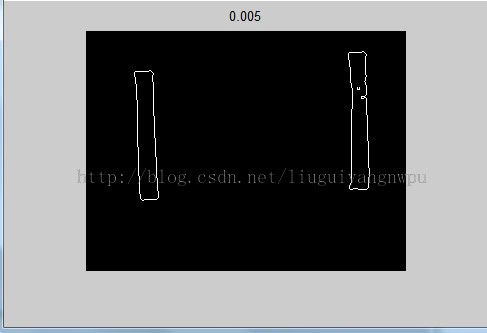
自动阈值分割-场景中直线个数的检测
问题:
在竞速机器人的比赛中,我们使用计算机视觉导航进行跑道路线的识别
目标:
在不同的情况下可以得到采集到的图片中直线的个数,以及直线的斜率,进而判断机器人的具体位置
不同的环境,包括:晴天,阴天,室内,室外,阴影区,和非阴影区,摄像头的曝光区,和非曝光区
具体图片:

该图像包含阴影区和反光区
先进行RGB到灰度图的转换
clear all;
close all;
clc
img = imread('1.jpg');
img = imresize(img,[240,320]);
%%
%先进行颜色空间的转换
[row col dim] = size(img);
T = zeros([row ,col]);
A = [0.299 0.587 0.114];
for i=1:row
for j=1:col
B = [img(i,j,1) img(i,j,2) img(i,j,3)]';
T(i,j) = A*double(B);
end
end
new_img = uint8(T);
figure ;imshow(new_img);title('自己转换的图片');
紧接着进行阈值分割点的查找
%%
%进行阈值分割
Grade_Level = zeros(1,256);
for x = 1:row
for y = 1:col
Grade_Level(new_img(x,y)+1) = Grade_Level(new_img(x,y)+1) + 1;
end
end
figure;plot(1:256,Grade_Level);title('灰度直方图');
%%
%寻找分割点
num_bins=256;
counts = Grade_Level(:);
p = counts / sum(counts);
omega = cumsum(p);
mu = cumsum(p .* (1:num_bins)');
mu_t = mu(end);
sigma_b_squared = (mu_t * omega - mu).^2 ./ (omega .* (1 - omega));
% Find the location of the maximum value of sigma_b_squared.
% The maximum may extend over several bins, so average together the
% locations. If maxval is NaN, meaning that sigma_b_squared is all NaN,
% then return 0.
maxval = max(sigma_b_squared);
isfinite_maxval = isfinite(maxval);
if isfinite_maxval
idx = mean(find(sigma_b_squared == maxval));
pos_threshold = (idx - 1) / (num_bins - 1);
else
pos_threshold = 0.0;
end
pos_threshold = pos_threshold*(num_bins-1);
%%
pos_index = 1;
for i=1:row
for j=1:col
if new_img(i,j) > pos_threshold
new_img(i,j) = 255;
else
new_img(i,j) = 0;
Img_posX(pos_index) = i;
Img_posY(pos_index) = j;
pos_index = pos_index + 1;
end
end
end
figure ; imshow(new_img);


然后检测图片中的直线的条数
%%
%进行直线的分割
%利用扫描线算法确定直线的条数
%主要思路:找到一个点,然后直接在周围寻找点
%该点的四邻域内的点如果都是黑色的就把该点放进去
Point.x = -1;
Point.y = -1;
first_line(1) = Point;
iterator = 0;
max_Target_line = 0;
line_Cell = cell(3,1);
for i=2:row-1
curRow = i;%表明现在做的任何处理都是针对当前行的处理
num_line = 0;%一行扫描下来得到的目标线的个数
isChanged = 0;%表示没有改变
temp_flag = -1;
for j=2:col-1
num = new_img(i,j);
if num == 255 && (num == new_img(i,j-1)...
&& num == new_img(i,j+1)...
&& num == new_img(i-1,j)...
&& num == new_img(i+1,j))
if isChanged == 1
temp_flag = temp_flag * -1;
isChanged = 0;
num_line = num_line + 1;
%发现了一条直线,然后记录下直线的位置,作为该直线的大体位置
end
end
%当前的点为目标点,且直线的四邻域的值也都为目标点
if num == 0 && (num == new_img(i,j-1)...
&& num == new_img(i,j+1)...
&& num == new_img(i-1,j)...
&& num == new_img(i+1,j))
if isChanged == 0
isChanged = 1;
end
iterator = iterator + 1;
Point.x = i;
Point.y = j;
first_line(iterator) = Point;
end
end
if num_line > max_Target_line
max_Target_line = num_line;
end
end
max_Target_line
剩下的就是最下二乘法的拟合程序:
%%
%对直线点集进行最小二乘法拟合,求出直线的斜率
sum_x = 0;
sum_y = 0;
sum_mul = 0;
sum_squar = 0;
first_line = line_Cell{1};
N = length(first_line);
for i=1:N
sum_x = sum_x + first_line(i).x;
sum_y = sum_y + first_line(i).y;
sum_mul = sum_mul + first_line(i).x*first_line(i).y;
sum_squar = sum_squar + (first_line(i).x)^2;
end
mean_x = sum_x*1.0/n;
mean_y = sum_y*1.0/n;
sum_Xdelta = 0;
sum_Ydelta = 0;
for i=1:N
sum_Xdelta = sum_Xdelta + (first_line(i).x-mean_x)^2;
sum_Ydelta = sum_Ydelta + (first_line(i).y-mean_y)^2;
end
delta_x = (sum_Xdelta*1.0/n)^0.5;
delta_y = (sum_Ydelta*1.0/n)^0.5;
temp_sum = 0;
for i=1:N
temp_sum = temp_sum + (first_line(i).x-mean_x)*(first_line(i).y-mean_y)/(delta_x*delta_y);
end
disp('直线的相关系数');
relative_line = temp_sum/n
disp('直线的斜率');
betha = (n*sum_mul-sum_x*sum_y)*1.0/(n*sum_squar-sum_x^2)
如果要检测图片中的真正直线的个数,可以采用huogh直线检测的算法来检测
%%
%Hough变换检测直线,使用(a,p)参数空间,a∈[0,180],p∈[0,2d]
a=180; %角度的值为0到180度
d=round(sqrt(m^2+n^2)); %图像对角线长度为p的最大值
s=zeros(a,2*d); %存储每个(a,p)个数
z=cell(a,2*d); %用元胞存储每个被检测的点的坐标
for i=1:m
for j=1:n %遍历图像每个点
if(q(i,j)==1) %只检测图像边缘的白点,其余点不检测
for k=1:a
p = round(i*cos(pi*k/180)+j*sin(pi*k/180)); %对每个点从1到180度遍历一遍,取得经过该点的所有直线的p值(取整)
if(p > 0)%若p大于0,则将点存储在(d,2d)空间
s(k,d+p)=s(k,d+p)+1; %(a,p)相应的累加器单元加一
z{k,d+p}=[z{k,d+p},[i,j]'];%存储点坐标
else%相当于a为0到-180
ap=abs(p)+1;%若p小于0,则将点存储在(0,d)空间
s(k,ap)=s(k,ap)+1;%(a,p)相应的累加器单元加一
z{k,ap}=[z{k,ap},[i,j]'];%存储点坐标
end
end
end
end
end
angle_num=1;
for i=1:a
for j=1:d*2 %检查每个累加器单元中存储数量
if(s(i,j) >55) %将提取直线的阈值设为70
angle(angle_num)=i;
angle_num=angle_num+1;
lp=z{i,j};%提取对应点坐标
for k=1:s(i,j)%对满足阈值条件的累加器单元中(a,p)对应的所有点进行操作
o(lp(1,k),lp(2,k),1)=255; %每个点R分量=255,G分量=0,B分量=0
o(lp(1,k),lp(2,k),2)=0;
o(lp(1,k),lp(2,k),3)=0; %结果为在原图上对满足阈值要求的直线上的点赋红色
end
end
end
end
figure,imshow(o);title('hough变换提取直线');