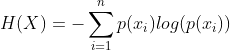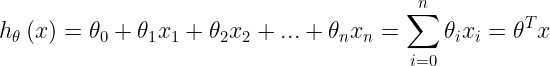活胶力

机器学习从零到一的基础知识总集篇

机器学习是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。

文章目录

- 1. 定义
- 2. 机器学习原理
- 3. 机器学习的分类
- - 3.1 基于学习策略的分类
  - 3.2 基于学习方法的分类
  - 3.3 基于学习方式的分类
  - 3.4 基于数据形式的分类
  - 3.5 基于学习目标的分类
- 4. 常见算法
- - 4.1 决策树算法
  - 4.2 朴素贝叶斯算法
  - 4.3 支持向量机算法
  - 4.4 随机森林算法
  - 4.5 人工神经网络算法
  - 4.6 Boosting与Bagging算法
  - 4.7 关联规则算法
  - 4.8 EM（期望最大化）算法
  - 4.9 深度学习
- 5. 应用
- - 5.1 数据分析与挖掘
  - 5.2 模式识别
  - 5.3 在生物信息学上的应用
  - 5.4 更广阔的领域
  - 5.5 具体应用
- 6. 数据学习开发流程
- 7. 学习目标
- 8. 数据集
- - 8.1 数据集
  - - 8.1.1 可用数据集
- 9. Python数据分析工具介绍
- - 9.1 Scikit-learn工具介绍
  - 9.3 Scikit-learn数据集api介绍
  - 9.4 数据集的划分
- 10.特征工程
- - 10.1 定义
  - 10.2 模块流程
  - - 10.2.1 特征抽取
    - - 10.2.1.1字典特征提取
      - 10.2.1.1文本特征提取
    - 10.2.2 特征预处理
    - - 10.2.2.1.归一化（方法不止这一种）
      - 10.2.2.1.标准化
    - 10.2.3 特征降维
    - - 10.2.3.1 特征选择
      - 10.2.3.2 主成分分析（PCA）
- 案例分析
- - 1. insta_cart市场篮子分析
- 11. 分类算法
- - 11.1 sklearn的转换器和预估器
  - - 11.1.1转换器
    - 11.1.2预估器
  - 11.2 KNN算法
  - - 11.2.1 什么是KNN算法
    - 11.2.2 KNN算法API
    - 11.2.3 案例：莺尾花种类预测
    - 11.2.4 KNN算法总结
    - 优点：KNN方法思路简单，易于理解，易于实现，无需估计参数
  - 11.3 模型选择与调优
  - - 11.3.1 什么是交叉验证
    - 11.3.2 超参数搜索-网格搜索
    - 11.3.3 鸢尾花案例加k值调优
    - 11.3.4 预测fecebook签到
    - 11.3.5 总结
  - 11.4 朴素贝叶斯算法
  - - 11.4.1 定义
    - 11.4.2 概率基础
    - 11.4.3 联合概率、条件概率、与相互独立
    - 11.4.4 贝叶斯公式
    - 11.4.6 案例：20类新闻分类
    - 11.4.7 朴素贝叶斯算法总结
    - 11.4.8 总结
  - 11.5 决策树
  - - 11.5.1认识决策树
    - 11.5.2 决策树分类原理
    - 11.5.3 决策树API
    - 11.5.4 案例:泰坦尼克号乘客生存预测
    - - 11.5.4.1 案例鸢尾花
      - 11.5.4.2 案例泰坦尼克号
    - 11.5.5 决策树可视化
    - 11.5.6 决策树总结
    - 11.5.7 总结
  - 11.6 随机森林
  - - 11.6.1 什么是集成学习方法
    - 11.6.2 什么是随机森林
    - 11.6.3 随机森林原理过程
    - 11.6.4 API
    - 11.6.5 随机森林预测案例
    - 11.6.6 总结
- 12.回归与聚类算法
- - 12.1 线性回归
  - - 12.1.1 线性回归原理
    - - 12.1.1.1 应用场景
      - 12.1.1.2 定义
      - 12.1.1.3 线性回归的特征与目标的关系分析
    - 12.1.2 线性回归的损失与优化原理
    - 12.1.3 方差 - 损失函数 Cost Function
    - 12.1.4 优化方法 Optimization Function
    - - 12.2.2.1 正规方程
      - 12.2.2.2 梯度下降
    - 12.1.5 线性回归API
    - 12.1.6 回归性能评估
    - 12.1.7 波士顿房价预测
  - 12.2 欠拟合与过拟合
  - - 12.2.1 定义
    - 12.2.2 原因及解决方法
    - - 12.2.2.1解决过拟合的方法：
      - 12.2.2.2解决欠拟合的方法：
  - 12.3 线性回归的改进-岭回归
  - - 12.3.1 API
    - 12.3.2 对结果的影响
    - 12.3.3 案例-波士顿房价
  - 12.4 分类算法-逻辑回归与二分类
  - - 12.4.1 逻辑回归的应用场景
    - 12.4.2 逻辑回归的原理
    - 12.4.3 逻辑回顾API
    - 12.4.4 案例癌症分类预算-良/恶性乳腺瘤预测
    - 12.4.5 分类的评估方法
  - 12.5 模型保存与加载
  - 12.6 无监督学习K'聚类
  - - 12.6.1 什么是无监督学习
    - 12.6.2 无监督学习包含算法
    - 12.6.3 K-means原理
    - 12.6.4 k-means API
    - 12.6.5 案例k-means对instacart market用户聚类
    - 12.6.6 K性能评估指标
    - 13.6.7 k聚类总结
  - 13.7 总结
  - - 12.6.4 k-means API
    - 12.6.5 案例k-means对instacart market用户聚类
    - 12.6.6 K性能评估指标
    - 13.6.7 k聚类总结
  - 13.7 总结

1. 定义

定义: （1）机器学习是一门人工智能的科学，该领域的主要研究对象是人工智能，特别是如何在经验学习中改善具体算法的性能。

（2）机器学习是对能通过经验自动改进的计算机算法的研究。

（3）机器学习是用数据或以往的经验，以此优化计算机程序的性能标准。

2. 机器学习原理

原理

3. 机器学习的分类

3.1 基于学习策略的分类

（1）模拟人脑的机器学习

符号学习：模拟人脑的宏现心理级学习过程，以认知心理学原理为基础，以符号数据为输入，以符号运算为方法，用推理过程在图或状态空间中搜索，学习的目标为概念或规则等。符号学习的典型方法有记忆学习、示例学习、演绎学习.类比学习、解释学习等。

神经网络学习（或连接学习）：模拟人脑的微观生理级学习过程，以脑和神经科学原理为基础，以人工神经网络为函数结构模型，以数值数据为输人，以数值运算为方法，用迭代过程在系数向量空间中搜索，学习的目标为函数。典型的连接学习有权值修正学习、拓扑结构学习。

（2）直接采用数学方法的机器学习

主要有统计机器学习。

统计机器学习是基于对数据的初步认识以及学习目的的分析，选择合适的数学模型，拟定超参数，并输入样本数据，依据一定的策略，运用合适的学习算法对模型进行训练，最后运用训练好的模型对数据进行分析预测。

统计机器学习三个要素：

模型（model）：模型在未进行训练前，其可能的参数是多个甚至无穷的，故可能的模型也是多个甚至无穷的，这些模型构成的集合就是假设空间。

策略（strategy）：即从假设空间中挑选出参数最优的模型的准则。模型的分类或预测结果与实际情况的误差（损失函数）越小，模型就越好。那么策略就是误差最小。

算法（algorithm）：即从假设空间中挑选模型的方法（等同于求解最佳的模型参数）。机器学习的参数求解通常都会转化为最优化问题，故学习算法通常是最优化算法，例如最速梯度下降法、牛顿法以及拟牛顿法等。

3.2 基于学习方法的分类

（1）归纳学习

符号归纳学习：典型的符号归纳学习有示例学习、决策树学习。

函数归纳学习（发现学习）：典型的函数归纳学习有神经网络学习、示例学习、发现学习、统计学习。

（2）演绎学习

（3）类比学习：典型的类比学习有案例（范例）学习。

（4）分析学习：典型的分析学习有解释学习、宏操作学习。

3.3 基于学习方式的分类

（1）监督学习（有导师学习）：输入数据中有导师信号，以概率函数、代数函数或人工神经网络为基函数模型，采用迭代计算方法，学习结果为函数。

分类：K近邻、朴素贝叶斯、决策树、SVM。
回归：线性回归、逻辑回归、岭回归。

（2）无监督学习（无导师学习）：输入数据中无导师信号，采用聚类方法，学习结果为类别。典型的无导师学习有发现学习、聚类、竞争学习等。

聚类：K-means

（3）强化学习（增强学习）：以环境反惯（奖/惩信号）作为输入，以统计和动态规划技术为指导的一种学习方法。

半监督学习：深度学习

3.4 基于数据形式的分类

（1）结构化学习：以结构化数据为输入，以数值计算或符号推演为方法。典型的结构化学习有神经网络学习、统计学习、决策树学习、规则学习。

（2）非结构化学习：以非结构化数据为输入，典型的非结构化学习有类比学习案例学习、解释学习、文本挖掘、图像挖掘、Web挖掘等。

3.5 基于学习目标的分类

（1）概念学习：学习的目标和结果为概念，或者说是为了获得概念的学习。典型的概念学习主要有示例学习。

（2）规则学习：学习的目标和结果为规则，或者为了获得规则的学习。典型规则学习主要有决策树学习。

（3）函数学习：学习的目标和结果为函数，或者说是为了获得函数的学习。典型函数学习主要有神经网络学习。

（4）类别学习：学习的目标和结果为对象类，或者说是为了获得类别的学习。典型类别学习主要有聚类分析。

（5）贝叶斯网络学习：学习的目标和结果是贝叶斯网络，或者说是为了获得贝叶斯网络的一种学习。其又可分为结构学习和多数学习。

4. 常见算法

4.1 决策树算法

决策树及其变种是一类将输入空间分成不同的区域，每个区域有独立参数的算法。决策树算法充分利用了树形模型，根节点到一个叶子节点是一条分类的路径规则，每个叶子节点象征一个判断类别。先将样本分成不同的子集，再进行分割递推，直至每个子集得到同类型的样本，从根节点开始测试，到子树再到叶子节点，即可得出预测类别。此方法的特点是结构简单、处理数据效率较高。

4.2 朴素贝叶斯算法

朴素贝叶斯算法是一种分类算法。它不是单一算法，而是一系列算法，它们都有一个共同的原则，即被分类的每个特征都与任何其他特征的值无关。朴素贝叶斯分类器认为这些“特征”中的每一个都独立地贡献概率，而不管特征之间的任何相关性。然而，特征并不总是独立的，这通常被视为朴素贝叶斯算法的缺点。简而言之，朴素贝叶斯算法允许我们使用概率给出一组特征来预测一个类。与其他常见的分类方法相比，朴素贝叶斯算法需要的训练很少。在进行预测之前必须完成的唯一工作是找到特征的个体概率分布的参数，这通常可以快速且确定地完成。这意味着即使对于高维数据点或大量数据点，朴素贝叶斯分类器也可以表现良好。

4.3 支持向量机算法

基本思想可概括如下：首先，要利用一种变换将空间高维化，当然这种变换是非线性的，然后，在新的复杂空间取最优线性分类表面[8]。由此种方式获得的分类函数在形式上类似于神经网络算法。支持向量机是统计学习领域中一个代表性算法，但它与传统方式的思维方法很不同，输入空间、提高维度从而将问题简短化，使问题归结为线性可分的经典解问题。支持向量机应用于垃圾邮件识别，人脸识别等多种分类问题。

4.4 随机森林算法

控制数据树生成的方式有多种，根据前人的经验，大多数时候更倾向选择分裂属性和剪枝，但这并不能解决所有问题，偶尔会遇到噪声或分裂属性过多的问题。基于这种情况，总结每次的结果可以得到袋外数据的估计误差，将它和测试样本的估计误差相结合可以评估组合树学习器的拟合及预测精度。此方法的优点有很多，可以产生高精度的分类器，并能够处理大量的变数，也可以平衡分类资料集之间的误差。

4.5 人工神经网络算法

人工神经网络与神经元组成的异常复杂的网络此大体相似，是个体单元互相连接而成，每个单元有数值量的输入和输出，形式可以为实数或线性组合函数。它先要以一种学习准则去学习，然后才能进行工作。当网络判断错误时，通过学习使其减少犯同样错误的可能性。此方法有很强的泛化能力和非线性映射能力，可以对信息量少的系统进行模型处理。从功能模拟角度看具有并行性，且传递信息速度极快。

4.6 Boosting与Bagging算法

Boosting是种通用的增强基础算法性能的回归分析算法。不需构造一个高精度的回归分析，只需一个粗糙的基础算法即可，再反复调整基础算法就可以得到较好的组合回归模型。它可以将弱学习算法提高为强学习算法，可以应用到其它基础回归算法，如线性回归、神经网络等，来提高精度。Bagging和前一种算法大体相似但又略有差别，主要想法是给出已知的弱学习算法和训练集，它需要经过多轮的计算，才可以得到预测函数列，最后采用投票方式对示例进行判别。

4.7 关联规则算法

关联规则是用规则去描述两个变量或多个变量之间的关系，是客观反映数据本身性质的方法。它是机器学习的一大类任务，可分为两个阶段，先从资料集中找到高频项目组，再去研究它们的关联规则。其得到的分析结果即是对变量间规律的总结。

4.8 EM（期望最大化）算法

在进行机器学习的过程中需要用到极大似然估计等参数估计方法，在有潜在变量的情况下，通常选择EM算法，不是直接对函数对象进行极大估计，而是添加一些数据进行简化计算，再进行极大化模拟。它是对本身受限制或比较难直接处理的数据的极大似然估计算法。

4.9 深度学习

深度学习（DL，Deep Learning）是机器学习（ML，Machine Learning）领域中一个新的研究方向，它被引入机器学习使其更接近于最初的目标——人工智能（AI，Artificial Intelligence）。

深度学习是学习样本数据的内在规律和表示层次，这些学习过程中获得的信息对诸如文字，图像和声音等数据的解释有很大的帮助。它的最终目标是让机器能够像人一样具有分析学习能力，能够识别文字、图像和声音等数据。深度学习是一个复杂的机器学习算法，在语音和图像识别方面取得的效果，远远超过先前相关技术。

深度学习在搜索技术、数据挖掘、机器学习、机器翻译、自然语言处理、多媒体学习、语音、推荐和个性化技术，以及其他相关领域都取得了很多成果。深度学习使机器模仿视听和思考等人类的活动，解决了很多复杂的模式识别难题，使得人工智能相关技术取得了很大进步。

5. 应用

机器学习应用广泛，无论是在军事领域还是民用领域，都有机器学习算法施展的机会，主要包括以下几个方面。

5.1 数据分析与挖掘

“数据挖掘”和"数据分析”通常被相提并论，并在许多场合被认为是可以相互替代的术语。关于数据挖掘，已有多种文字不同但含义接近的定义，例如“识别出巨量数据中有效的.新颖的、潜在有用的最终可理解的模式的非平凡过程”，无论是数据分析还是数据挖掘，都是帮助人们收集、分析数据，使之成为信息，并做出判断，因此可以将这两项合称为数据分析与挖掘。

数据分析与挖掘技术是机器学习算法和数据存取技术的结合，利用机器学习提供的统计分析、知识发现等手段分析海量数据，同时利用数据存取机制实现数据的高效读写。机器学习在数据分析与挖掘领域中拥有无可取代的地位，2012年Hadoop进军机器学习领域就是一个很好的例子。

5.2 模式识别

模式识别起源于工程领域，而机器学习起源于计算机科学，这两个不同学科的结合带来了模式识别领域的调整和发展。模式识别研究主要集中在两个方面。

（1）研究生物体（包括人）是如何感知对象的，属于认识科学的范畴。

（2）在给定的任务下，如何用计算机实现模式识别的理论和方法，这些是机器学习的长项，也是机器学习研究的内容之一。

模式识别的应用领域广泛，包括计算机视觉、医学图像分析、光学文字识别、自然语言处理、语音识别、手写识别、生物特征识别、文件分类、搜索引擎等，而这些领域也正是机器学习大展身手的舞台，因此模式识别与机器学习的关系越来越密切。

5.3 在生物信息学上的应用

随着基因组和其他测序项目的不断发展，生物信息学研究的重点正逐步从积累数据转移到如何解释这些数据。在未来，生物学的新发现将极大地依赖于我们在多个维度和不同尺度下对多样化的数据进行组合和关联的分析能力，而不再仅仅依赖于对传统领域的继续关注。序列数据将与结构和功能数据基因表达数据、生化反应通路数据表现型和临床数据等一系列数据相互集成。如此大量的数据，在生物信息的存储、获取、处理、浏览及可视化等方面，都对理论算法和软件的发展提出了迫切的需求。另外，由于基因组数据本身的复杂性也对理论算法和软件的发展提出了迫切的需求。而机器学习方法例如神经网络、遗传算法、决策树和支持向量机等正适合于处理这种数据量大、含有噪声并且缺乏统一理论的领域。

5.4 更广阔的领域

国外的IT巨头正在深入研究和应用机器学习，他们把目标定位于全面模仿人类大脑，试图创造出拥有人类智慧的机器大脑。

2012年Google在人工智能领域发布了一个划时代的产品一人脑模拟软件，这个软件具备自我学习功能。模拟脑细胞的相互交流，可以通过看YouTube视频学习识别猫、人以及其他事物。当有数据被送达这个神经网络的时候，不同神经元之间的关系就会发生改变。而这也使得神经网络能够得到对某些特定数据的反应机制，据悉这个网络已经学到了一些东西，Google将有望在多个领域使用这一新技术，最先获益的可能是语音识别。

5.5 具体应用

（1）虚拟助手。Siri，Alexa，Google Now都是虚拟助手。顾名思义，当使用语音发出指令后，它们会协助查找信息。对于回答，虚拟助手会查找信息，回忆我们的相关查询，或向其他资源（如电话应用程序）发送命令以收集信息。我们甚至可以指导助手执行某些任务，例如“设置7点的闹钟”等。

（2）交通预测。生活中我们经常使用GPS导航服务。当我们这样做时，我们当前的位置和速度被保存在中央服务器上来进行流量管理。之后使用这些数据用于构建当前流量的映射。通过机器学习可以解决配备GPS的汽车数量较少的问题，在这种情况下的机器学习有助于根据估计找到拥挤的区域。

（3）过滤垃圾邮件和恶意软件。电子邮件客户端使用了许多垃圾邮件过滤方法。为了确保这些垃圾邮件过滤器能够不断更新，它们使用了机器学习技术。多层感知器和决策树归纳等是由机器学习提供支持的一些垃圾邮件过滤技术。每天检测到超过325000个恶意软件，每个代码与之前版本的90%～98%相似。由机器学习驱动的系统安全程序理解编码模式。因此，他们可以轻松检测到2%～10%变异的新恶意软件，并提供针对它们的保护。

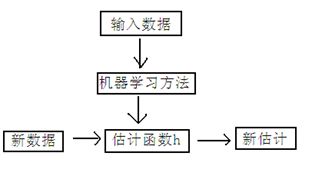
6. 数据学习开发流程

1.获取数据

2.数据处理

3.特征工程

4.机器学习算法训练 - 模型

5.模型评估

6.应用

7. 学习目标

算法是核心，数据是计算是基础

分析很多的数据

分析具体的业务

应用常见的算法

8. 数据集

8.1 数据集

8.1.1 可用数据集

公司内部，百度

数据接口、花钱

数据集

Kaggle大数据竞赛平台，80万科学家，真实数据，数据量大。

UCI收集了360个数据集，覆盖科学、生活、经济领域。

scikit-learn数据量小，方便学习

9. Python数据分析工具介绍

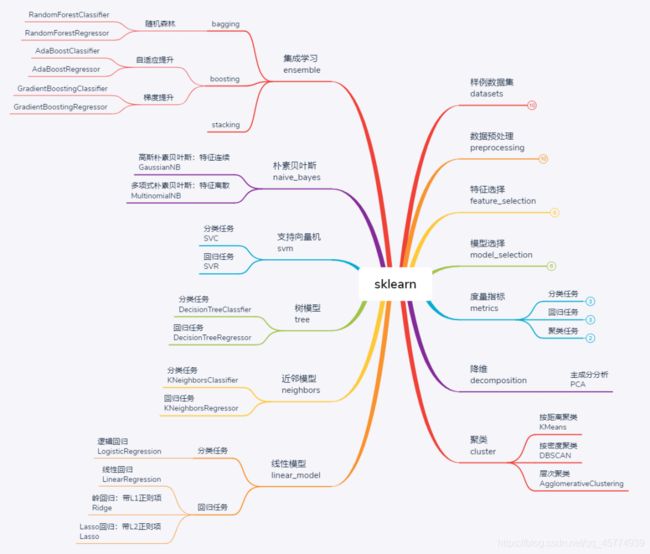
9.1 Scikit-learn工具介绍

机器学习工具；

机器学习算法语言丰富；

完善、稳定

包含：分类、回归、聚类、降维、、调优、模型选择、特征工程。

9.3 Scikit-learn数据集api介绍

sklearn.datasets

加载获取流行数据集

datasets.load_*()获取小规模数据集

datasets.fetch_*(data_home-None)获取大规模数据集

datasets.base.bunch(继承自字典)

dict['key']=values(用字典获取返回值)

bunch.key=values

返回值特征：

data：特征数据数组，是[n_samples*n_features]的二维np.ndarray数组

target: 标签数组，一维数组

DESCR：数据描述

feature_names:特征名.新闻数据

target_names:标签名

eg:

import sklearn.datasets as datasets

# print(iris)
def datasets_down():
    """
    sklearn数据集的使用
    :return:
    """
    iris = datasets.load_iris()
    print(iris)
    print(iris['DESCR'])
    print('名字:\n',iris.target_names)
    return None
if __name__ == '__main__':
    datasets_down()

9.4 数据集的划分

一般划分为两个部分：

训练部分：用于训练，构建模型

测试部分：在模型检验使用，用于评估模型是否有效。

划分比例：

训练集：70%，80%，90%

测试集：30%，20%，10%

#导入数据包
from sklearn.model_selection import train_test_split
#划分数据集（x,y,test_size,random_state,return）
X_train,x_test,y_train,y_test=train_test_split(data,target,test_size=0.1)
# 训练
knn = KNeighborsClassifier()
knn.fit(X_train,y_train)
# 预测
knn.predict(x_test)
y_test#对照组

10.特征工程

10.1 定义

特征工程往往是打开数据密码的钥匙，是数据科学中最有创造力的一部分。因为往往和具体的数据相结合，很难优雅地系统地讲好。所以课本上会讲一下理论知识比较扎实的归一化，降维等部分，而忽略一些很dirty hand的特征工程技巧。特征工程，顾名思义，是对原始数据进行一系列工程处理，将其提炼为特征，作为输入供算法和模型使用。

10.2 模块流程

10.2.1 特征抽取

机器学习-统计学-数学

文本—》数字？

#身高、体重、鞋子尺码数据对应性别
#需要训练数据
X_train = np.array([[180,80,43],[160,50,37],[175,55,42],[160,60,40],[160,50,37],[185,85,44]])
y_lables = np.array(['男','女','男','女','女','男'])
# 生成knn算法的实例
knn = KNeighborsClassifier()
# 训练
knn.fit(X_train,y_lables)
# 预测
# 测试数据
x_test = np.array([[160,48,38]])
knn.predict(x_test)
x_test = np.array([[178,80,43],[160,48,37],[175,54,42],[160,60,40],[160,50,37],[185,85,44]])
knn.predict(x_test)

将数据转换为可用的数字特征（相当于标签化）

字典特征提取（特征离散化）

文本特征提取

图像特征提取（深度学习介绍）

特征提取API

sklearn.feature_extraction

10.2.1.1字典特征提取

*sklearn.feature_extraction.DivtVectorize(sparse=True...)*

1. DivtVectorize.fit_transform(X) X:字典或者包含字典的迭代器返回值：返回sparse矩阵

2. DivtVectorize.inverse_transform(X) X:array数组或者sparse矩阵，转换之前的数据格式

3. DivtVectorize.get_feature_name()返回类别名称

eg：

[{'city':'北京','temperature':100},{'city':'上海','temperature':60},{'city':'深圳','temperature':30}]

from sklearn.feature_extraction import DictVectorizer
data=[{'city':'北京','temperature':100},{'city':'上海','temperature':60},{'city':'深圳','temperature':30}]
    # 实例化一个转换器
    transform =DictVectorizer() # sparse=True/False
    # 调用fit_transform()
    data_new=transform.fit_transform(data)
    print(data_new)# 返回稀疏矩阵

应用场景：

数据集中有很多类别特征

本身拿到的数据为字典特征抽取

10.2.1.1文本特征提取

单词作为特征：特征词

句子、短语、字母

方法一：*sklearn.feature_extraction.text.CountVectorize(stop_words=[]…)*返回词频矩阵

CountVectorize.fit_transform(X) X:字典或者包含字典的迭代器返回值：返回sparse矩阵
CountVectorize.inverse_transform(X) X:array数组或者sparse矩阵，转换之前的数据格式
CountVectorize.get_feature_name()返回单词名称

sklearn.feature_extraction.text.TfidfVectorize

应用：

from sklearn.feature_extraction.text import CountVectorizer
def text_demo():
    """
    文本特征抽取
    :return:
    """
    data = ['To an optimist every change is a change for the better', 'Saying and doing are two different things']
    # 实例化一个转换器
    transfer = CountVectorizer(stop_words=[])

    # 调用fit_transform()
    data_new = transfer.fit_transform(data)
    print(data_new.toarray())  # 统计单词出现的个数
    print(transfer.get_feature_names())
    return None


def china_demo():
    """
    文本特征抽取
    :return:
    """
    data = ['一个人最大的敌人就是他自己', '遭祸容易脱祸难']
    # 实例化一个转换器
    transfer = CountVectorizer(stop_words=[])

    # 调用fit_transform()
    data_new = transfer.fit_transform(data)
    print(data_new.toarray())  # 统计单词出现的个数
    print(transfer.get_feature_names())
    return None
def cut_word(text):
    """
    中文分词，jieba.join
    :param text:
    :return:
    """

    return "/".join(list(jieba.cut(text,cut_all=True)))
def china_demo2():
    """
    文本特征抽取，自动分词
    :return:
    """
    data = ['一个人最大的敌人就是他自己', '遭祸容易脱祸难']
    data_new=[]
    for sent in data:
        data_new.append(cut_word(sent))
    # print(data_new)
    # 实例化一个转换器
    transfer = CountVectorizer(stop_words=[])
    # 调用fit_transform()
    data_new2 = transfer.fit_transform(data_new)
    print(data_new2.toarray())  # 统计单词出现的个数
    print(transfer.get_feature_names())



    return None
if __name__ == '__main__':
    # print(cut_word("我爱北京天安门"))
    china_demo2()

方法二：TfidfVectorizer

TF-IDF（term frequency–inverse document frequency，词频-逆向文件频率）是一种用于信息检索（information retrieval）与文本挖掘（text mining）的常用加权技术。

关键词判断文章类型，用于评估一个词对于一个文件集或者一个语料库中的其中一份文件的重要程度。

TF是词频(Term Frequency)

IDF是逆向文件频率(Inverse Document Frequency)

方法：Tf-idf

1000篇文章-“运行库”

100篇文章-“非常”

10篇文章-“帅气”

文章（1000库）：10次“帅气”

$t f : 10 / 100 = 0.1 i d f = l o g 101000 / 10 = 2 t f - i d f = 2 * 0.1 = 0.2$
文章（1000库）：100次“非常”

$$
tf:10/100=0.1

idf=log10 1000/100=1

tf-idf=2*0.1=0.1
$$

from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
def china_demo3():
    """
    文本特征抽取，自动分词
    :return:
    """
    data = ['我一个所能奉献的没有其它，只有热血、辛劳、眼泪与汗水','对聪明人来说，每一天的时间都是要精打细算的','一个人最大的敌人就是他自己', '遭祸容易脱祸难']
    data_new=[]
    for sent in data:
        data_new.append(cut_word(sent))
    # print(data_new)
    # 实例化一个转换器
    transfer = TfidfVectorizer(stop_words=['一个'])
    # 调用fit_transform()
    data_new2 = transfer.fit_transform(data_new)
    print(data_new2.toarray())  # 统计单词出现的个数
    print(transfer.get_feature_names())
    return None
if __name__ == '__main__':
    # print(cut_word("我爱北京天安门"))
    china_demo3()

10.2.2 特征预处理

包含内容

数据值数据的无量纲化:数据的规格不一，导致结果不一样。

10.2.2.1.归一化（方法不止这一种）

通过对原始数据的变换将数据映射在[0,1]之间.把有量纲表达式变为无量纲表达式，解决数据的可比性。

1.2.方法

min-max标准化

通过遍历feature vector里的每一个数据，将Max和Min的记录下来，并通过Max-Min作为基数（即Min=0，Max=1）进行数据的归一化处理：其中Max为样本数据的最大值，Min为样本数据的最小值。

sklearn：API

sklearn.preprocessing.MinMaxScaier(feature_range=(0,1)...)
	MinMaxScaler.fit_transform(x)
		X:numpy.array
	返回值：转换后形状相同的array

自定义函数

def MaxMinNormalization(x,Max,Min):
x = (x - Min) / (Max - Min);
 
return x;

缺点：容易受到异常数影响

def min_max():
    """
    min-max标准化数据预处理
    :return:
    """
    data = pd.read_csv('datingTestSet.txt', sep='\t')
    data.columns = ['milage', 'Liters', 'Consumtime', 'target']
    # print(data)
    data1 = data.iloc[:, :3]
    # print(data1)
    # 实例化一个转换器
    transfer = MinMaxScaler(feature_range=(2, 3))
    # 调用fit_transform()
    data_new3 = transfer.fit_transform(data1)
    print(data_new3)
    return None

10.2.2.1.标准化

（x-mean）/std(标准差：集中程度)

API

sklearn.preprocessing.StandardScaler()

	处理以后，每列数据都集中在均值为0附近，标准差为1

		StandardScaler.fit_transform(x)

			X:numpy.array
	返回值：转换后形状相同的array

def Standard_Scaler():
    """
   Standard_Scaler标准化数据预处理
    :return:
    """
    data = pd.read_csv('../data/datingTestSet.txt', sep='\t')
    data.columns = ['milage', 'Liters', 'Consumtime', 'target']
    # print(data)
    data1 = data.iloc[:, :3]
    # print(data1)
    # 实例化一个转换器
    transfer = StandardScaler()
    # 调用fit_transform()
    data_new3 = transfer.fit_transform(data1)
    print(data_new3)
    return None

10.2.3 特征降维

在特定条件下，降低随机变量的个数，得到一组‘不相关’主变量的过程。

ndarray

维数：嵌套的层数。

0维：标量

1维：向量

2维：矩阵

3维：

n维：

二维数组

其实是特征的个数降低。

特性分为：相关特征，不相关特征。由于特征本身的相关性较强，对于算法学习与预测的影响比较大。

10.2.3.1 特征选择

是数据中包含冗余或者相关变量。

.Filter(过滤式)
方差分析法：低方差特征过滤
- 特征方差小：
- 特征方差大

API

sklearn.feature_selection.Variance Threshold(Threshold=5)

+ 删除低方差的特征（Threshold=5设定方差值低于5的删除）
+ Variance .fit.transform(X)
+ X:numpy.array格式的数据特征将被删除，默认值是保留所有非零方差的特征，即删除所有样本中具有相同值的特征。

from sklearn.feature_selection import VarianceThreshold
def variance_demo():
    """
    过滤低方差特征
    :return:
    """
    data = pd.read_csv('../data/factor_returns.csv')
    data = data.iloc[:, 1:-2]
    # 实例化一个转换器类
    transfer = VarianceThreshold(threshold=5)
    # 调用fit_transform()
    data_new = transfer.fit_transform(data)
    print(data_new.shape)
    return None

相关系数：特征之间的相关性
- 皮尔逊相关系数：反映变量之间的相关关系密切程度
公式：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C5ypTKp3-1626744212559)(C:\Users\Administrator\Desktop\19961_1278838271Lch3.gif)]

如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：

(1)、当相关系数为0时，X和Y两变量无关系。
(2)、当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间。
(3)、当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间。

相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。

通常情况下通过以下取值范围判断变量的相关强度：
相关系数

0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关

from scipy.stats import pearsonr

+ x:(N)array_like
+ y:(N)array_like Returns: pearsonr's p-valus
+ pearsonr(x,y)

from sklearn.feature_selection import VarianceThreshold
def variance_demo():
    """
    过滤低方差特征
    :return:
    """
    data = pd.read_csv('../data/factor_returns.csv')
    data = data.iloc[:, 1:-2]
    # 实例化一个转换器类
    transfer = VarianceThreshold(threshold=5)
    # 调用fit_transform()
    data_new = transfer.fit_transform(data)
    print(data_new.shape)
    #相关性值获取Pear_sonr=pearsonr(data['pe_ratio'],data['pd_ratio'])
    print(Pear_sonr)
    return None

2.Eabeded（嵌入式）

决策树

正则化

深度学习

10.2.3.2 主成分分析（PCA）

定义：主成分分析（Principal Component Analysis，PCA），是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分

PCA降维的目的，就是为了在尽量保证“信息量不丢失”的情况下，对原始特征进行降维，也就是尽可能将原始特征往具有最大投影信息量的维度上进行投影。将原特征投影到这些维度上，使降维后信息量损失最小。

应用于回归分析、聚类分析中。

求解步骤

去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值排序
保留前N个最大的特征值对应的特征向量
将原始特征转换到上面得到的N个特征向量构建的新空间中（最后两步，实现了特征压缩）

API

API
+ sklearn.decomposition.PCA（n_components=None)
+ 将数据分解为较低维数空间
+ n_components
  + 小数：保留百分之多少的信息
  + 整数：减少到多少特征
+ PCA.fit_transform(X)X:numpy.array格式的数据
+ 返回值：转换后指定维度的array

案例分析

1. insta_cart市场篮子分析

import pandas as pd
from sklearn.decomposition import PCA

aisles = pd.read_csv("./instacart/aisles.csv")
orders = pd.read_csv("./instacart/orders.csv")
products = pd.read_csv("./instacart/products.csv")
order_products__prior = pd.read_csv("./instacart/order_products__prior.csv")
# pd.set_option('display.max_columns', 100)
# pd.set_option('display.width', 500)
# print(order_products__prior)
# print(aisles)
# print(orders)
# print(products)
# def instacart_aly():
# 合并aisles、products表
tab1 = pd.merge(aisles, products, on=['aisle_id', 'aisle_id'])
# print(tab1)
# 合并tab1、order_products__prior表
tab2 = pd.merge(tab1, order_products__prior, on=['product_id', 'product_id'])
# print(tab2)
# 合并tab2、orders.csv表
tab3 = pd.merge(tab2, orders, on=['order_id', 'order_id'])
# print(tab3.head())
tab4 = pd.crosstab(tab3['user_id'], tab3['aisle'])
tab5 = tab4[:10000]
transfer = PCA(n_components=0.95)
data_new = transfer.fit_transform(tab5)
print(data_new)

11. 分类算法

目标值：类别

11.1 sklearn的转换器和预估器

11.1.1转换器

实例化
调用fit_transform()
- fit() 计算每一列的平均值、标准差
- transform() （x-mean）/std 转换到公式

eg:（x-mean）/std

11.1.2预估器

实例化一个estimator
estimator.fit(x_train,y_train) 计算，调用，模型生成
模型评估
- 直接比对真实值和预测值
  - y_predict=estimator.predict(x_test)
  - y_predic(预测值)==y_test(真实值)
- 计算准确率
- estimator.score(x_test,y_test)

11.2 KNN算法

11.2.1 什么是KNN算法

定义
- K最近邻（KNN，K-NearestNeighbor）分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻，就是K个最近的邻居的意思，说的是每个样本都可以用它最接近的K个邻近值来代表。近邻算法就是将数据集合中每一个记录进行分类的方法
步骤
- 总体来说，KNN分类算法包括以下4个步骤：
  - ①准备数据，对数据进行预处理。
  - ②计算测试样本点（也就是待分类点）到其他每个样本点的距离。
  - ③对每个距离进行排序，然后选择出距离最小的K个点。
  - ④对K个点所属的类别进行比较，根据少数服从多数的原则，将测试样本点归入在K个点中占比最高的那一类
算法：欧式距离

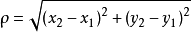
11.2.2 KNN算法API

from sklearn.neighbors import KNeighborsClassifier
def KNeighborsClassifier(n_neighbors = 5,
                       weights='uniform',
                       algorithm = '',
                       leaf_size = '30',
                       p = 2,
                       metric = 'minkowski',
                       metric_params = None,
                       n_jobs = None
                       )
										
- n_neighbors：这个值就是指 KNN 中的 “K”了。前面说到过，通过调整 K 值，算法会有不同的效果。K值过小，容易受到异常点的影响。k值过大，会受到样本不平衡的影响。
- weights（权重）：最普遍的 KNN 算法无论距离如何，权重都一样，但有时候我们想搞点特殊化，比如距离更近的点让它更加重要。这时候就需要 weight 这个参数了，这个参数有三个可选参数的值，决定了如何分配权重。参数选项如下：
        • 'uniform'：不管远近权重都一样，就是最普通的 KNN 算法的形式。
        • 'distance'：权重和距离成反比，距离预测目标越近具有越高的权重。
        • 自定义函数：自定义一个函数，根据输入的坐标值返回对应的权重，达到自定义权重的目的。
- algorithm：在 sklearn 中，要构建 KNN 模型有三种构建方式，1. 暴力法，就是直接计算距离存储比较的那种放松。2. 使用 kd 树构建 KNN 模型 3. 使用球树构建。 其中暴力法适合数据较小的方式，否则效率会比较低。如果数据量比较大一般会选择用 KD 树构建 KNN 模型，而当 KD 树也比较慢的时候，则可以试试球树来构建 KNN。参数选项如下：
		• 'brute' ：蛮力实现
		• 'kd_tree'：KD 树实现 KNN
		• 'ball_tree'：球树实现 KNN 
		• 'auto'： 默认参数，自动选择合适的方法构建模型
不过当数据较小或比较稀疏时，无论选择哪个最后都会使用 'brute'
		
- leaf_size：如果是选择蛮力实现，那么这个值是可以忽略的，当使用KD树或球树，它就是是停止建子树的叶子节点数量的阈值。默认30，但如果数据量增多这个参数需要增大，否则速度过慢不说，还容易过拟合。
- p：和metric结合使用的，当metric参数是"minkowski"的时候，p=1为曼哈顿距离， p=2为欧式距离。默认为p=2。
- metric：指定距离度量方法，一般都是使用欧式距离。
		• 'euclidean' ：欧式距离
		• 'manhattan'：曼哈顿距离
		• 'chebyshev'：切比雪夫距离
		• 'minkowski'： 闵可夫斯基距离，默认参数
- n_jobs：指定多少个CPU进行运算，默认是-1，也就是全部都算。

11.2.3 案例：莺尾花种类预测


def datasets_down():
    """
    sklearn数据集的使用
    :return:
    """
    iris = datasets.load_iris()
    # print(iris.data)
    # print(iris)
    # print(iris['DESCR'])
    # print('名字:\n',iris.target_names)
    # 划分数据集（x,y,test_size,random_state,return）
    X_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.1)
    # print(X_train)
    # print(y_train)
    # 标准化
    transfer=StandardScaler()
    X_train=transfer.fit_transform(X_train)
    # print(x_test)
    # x_test=transfer.transform(x_test)
    # print(x_test)
    #
    knn = KNeighborsClassifier()
    # 训练
    knn.fit(X_train, y_train)
    # 预测
    X_test01 = knn.predict(x_test)
    # print(X_test01)
    # print(y_test)
    knn.score(x_test, y_test)  # 返回R的次方
    knn.score(X_train, y_train)  # 返回R的次方
    # c = target 分类
    plt.scatter(iris.data[:, 0], iris.data[:, 1], c=iris.target, cmap='rainbow')
    plt.show()

    # 定义KNN分类器
    # knn = KNeighborsClassifier()
    # print(iris.data.shape)
    # print(iris.target.shape)
    # print(iris.data[:,:2])

    return None

11.2.4 KNN算法总结

优点：KNN方法思路简单，易于理解，易于实现，无需估计参数
缺点：当样本不平衡时，大容量样本的K个邻居中大容量类的样本占多数；计算量较大。

11.3 模型选择与调优

11.3.1 什么是交叉验证

定义：将数据划分为训练集与测试集。均分交叉验证。交叉验证既可以解决数据集的数据量不够大问题，也可以解决参数调优的问题。这块主要有三种方式：简单交叉验证（HoldOut检验）、k折交叉验证（k-fold交叉验证）、自助法。该文仅针对k折交叉验证做详解。
简单交叉验证
- 方法：将原始数据集随机划分成训练集和验证集两部分。比如说，将样本按照70%~30%的比例分成两部分，70%的样本用于训练模型；30%的样本用于模型验证.
k折交叉验证
- 1、首先，将全部样本划分成k个大小相等的样本子集；
- 2、依次遍历这k个子集，每次把当前子集作为验证集，其余所有样本作为训练集，进行模型的训练和评估；
- 3、最后把k次评估指标的平均值作为最终的评估指标。在实际实验中，k通常取10.
- 举个例子：这里取k=10，如下图所示：
  （1）先将原数据集分成10份
  （2）每一将其中的一份作为测试集，剩下的9个（k-1）个作为训练集此时训练集就变成了k * D（D表示每一份中包含的数据样本数）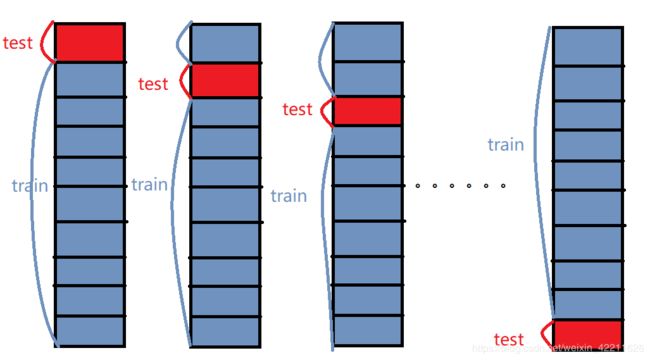
  
  （3）最后计算k次求得的分类率的平均值，作为该模型或者假设函数的真实分类率
  
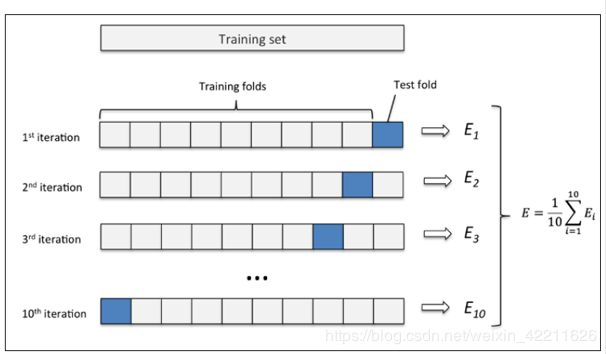
  交叉验证的方式，要简单于数学理解，而且具有说服性。需要谨记一点，当样本总数过大，若使用留一法时间开销极大。
自主法
- 自助法是基于自助采样法的检验方法。对于总数为n的样本合集，进行n次有放回的随机抽样，得到大小为n的训练集。
- n次采样过程中，有的样本会被重复采样，有的样本没有被抽出过，将这些没有被抽出的样本作为验证集，进行模型验证。

11.3.2 超参数搜索-网格搜索

超参数搜索定义
- 超参数是在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。通常情况下，在机器学习过程中需要对超参数进行优化，给学习器选择一组最优超参数，以提高学习的性能和效果。比如，树的数量或树的深度，学习率（多种模式）以及k均值聚类中的簇数等都是超参数。
参数
- 与超参数区别的概念是参数，它是模型训练过程中学习到的一部分，比如回归系数，神经网络权重等。简单的描述参数是模型训练获得的，超参数是人工配置参数（本质上是参数的参数，每次改变超参数，模型都要重新训练）。
超参数调优
- 在模型训练过程中的参数最优化，一般都是对参数的可能值进行有效搜索，然后用评价函数选取出最优参数，比如梯度下降法。
- 同理，人工的超参数选择过程，我们也可以采取类似参数搜索的办法，来提高效率，如果进行人工试错的方式，会非常浪费时间。
- 流程
  - 超参数搜索过程：
    - 将数据集分为训练集，验证集及测试集。
    - 选择模型性能评价指标
    - 用训练集对模型进行训练
    - 在验证集上对模型进行参数进行搜索，用性能指标评价参数好坏
    - 选出最优参数
    常见超参数搜索算法：
    - 网格搜索
    - 随机搜索
    - 启发式搜索
网格搜索
- 网格搜索是在所有候选的参数选择中，通过循环遍历，尝试每一种可能性，表现最好的参数就是最终的结果（暴力搜索）。
- 原理：
  - 在一定的区间内，通过循环遍历，尝试每一种可能性，并计算其约束函数和目标函数的值，对满足约束条件的点，逐个比较其目标函数的值，将坏的点抛弃，保留好的点，最后便得到最优解的近似解。
  - 为了评价每次选出的参数的好坏，我们需要选择评价指标，评价指标可以根据自己的需要选择accuracy、f1-score、f-beta、percision、recall等。
  - 同时，为了避免初始数据的划分对结果的影响，我们需要采用交叉验证的方式来减少偶然性，一般情况下网格搜索需要和交叉验证相结合使用。
网格搜索API

GridSearchCV(
estimator,
param_grid, 
scoring=None, 
fit_params=None, 
n_jobs=1, 
iid=True, 
refit=True,
cv=None, 
verbose=0, 								pre_dispatch='2*n_jobs', 
error_score='raise',
return_train_score=True)

estimator：所使用的分类器
param_grid：值为字典或者列表，需要最优化的参数的取值范围，如paramters = {'n_estimators':range(10,100,10)}。
scoring :准确度评价指标，默认None,这时需要使用score函数；或者如scoring='roc_auc'。
fit_params:字典类型数据，主要用于给fit方法传递参数。
n_jobs: 并行数，int：个数,-1：跟CPU核数一致, 1:默认值。
pre_dispatch：指定总共分发的并行任务数。当n_jobs大于1时，数据将在每个运行点进行复制，这可能导致OOM，而设置pre_dispatch参数，则可以预先划分总共的job数量，使数据最多被复制pre_dispatch次。
iid:默认True,为True时，默认为各个样本fold概率分布一致，误差估计为所有样本之和，而非各个fold的平均。
cv :交叉验证参数，默认None，使用三折交叉验证。指定fold数量，默认为3，也可以是yield训练/测试数据的生成器。
refit :默认为True,程序将会以交叉验证训练集得到的最佳参数，重新对所有可用的训练集与验证集进行训练，作为最终用于性能评估的最佳模型参数。即在搜索参数结束后，用最佳参数结果再次fit一遍全部数据集。
verbose：日志冗长度，int：冗长度，0：不输出训练过程，1：偶尔输出，>1：对每个子模型都输出。
error_score: 默认为raise，可选择参数numeric，在模型拟合过程中如果产生误差，在raise情况下，误差分数将会提高，如果选择numeric，则fitfailedwarning会提高。
return_train_score:布尔类型数据，默认为Ture ,为False时交叉验证的结果不包含训练得分。

结果分析：

最佳参数：best_params_
最佳结果：best_score_
最佳估计器：best_estimator_
交叉验证结果：cv_results_

11.3.3 鸢尾花案例加k值调优

def datasets_down():
    """
    鸢尾花加上k值调优
    :return:
    """
    iris = datasets.load_iris()
    # print(iris.data)
    # print(iris)
    # print(iris['DESCR'])
    # print('名字:\n',iris.target_names)
    # 划分数据集（x,y,test_size,random_state,return）
    X_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.1)
    # 标准化
    transfer = StandardScaler()
    X_train = transfer.fit_transform(X_train)
    # 实例化
    knn = KNeighborsClassifier()
    # 加入网格搜索与交叉验证
    # 参数准备
    param_dict={'n_neighbors':[1,3,5,7,9,11]}
    knn=GridSearchCV(knn,param_grid=param_dict,cv=10)
    # 训练
    knn.fit(X_train, y_train)
    # 预测
    X_test01 = knn.predict(x_test)
    knn.score(x_test, y_test)  # 返回R的次方
    knn.score(X_train, y_train)  # 返回R的次方
    print(knn.best_params_)
    print(knn.best_score_)
    print(knn.best_estimator_)
    print(knn.cv_results_)
    plt.scatter(iris.data[:, 0], iris.data[:, 1], c=iris.target, cmap='rainbow')
    plt.show()

    return None

11.3.4 预测fecebook签到

# 流程：
# 获取数据
# 数据处理
# 目的：特征值、目标值：缩小数据范围（利用数据表筛选数值），处理时间戳
# 特征工程
# KNN算法预估流程
# 模型选择与调优
# 模型评估

#%%
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import cross_val_score, GridSearchCV, train_test_split
#%%


data0=pd.read_csv('./data/FBlocation/test.csv')
data1=pd.read_csv('./data/FBlocation/train.csv')

#%%
data1.head()
# 流程：
# 获取数据
# 数据处理
# 目的：特征值、目标值：缩小数据范围（利用数据表筛选数值），处理时间戳
# 特征工程
# KNN算法预估流程
# 模型选择与调优
# 模型评估
#%%
# 数据处理-1：缩小数据范围
data1=data1.query('x<2.5 & x>2 & y<1.5 & y>1.0')
#%%
# 数据处理-2：处理时间戳
time_values=pd.to_datetime(data1['time'],unit='s')
# time_values.values
date=pd.DatetimeIndex(time_values)
date.weekday
#%%增加时间特征值
data1['day']=date.day
data1['weekday']=date.weekday
data1['hour']=date.hour

#%%
data1
#%% 过滤签到次数少的地点
place_count=data1.groupby('place_id').count()['row_id']
# place_count[place_count>3]
data1_final=data1[data1['place_id'].isin(place_count[place_count>3].index.values)]
#%%
data1_final
#%% 筛选特征值与测试值
xx=data1_final[['x','y','accuracy','day','weekday','hour']]
yy=data1_final['place_id']
#%% 数据集划分
x_train,x_test,y_train,y_test=train_test_split(xx,yy)
x_train
#%% 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
# 实例化
knn = KNeighborsClassifier()
# 加入网格搜索与交叉验证
# 参数准备
param_dict={'n_neighbors':[1,3,5,7,9,11]}
knn=GridSearchCV(knn,param_grid=param_dict,cv=10)
# 训练
knn.fit(x_train, y_train)
# 预测
X_test01 = knn.predict(x_test)
knn.score(x_test, y_test)  # 返回R的次方
knn.score(x_train, y_train)  # 返回R的次方
print(knn.best_params_)
print(knn.best_score_)
print(knn.best_estimator_)
print(knn.cv_results_)

#%%
# type(yy)
plt.scatter(xx.values[:, 0], xx.values[:, 1], c=yy.values, cmap='rainbow')
plt.show()

11.3.5 总结

优点：增加可信度
缺点：
- （1）数据都只被所用了一次，没有被充分利用
- （2）在验证集上计算出来的最后的评估指标与原始分组有很大关系。

11.4 朴素贝叶斯算法

11.4.1 定义

朴素贝叶斯模型是一个简单快速的分类算法，适用于维度较高的的数据集，因为它可调的参数少，运行速度快，所以多用于初步的数据分类。它基于 “ 贝叶斯定理 ” 而得名，是关于随机事件 A 和 B 的条件概率的数学定理。其中 P(A|B）是在 B 发生的情况下 A 发生的可能性。这个数学定理十分有趣，并且跟生活有着密切的关联。

11.4.2 概率基础

定义
- 概率，亦称“或然率”，它是反映随机事件出现的可能性大小。
概率具有以下7个不同的性质：

性质1：
$p (x) = 0$
性质2：（有限可加性）当n个事件A1,…,An两两互不相容时：　

性质3：对于任意一个事件A：

性质4：当事件A,B满足A包含于B时：

性质5：对于任意一个事件A，

性质6：对任意两个事件A和B，

性质7：（加法公式）对任意两个事件A和B，

11.4.3 联合概率、条件概率、与相互独立

联合概率
- 指在多元的概率分布中多个随机变量分别满足各自条件的概率。假设X和Y都服从正态分布，那么P{X<4,Y<0}就是一个联合概率，表示X<4,Y<0两个条件同时成立的概率。表示两个事件共同发生的概率。A与B的联合概率表示为 P(AB) 或者P(A,B),或者P（A∩B）。
条件概率
- 指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为：P（A|B），读作“在B的条件下A的概率”。条件概率可以用决策树进行计算。条件概率的谬论是假设 P(A|B) 大致等于 P(B|A)。数学家John Allen Paulos 在他的《数学盲》一书中指出医生、律师以及其他受过很好教育的非统计学家经常会犯这样的错误。这种错误可以通过用实数而不是概率来描述数据的方法来避免。
相互独立
- 设A,B是两事件,如果满足等式P(AB)=P(A)P(B),则称事件A,B相互独立,简称A,B独立.

11.4.4 贝叶斯公式

公式中，事件y的概率为P(y)，事件y已发生条件下事件x的概率为P(x│y)，事件x发生条件下事件y的概率为P(y│x)。

API
- *sklearn.naive_bayes.MultinomialNB*
  
  sklearn.naive_bayes.MultinomialNB(alpha = 1.0) 朴素贝叶斯分类
  
  alpha：拉普拉斯平滑系数
拉普拉斯平滑系数
- 当我们在使用朴素贝叶斯算法去解决分类问题时，在训练集上进行训练时我们可以发现有可能出现某些特征的概率P为0的情况，无论是在全文检索中某个字出现的概率，还是在垃圾邮件分类中，这种情况明显是不太合理的，不能因为一个事件没有观察到就武断的认为该事件的概率是0，拉普拉斯的理论支撑而拉布拉斯平滑处理正是处理这种情况下应运而生的。
- 而我们可以发现如果当训练样本集很大的时候，我们讲每个样本值加1，这样造成的估计概率变化并不大，完全在我们可以接受的范围内，而拉普拉斯平滑处理的思想就是将样本值加1，来对数据集进行平滑处理。
- p（Fi|C）=(Ni+alpha)/(N+alpha*m)
  alpha是指定的系数一般是1，m是训练文档中统计出来的特征词的个数。
  
  API：sklearn.naive_bayes.MultinomiaLNB(alpha=1.0)默认平滑系数1.0

11.4.6 案例：20类新闻分类

# -*- coding: utf-8 -*-
# @Time    : 2021/7/14 19:47
# @Author  : long
# @Email   : [email protected]
# @File    : 机器学习分类算法贝叶斯专项.py
# @Software: PyCharm
import pandas as pd
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB


def nb_news():
    """
    20类新闻分类:朴素贝叶斯
    :return:
    """
    # 获取数据
    news = fetch_20newsgroups()
    # 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target)
    # 特征工程：文本特征抽取
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 朴素贝叶斯算法预估器流程
    estimator = MultinomialNB(alpha=1.0)
    estimator.fit(x_train, y_train)
    # 模型评估
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("对比:\n", y_test == y_predict)
    score = estimator.score(x_test, y_test)  # 返回R的次方
    print('准确率为:\n', score)
    return None


if __name__ == '__main__':
    nb_news()

11.4.7 朴素贝叶斯算法总结

优点
- 朴素贝叶斯算法假设了数据集属性之间是相互独立的，因此算法的逻辑性十分简单，并且算法较为稳定，当数据呈现不同的特点时，朴素贝叶斯的分类性能不会有太大的差异。换句话说就是朴素贝叶斯算法的健壮性比较好，对于不同类型的数据集不会呈现出太大的差异性。当数据集属性之间的关系相对比较独立时，朴素贝叶斯分类算法会有较好的效果。
缺点
- 属性独立性的条件同时也是朴素贝叶斯分类器的不足之处。数据集属性的独立性在很多情况下是很难满足的，因为数据集的属性之间往往都存在着相互关联，如果在分类过程中出现这种问题，会导致分类的效果大大降低。

11.4.8 总结

贝叶斯的计算

11.5 决策树

11.5.1认识决策树

(声明：本文内容来自机器学习实战和统计学习方法，是两者的整合，并非来自单个书籍）

决策树（decision tree）：是一种基本的分类与回归方法，此处主要讨论分类的决策树。

在分类问题中，表示基于特征对实例进行分类的过程，可以认为是if-then的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。

决策树通常有三个步骤：特征选择、决策树的生成、决策树的修剪。

用决策树分类：从根节点开始，对实例的某一特征进行测试，根据测试结果将实例分配到其子节点，此时每个子节点对应着该特征的一个取值，如此递归的对实例进行测试并分配，直到到达叶节点，最后将实例分到叶节点的类中。

下图为决策树示意图，圆点——内部节点，方框——叶节点

决策树学习的目标：根据给定的训练数据集构建一个决策树模型，使它能够对实例进行正确的分类。
决策树学习的本质：从训练集中归纳出一组分类规则，或者说是由训练数据集估计条件概率模型。
决策树学习的损失函数：正则化的极大似然函数
决策树学习的测试：最小化损失函数
决策树学习的目标：在损失函数的意义下，选择最优决策树的问题。
决策树原理和问答猜测结果游戏相似，根据一系列数据，然后给出游戏的答案。

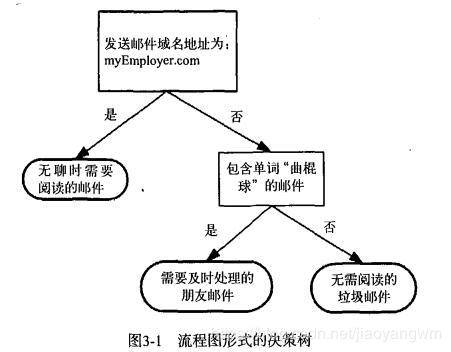
上图为一个决策树流程图，正方形代表判断模块，椭圆代表终止模块，表示已经得出结论，可以终止运行，左右箭头叫做分支。

上节介绍的k-近邻算法可以完成很多分类任务，但是其最大的缺点是无法给出数据的内在含义，决策树的优势在于数据形式非常容易理解

11.5.2 决策树分类原理

已知有四个特征值，推测是否贷款给某人。

先看房子、再看工作—>是否贷款？两个特征

年龄、信贷情况、工作看了三个特征

原理
- 信息熵
- 信息增益
1.信息熵
- 我们用信息熵来描述一个事件混乱程度的大小（一个事件我们一定知道结果，那么这个事件的混乱程度就是0；一个时间充满随机性，我们猜不到或者很难猜到结果，那么他的混乱度就很大）

假设：yes的概率为6/15，no的概率9/15

*H(总)= -（6/15*log6/15+9/15*log9/15)*=-0.971

+ 条件熵：
  + 条件1：yes的概率为2/5 no的概率3/5。
  + 条件2：yes的概率为3/5 no的概率2/5。
  + 条件3：yes的概率为4/5 no的概率1/5。

H(1)=-(2/5*log2/5+3/5*log3/5)

H(2)=-(3/5*log3/5+2/5*log2/5)

H(3)=-(4/5*log4/5+1/5*log1/5)

H(D|条件)=5/15H(1)+5/15H(2)+5/15H(3)

2.信息增益

在划分数据集之前之后信息发生的变化成为信息增益，知道如何计算信息增益，我们就可以计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。
g（D，条件）=H(总)-H(D|条件)

11.5.3 决策树API

from sklearn.tree import DecisionTreeClassifier
首先查看DecisionTreeClassifier都有哪些参数
DecisionTreeClassifier?
Init signature: 
DecisionTreeClassifier(
criterion='gini', 
splitter='best', 
max_depth=None, 
min_samples_split=2, 
min_samples_leaf=1, 
min_weight_fraction_leaf=0.0, 
max_features=None, 
random_state=None, 
max_leaf_nodes=None, 
min_impurity_decrease=0.0, 
min_impurity_split=None, 
class_weight=None, 
presort='deprecated', 
ccp_alpha=0.0)
						
重要参数：
criterion 为CART节点分割函数，默认为gini，当然也可以使用信息熵"entropy"
min_samples_split 分割节点所需的最小样本数
min_samples_leaf 每个叶子节点最小的样本数
min_impurity_decrease gini的分裂阈值，gini大于阈值继续分裂
ccp_alpha 裁剪阈值

11.5.4 案例:泰坦尼克号乘客生存预测

11.5.4.1 案例鸢尾花

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris

def tree_iris():
    """
    目的：决策树分析鸢尾花数据集
    1.导入数据集
    2.数据清理(标准数据集不需要这一步)
    3.分割数据
    4.特征工程
    5.决策树算法预估器流程
    6.模型调优
    7.模型评估
    :return:
    """
    iris = load_iris()
    x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,random_state=22)
    estimator=DecisionTreeClassifier(criterion="entropy")
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    estimator.fit(x_train,y_train)
    y_predict=estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("对比:\n", y_test == y_predict)
    score = estimator.score(x_test, y_test)  # 返回R的次方
    print('准确率为:\n', score)
    return None
if __name__ == '__main__':
    tree_iris()

11.5.4.2 案例泰坦尼克号

11.5.5 决策树可视化

sklearn.tree.expore_grahviz()该函数能够导出DOT格式
- tree.export_graphviz(estimator.out_file=“tree.dot”,feature_names=[’.’])

11.5.6 决策树总结

决策树的特点：

优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。
缺点：可能会产生过度匹配的问题
适用数据类型：数值型和标称型
优化：cart：剪枝
改进：随机森林

11.5.7 总结

信息值、信息增益的计算

DecisionTreeClassifier进项决策树的划分

可视化

11.6 随机森林

11.6.1 什么是集成学习方法

定义
- 在监督学习算法中，我们希望训练得到的模型是一个各方面都稳定表现良好的模型，但是实际情况中却往往得到的是在某方面有偏好的模型。集成学习则可以通过多个学习器相结合，来获得比单一学习器更优越的泛化性能。
- 集成学习是指通过构建并结合多个学习器来完成学习任务的分类系统，根据个体学习器是否为同一类可以分为同质集成和异质集成。
集成学习分类
- 目前根据个体学习器的生成方式，集成学习可以分为两大类：
  1）个体学习器之间存在较强的依赖性，必须串行生成的序列化方法：boosting类算法；
  2）个体学习器之间不存在强依赖关系，可以并行生成学习器：bagging和随机森林

11.6.2 什么是随机森林

随机森林中有许多的分类树。要将一个输入样本进行分类，需要将输入样本输入到每棵树中进行分类。每棵决策树都是一个分类器，那么对于一个输入样本，N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出

11.6.3 随机森林原理过程

训练集：目标值、特征值

随机：两个随机
- 训练集随机
- 特征随机
森林
- 包含多个决策树的分类群
为什么要随机抽样训练集？
- 如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的，这样的话完全没有bagging的必要；
为什么要有放回地抽样？
- 如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是”有偏的”，也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决，这种表决应该是”求同”，因此使用完全不同的训练集来训练每棵树这样对最终分类结果是没有帮助的，这样无异于是”盲人摸象”。

11.6.4 API

class sklearn.ensemble.RandomForestClassifier（
n_estimators ='warn'，
criterion =' gini '，
max_depth = None，
min_samples_split = 2，
min_samples_leaf = 1，min_weight_fraction_leaf = 0.0，max_features ='auto'，
max_leaf_nodes = None，min_impurity_decrease = 0.0，min_impurity_split =None，
bootstrap =True，
oob_score = False，
n_jobs = None，
random_state = None，
verbose = 0，
warm_start = False，
class_weight = None ）

n_estimators ：整数，可选（默认= 10）

森林里的树木数量。(120,200,300,500,800,1200)

*在版本0.20中更改：*默认值n_estimators将从版本0.20中的10更改为版本0.22中的100。

criterion ： string，optional（default =“gini”）

衡量分裂质量的功能。支持的标准是基尼杂质的“gini”和信息增益的“熵”。注意：此参数是特定于树的。

max_depth ：整数或无，可选（默认=无）

树的最大深度。如果为None，则扩展节点直到所有叶子都是纯的或直到所有叶子包含少于min_samples_split样本。

min_samples_split ： int，float，optional（default = 2）

拆分内部节点所需的最小样本数：

如果是int，则考虑min_samples_split为最小数量。
如果是浮点数，那么它min_samples_split是一个分数，是每个分割的最小样本数。ceil(min_samples_split * n_samples)

*更改版本0.18：*添加了分数的浮点值。

min_samples_leaf ： int，float，optional（default = 1）

叶节点所需的最小样本数。只有min_samples_leaf在每个左右分支中留下至少训练样本时，才会考虑任何深度的分裂点。这可能具有平滑模型的效果，尤其是在回归中。

如果是int，则考虑min_samples_leaf为最小数量。
如果是float，那么它min_samples_leaf是一个分数，是每个节点的最小样本数。ceil(min_samples_leaf * n_samples)

*更改版本0.18：*添加了分数的浮点值。

min_weight_fraction_leaf ： float，optional（默认= 0。）

需要在叶节点处的权重总和（所有输入样本的总和）的最小加权分数。当未提供sample_weight时，样本具有相同的权重。

max_features ： int，float，string或None，optional（default =“auto”）

寻找最佳分割时要考虑的功能数量：

如果是int，则考虑max_features每次拆分时的功能。
如果是浮点数，那么它max_features是一个分数，并且每次拆分时都会考虑特征。int(max_features * n_features)
如果是“自动”，那么max_features=sqrt(n_features)。
如果是“sqrt”，那么max_features=sqrt(n_features)（与“auto”相同）。
如果是“log2”，那么max_features=log2(n_features)。
如果没有，那么max_features=n_features。

注意：在找到节点样本的至少一个有效分区之前，搜索分割不会停止，即使它需要有效地检查多个max_features功能。

max_leaf_nodes ： int或None，可选（默认=无）

max_leaf_nodes以最好的方式种植树木。最佳节点定义为杂质的相对减少。如果为None则无限数量的叶节点。

min_impurity_decrease ： float，optional（默认= 0。）

如果该分裂导致杂质的减少大于或等于该值，则将分裂节点。

加权杂质减少方程式如下：

N_t  /  N  *  （杂质 -  N_t_R  /  N_t  *  right_impurity 
                    -  N_t_L  /  N_t  *  left_impurity ）

N样本总数在哪里，N_t是当前节点N_t_L的样本数，左子项中N_t_R的样本数，以及右子项中的样本数。

N，N_t，N_t_R并且N_t_L都指的是加权和，如果sample_weight获得通过。

版本0.19中的新功能。

min_impurity_split ： float，（默认值= 1e-7）

树木生长早期停止的门槛。如果节点的杂质高于阈值，节点将分裂，否则它是叶子。

从版本0.19min_impurity_split开始不推荐使用*：*已被弃用，支持 min_impurity_decrease0.19。默认值 min_impurity_split将在0.23中从1e-7变为0，并且将在0.25中删除。请min_impurity_decrease改用。

bootstrap ： boolean，optional（default = True）

是否在构建树时使用bootstrap样本。如果为False，则使用整个数据集构建每个树。

oob_score ： bool（默认= False）

是否使用袋外样品来估计泛化精度。

n_jobs ： int或None，可选（默认=无）

就业人数在两个并行运行fit和predict。 None除非在joblib.parallel_backend上下文中，否则表示1 。 -1表示使用所有处理器。有关详细信息，请参阅词汇表。

random_state ： int，RandomState实例或None，可选（默认=无）

如果是int，则random_state是随机数生成器使用的种子; 如果是RandomState实例，则random_state是随机数生成器; 如果为None，则随机数生成器是由其使用的RandomState实例np.random。

verbose ： int，optional（默认值= 0）

在拟合和预测时控制详细程度。

warm_start ： bool，optional（默认= False）

设置True为时，重用上一个调用的解决方案以适应并向整体添加更多估算器，否则，只需适合整个新林。请参阅词汇表。

class_weight ： dict，dicts 列表，“balanced”，“balanced_subsample”或None，可选（默认=无）

与表单中的类相关联的权重。如果没有给出，所有课程都应该有一个重量。对于多输出问题，可以按与y列相同的顺序提供dicts列表。{class_label: weight}

请注意，对于多输出（包括多标记），应为其自己的dict中的每个列的每个类定义权重。例如，对于四类多标签分类权重应为[{0：1,1：1}，{0：1,1：5}，{0：1,1：1}，{0：1,1： 1}]而不是[{1：1}，{2：5}，{3：1}，{4：1}]。

“平衡”模式使用y的值自动调整与输入数据中的类频率成反比的权重 n_samples / (n_classes * np.bincount(y))

“balanced_subsample”模式与“balanced”相同，只是基于每个生长的树的bootstrap样本计算权重。

对于多输出，y的每列的权重将相乘。

请注意，如果指定了sample_weight，这些权重将与sample_weight（通过fit方法传递）相乘。

11.6.5 随机森林预测案例

泰坦尼克衍生：

#%%

import graphviz
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.tree import DecisionTreeClassifier, export_graphviz
import pandas as pd
from sklearn.ensemble import RandomForestClassifier

"""
    目的：泰坦尼克号数据分析-决策树分析
    1.导入数据集
    2.数据清理(1.缺失值处理、2.特征值->字典类型)
    3.分割数据（特征值、目标值）
    4.特征工程(字典特征抽取)
    4+.随机森林
    5.决策树算法预估器流程
    6.模型调优
    7.模型评估
    :return:

"""

#%%

data=pd.read_csv('./data/titanic/titanic.csv')

#%%

data.head(0)

#%%

x=data[['row.names','pclass','age','sex']]
print(type(x))
y=data[['survived']]

#%% 缺失值处理

x['age'].fillna(x['age'].mean(),inplace=True)
x

#%% 转换字典

x=x.to_dict(orient='records')
x

#%%

x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=22)
type(y_train)

#%% 字典特征抽取

transfer = DictVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
#%% 随机森林
estimator=RandomForestClassifier()
# 网格搜索
param_dict={'n_estimators':[120,200,300,500,800,1200],'max_depth': [5,8,15,25,30]}
estimator=GridSearchCV(estimator,param_grid=param_dict,cv=3)
#%% 决策树

# estimator = DecisionTreeClassifier(criterion="entropy")
estimator.fit(x_train, y_train)
y_predict = estimator.predict(x_test)

#%%

print("y_predict:\n", y_predict)
# print('对比：\n',y_test==y_predict)
score = estimator.score(x_test, y_test)  # 返回R的次方
print('准确率为:\n', score)
print(estimator.best_params_)
print(estimator.best_score_)
print(estimator.best_estimator_)
print(estimator.cv_results_)
# export_graphviz(estimator, out_file='titanic_tree.dot',feature_names=transfer.get_feature_names())
# dot = graphviz.Digraph(comment='The Round Table')

11.6.6 总结

优点：

1）能够处理很高维度（feature很多）的数据，并且不用做特征选择（特征列采样）

2）训练完后，能够返回特征的重要性

3 ) 训练时树与树之间是相互独立的,易于并行化

4）可以处理缺失特征（决策树的优点）

缺点:

分裂的时候，偏向于选择取值较多的特征

12.回归与聚类算法

12.1 线性回归

12.1.1 线性回归原理

12.1.1.1 应用场景

房价预测
销售额度预测
金额：贷款额度预测、利用线性回归以及系数分析因子

12.1.1.2 定义

定义与公式
- 线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。
- y 为应变量 dependent variable
  x 为自变量 independent variable
  a 为斜率 coeffient
  b 为截距 intercept
  ε （读作epsilon）为误差，正态分布
  线性回归的目标是，找到一组a和b，使得ε最小

假设为因变量，为自变量，并且自变量与因变量之间为线性关系时，则多元线性回归模型为：
$W^Tx+b$
其中为因变量，为n个自变量，为个未知参数，为随机误差项。假设随机误差项为0时，因变量的期望值和自变量的线性方程为：

从下图来直观理解一下线性回归优化的目标——图中线段距离（平方）的平均值，也就是最小化到分割面的距离和。

12.1.1.3 线性回归的特征与目标的关系分析

线性关系

单特征与目标值的关系呈直线

双特征与目标值的关系呈平面

非线性关系

12.1.2 线性回归的损失与优化原理

线性回归的目标是，找到一组a和b，使得ε最小

真实关系：真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
随意假定：预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率
损失函数/cost/成本函数/目标函数：

目标：求每一个点到线的距离的和。最小二乘法。

12.1.3 方差 - 损失函数 Cost Function

在机器学习中，很多时候，我们需要找到一个损失函数。有了损失函数，我们就可以经过不断地迭代，找到损失函数的全局或者局部最小值（或者最大值）。损失函数使得我们的问题转化成数学问题，从而可以用计算机求解。在线性回归中，我们用方差作为损失函数。我们的目标是使得方差最小。

下面的表格解释了什么是方差。

其中SSE(Sum of Square Error)是总的方差，MSE（Mean Square Error）是方差的平均值。

而这里的损失函数，用的是0.5 * MSE。即：

$J(a,b)=\frac{1}{2n}\sum_{i=0}^{n}(y_i−\hat{y}_i )^2$

$记住，这里的损失函数是针对参数a和b的函数，y和\hat{y} 其实都是已知的。$

12.1.4 优化方法 Optimization Function

有了损失函数，我们还需要一个方法，使得我们可以找到这个损失函数的最小值。机器学习把他叫做优化方法。这里的优化方法，就是算损失的方向。或者说，当我的参数变化的时候，我的损失是变大了还是变小了。如果a变大了，损失变小了。那么，说明a增大这个方向是正确的，我们可以朝着这个方向继续小幅度的前进。反之，就应该考虑往相反的方向试试看。因为每个参数（a和b）都是一维的，所以，所谓的方向，无非就是正负符号。

12.2.2.1 正规方程

$w=(x^tx)^{-1}x^ty\\ 理解：x为特征值矩阵，y为目标值矩阵。$

12.2.2.2 梯度下降

这里，我们需要用偏微分的方法，得到损失函数的变化量。python还提供了sympy，你可以用sympy做微积分。即：
$KaTeX parse error: Can't use function '\(' in math mode at position 232: …n}(y_i-ax_i-b) \̲(̲-x_i)\\ = \frac…$

$KaTeX parse error: Can't use function '\(' in math mode at position 232: …n}(y_i-ax_i-b) \̲(̲-1)\\ = \frac{1…$

通过这个微积分迭代过程是小幅度进行的。这里，就需要一个超参数来控制这个过程。这个超参数就是α \alphaα，通常是0.01.

这时，我们就可以去更新a和b的值：
$a=a-α\frac{\partial J}{\partial a}\\ b=b-α\frac{\partial J}{\partial b}$
梯度下降和正规方程的对比：

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大可以使用	需要计算方程，时间复杂度高O(n3)

12.1.5 线性回归API

sklearn.linear_model.LinearRegression(fit_intercept=True) 通过正规方程优化 参数
fit_intercept：是否计算偏置 属性 LinearRegression.coef_：回归系数
LinearRegression.intercept_：偏置

sklearn.linear_model.SGDRegressor(loss=“squared_loss”,
fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。 参数： loss:损失类型
loss=”squared_loss”: 普通最小二乘法 fit_intercept：是否计算偏置 learning_rate :
string, optional 学习率填充 ‘constant’: eta = eta0 ‘optimal’: eta = 1.0 /
(alpha * (t + t0)) [default] ‘invscaling’: eta = eta0 / pow(t,
power_t) power_t=0.25:存在父类当中
对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。 
属性：
SGDRegressor.coef_：回归系数 
SGDRegressor.intercept_：偏置

12.1.6 回归性能评估

均方误差

sklearn.metrics.mean_squared_error

mean_squared_error(y_true, y_pred) 均方误差回归损失

 y_true:真实值

 y_pred:预测值 

return:浮点数结果

12.1.7 波士顿房价预测

获取数据集
划分数据集
特征工程
- 无量纲化
预估器流程
- fit()–>模型
- coef_intercept_
模型评估

from sklearn.datasets import load_boston  # 数据引入
from sklearn.model_selection import train_test_split  # 数据分割
from sklearn.preprocessing import StandardScaler  # 标准化
from sklearn.linear_model import LinearRegression  # 正规方程
from sklearn.linear_model import SGDRegressor  # 梯度下降法
from sklearn.metrics import mean_squared_error  # 均方误差
from sklearn.linear_model import Ridge  # 岭回归
import joblib  # 模型保存加载
import pandas as pd
import numpy as np


def regression_equation():
    """
    正规方程对波士顿房价进行预测
    :return:
    """
    #      获取数据集
    boston = load_boston()
    #     划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target)
    #     特征工程
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 预估器流程
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)
    y_predict=estimator.predict(x_test)
    print("正规方程权重系数为：\n", estimator.coef_)
    print("正规方程偏置为：\n", estimator.intercept_)

    # 模型评估
    print("预测值：\n",y_predict)
    error=mean_squared_error(y_test,y_predict)
    print("均方误差：\n",error)
    return None


def regression_equation2():
    """
    梯度下降对波士顿房价进行预测
    :return:
    """
    #      获取数据集
    boston = load_boston()
    print("特征数量：\n",boston.data.shape)
    #     划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target)
    #     特征工程
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 预估器流程
    estimator = SGDRegressor(eta0=0.001,max_iter=10000)
    estimator.fit(x_train, y_train)
    y_predict=estimator.predict(x_test)
    print("梯度下降权重系数为：\n", estimator.coef_)
    print("梯度下降偏置为：\n", estimator.intercept_)

    # 模型评估
    print("预测值：\n", y_predict)
    error=mean_squared_error(y_test,y_predict)
    print("均方误差：\n", error)
    return None


if __name__ == '__main__':
    regression_equation()
    regression_equation2()

12.2 欠拟合与过拟合

目标
- 说明线性回归（）的缺点
- 说明过拟合与欠拟合的原因及解决方法
应用
- 无

12.2.1 定义

拟合（Fitting）：就是说这个曲线能不能很好的描述某些样本，并且有比较好的泛化能力。

过拟合（Overfitting）：就是太过贴近于训练数据的特征了，在训练集上表现非常优秀，近乎完美的预测/区分了所有的数据，但是在新的测试集上却表现平平，不具泛化性，拿到新样本后没有办法去准确的判断。
欠拟合（UnderFitting）：测试样本的特性没有学到，或者是模型过于简单无法拟合或区分样本。

12.2.2 原因及解决方法

12.2.2.1解决过拟合的方法：

增大数据量，正则化（L1,L2），丢弃法Dropout（把其中的一些神经元去掉只用部分神经元去构建神经网络）

正则化
- L2正则化（常用）（权重衰减）
  - 作用：可以使得其中一些W的都很小，都接近于0
  - 优点：越小的参数说明模型越简单，越简单的模型越不容易产生拟合现象
  - ridge回归
  - 加入L2正则化后的损失数据
  - $J(w)=\frac{1}{2m}\sum_{i=0}^{m}(y_i−\hat{y}_i )^2+\lambda\sum_{j=1}^{n}w_j^2$
  - 损失函数加上惩罚项
- L1正则化
  - 作用：可以使其中一些W值直接为0
  - lasso回归

12.2.2.2解决欠拟合的方法：

优化模型，一般是模型过于简单无法描述样本的特性。

12.3 线性回归的改进-岭回归

岭回归，其实也是一种线性回归。只不过在算法建立回归方程时候，加上正则化的限制，从而达到解决过拟合的效果。

12.3.1 API


sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)
具有l2正则化的线性回归
alpha:正则化力度，也叫 λ
λ取值：0~1 1~10
solver:会根据数据自动选择优化方法
sag:如果数据集、特征都比较大，选择该随机梯度下降优化
normalize:数据是否进行标准化
normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
Ridge.coef_:回归权重
Ridge.intercept_:回归偏置

具有l2正则化的线性回归，可以进行交叉验证

12.3.2 对结果的影响

正则化力度越大，权重系数会越小
正则化力度越小，权重系数会越大

12.3.3 案例-波士顿房价

 regression_equation3():
    """
    岭回归，其实也是一种线性回归。只不过在算法建立回归方程时候，加上正则化的限制，从而达到解决过拟合的效果。
    :return:
    """
    #      获取数据集
    boston = load_boston()
    print("特征数量：\n",boston.data.shape)
    #     划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target)
    #     特征工程
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 预估器流程
    estimator = Ridge(alpha=0.5,max_iter=10000)
    estimator.fit(x_train, y_train)
    y_predict=estimator.predict(x_test)
    print("岭回归权重系数为：\n", estimator.coef_)
    print("岭回归偏置为：\n", estimator.intercept_)

    # 模型评估
    print("预测值：\n", y_predict)
    error=mean_squared_error(y_test,y_predict)
    print("均方误差：\n", error)
    return None

12.4 分类算法-逻辑回归与二分类

目标：
- 说明逻辑回归的损失函数
- 说明逻辑函数的优化方法
- 说明sigmold函数
- 知道逻辑回归的应用场景
- 知道精确率、召回率指标的区别
- 知道F1-score指标说明召回率的实际意义
- 说明如何解决样本不均衡情况下的评估
- 了解ROC曲线的意义说明AUC指标的大小
- 应用classification_report实现精确率、召回率计算
- 应用roc_auc_score实现指标计算

12.4.1 逻辑回归的应用场景

广告点击率是否会被点击
是否为垃圾邮件
是否患病
是否为金融诈骗
是否为虚假账号
正例 / 反例

12.4.2 逻辑回归的原理

1 输入
$h(w)=w_1x_1+w_2x_2+w_3x_3...+b$
2.激活数据

sigmoid函数

$g（\theta^Tx）=\frac{1}{1+e^{-\theta^Tx}}$

分析
- 回归的结果输入到sigmoid函数中
- 输出结果：[0,1]区间中的一个概率值，默认为0.5为阔值

logistic回归就是一个线性分类模型，它与线性回归的不同点在于：为了将线性回归输出的很大范围的数，例如从负无穷到正无穷，压缩到0和1之间，这样的输出值表达为“可能性”才能说服广大民众。当然了，把大值压缩到这个范围还有个很好的好处，就是可以消除特别冒尖的变量的影响（不知道理解的是否正确）。而实现这个伟大的功能其实就只需要平凡一举，也就是在输出加一个logistic函数。另外，对于二分类来说，可以简单的认为：**如果样本x属于正类的概率大于0.5，那么就判定它是正类，否则就是负类。**实际上，SVM的类概率就是样本到边界的距离，这个活实际上就让logistic regression给干了。
3.损失函数

逻辑回归的损失，称为对数似然损失，公式如下：

按类别分开：

当y=1时：即真实值为1，h(θ)得到的值为0时，从图中可以看出来，损失函数的值趋向于无穷，h(θ)得到的值为1时，损失函数的值趋向于0。

当y=0时：即真实值为0，h(θ)得到的值为1时，从图中可以看出来，损失函数的值趋向于无穷，h(θ)得到的值为0时，损失函数的值趋向于0。

综合完整损失函数，

计算损失：-（log(0.4)+(1-0)log(1-0.68)+log(0.41)+(1-0.55)log(1-0.55)+log(0.71)）
-log§：P值越大，损失越小。

4.优化损失

梯度下降法

Gradient descent 又叫 steepest descent，是利用一阶的梯度信息找到函数局部最优解的一种方法，也是机器学习里面最简单最常用的一种优化方法。它的思想很简单，和我开篇说的那样，要找最小值，我只需要每一步都往下走（也就是每一步都可以让代价函数小一点），然后不断的走，那肯定能走到最小值的地方，例如下图所示：

12.4.3 逻辑回顾API

sklearn.linear_model.LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)  
【solver是用什么样的梯度下降算法来解决】
solver可选参数:{'liblinear', 'sag', 'saga','newton-cg', 'lbfgs'}，
默认: 'liblinear'；用于优化问题的算法。
对于小数据集来说，“liblinear”是个不错的选择，而“sag”和'saga'对于大型数据集会更快。
对于多类问题，只有'newton-cg'， 'sag'， 'saga'和'lbfgs'可以处理多项损失;“liblinear”仅限于“one-versus-rest”分类。
penalty：正则化的种类  【选择什么样的正则化L1，L2】
C：正则化力度
C越大,惩罚越轻微,模型走向过拟合
C越小,惩罚越厉害,模型走向欠拟合
默认将类别数量少的当做
 LogisticRegression方法相当于SGDClassifier(loss=“log”,penalty=’ '),SGDClassifier实现了一个趋同的随机梯度下降学习，也支持平均随机梯度下降（ASGD），可以通过设置average=True。而使用LogisticRegression（实现了SAG）

12.4.4 案例癌症分类预算-良/恶性乳腺瘤预测

数据集下载：https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/

1.获取数据
- 读取的时候加上names
2.数据处理
- 处理缺失值
3.数据集划分
4.特征工程
- 无量纲化
逻辑回归预估器
模型评估

#%%
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

#%%


path="https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data"
column_name = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
               'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
               'Normal Nucleoli', 'Mitoses', 'Class']
data = pd.read_csv(path,names=column_name)
data.head()
#%% 处理”？“
data[data['Bare Nuclei']=="?"]=0
# data.to_csv("lo.csv")
#%% 筛选特征值和目标值
x=data.iloc[:,1:-1]
y=data["Class"]

#%% 划分数据集
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=22)
#%% 特征工程
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)
#%%
estimator=LogisticRegression()
estimator.fit(x_train,y_train)
y_prodict=estimator.predict(x_test)
#%%回归系数和偏执
estimator.coef_
#%%
estimator.intercept_
#%%模型评估
# 方法1
print("y_predict:\n",y_prodict)
print("直接对比真实值与预测值：\n",y_test)
# 方法二
score=estimator.score(x_test,y_test)
print("z准确率：\n",score)

12.4.5 分类的评估方法

精准率与召回率
- 混淆矩阵
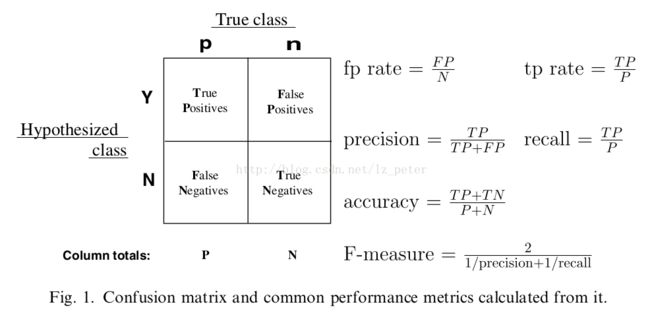
- 其中，
  
  TP：样本为正，预测结果为正；
  
  FP：样本为负，预测结果为正；
  
  TN：样本为负，预测结果为负；
  
  FN：样本为正，预测结果为负。
  
  准确率、精准率和召回率的计算公式如下：
  
  准确率（accuracy）： (TP + TN )/( TP + FP + TN + FN)
  
  精准率（precision）：TP / (TP + FP)，正确预测为正占全部预测为正的比例
  
  召回率（recall）： TP / (TP + FN)，正确预测为正占全部正样本的比例
  
  F-measure：precision和recall调和均值的2倍。
  
  观察上面的公式我们发现，精准率（precision）和召回率（recall）的分子都是预测正确的正类个数（即TP），区别在于分母。精准率的分母为预测为正的样本数，召回率的分母为原来样本中所有的正样本数。那么精准率和召回率的区别是什么呢，
API

由于模型无法完全正确预测数据。所以还需要衡量样本不均衡下的评估。

Roc曲线与AUC指标
- 了解TPR与FPR
- TPR=TP/（TP+FN）召回率
- FPR=FP/（FP+TN）
Roc曲线

ROC曲线的阈值问题

与前面的P-R曲线类似，ROC曲线也是通过遍历所有阈值来绘制整条曲线的。如果我们不断的遍历所有阈值，预测的正样本和负样本是在不断变化的，相应的在ROC曲线图中也会沿着曲线滑动。

如何判断ROC曲线的好坏？

改变阈值只是不断地改变预测的正负样本数，即TPR和FPR，但是曲线本身是不会变的。那么如何判断一个模型的ROC曲线是好的呢？这个还是要回归到我们的目的：FPR表示模型虚报的响应程度，而TPR表示模型预测响应的覆盖程度。我们所希望的当然是：虚报的越少越好，覆盖的越多越好。所以总结一下就是TPR越高，同时FPR越低（即ROC曲线越陡），那么模型的性能就越好。参考如下动态图进行理解。

ROC曲线无视样本不平衡

前面已经对ROC曲线为什么可以无视样本不平衡做了解释，下面我们用动态图的形式再次展示一下它是如何工作的。我们发现：无论红蓝色样本比例如何改变，ROC曲线都没有影响。

AUC（曲线下的面积）
为了计算 ROC 曲线上的点，我们可以使用不同的分类阈值多次评估逻辑回归模型，但这样做效率非常低。幸运的是，有一种基于排序的高效算法可以为我们提供此类信息，这种算法称为曲线下面积（Area Under Curve）。

比较有意思的是，如果我们连接对角线，它的面积正好是0.5。对角线的实际含义是：随机判断响应与不响应，正负样本覆盖率应该都是50%，表示随机效果。ROC曲线越陡越好，所以理想值就是1，一个正方形，而最差的随机判断都有0.5，所以一般AUC的值是介于0.5到1之间的。AUC的一般判断标准

**0.5 - 0.7：**效果较低，但用于预测股票已经很不错了

**0.7 - 0.85：**效果一般

**0.85 - 0.95：**效果很好

**0.95 - 1：**效果非常好，但一般不太可能

AUC计算的API

总结

auc只能用来评价二分类

auc非常适合评价样本不平衡的分类器性能

12.5 模型保存与加载

from sklearn.externals import joblib
保存：jolib.dump(model_name, ‘保存路径/model_name.pkl’)
加载：model_name= joblib.load(‘被保存的路径/model_name.pkl’)

eg:

def load_dump_demo():
    """
    模型保存和加载
    :return:
    """
    # 1.获取数据
    data = load_boston()

    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(岭回归)
    # # 4.1 模型训练
    # estimator = Ridge(alpha=1)
    # estimator.fit(x_train, y_train)
    #
    # # 4.2 模型保存
    # joblib.dump(estimator, "./data/test.pkl")

    # 4.3 模型加载
    estimator = joblib.load("./data/test.pkl")

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\n", y_predict)
    print("模型中的系数为:\n", estimator.coef_)
    print("模型中的偏置为:\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\n", error)

12.6 无监督学习K’聚类

12.6.1 什么是无监督学习

对象
与有监督学习不同的是，无监督学习所面向的数据是没有标签的。
那么如果给定一个无标签的数据集，怎么对其进行分类呢，这时就要使用聚类方法
K-means 就是聚类方法的一种
K-means 的流程：
k-means 是一个迭代算法，可以按以下步骤记忆

按照给定的K值产生K个不同的聚类中心
数据点与K个聚类中心进行距离上的计算，每个数据点选择其本身距离最近的聚类中心的类作为本轮的归属
按照新的数据分布，分别计算各类数据的均值来作为新的聚类中心
不断迭代2，3步骤，直到聚类中心不再进行变化算法结束
注意：如果分类的过程中发生某类簇中没有数据点的情况，就将那个簇删除掉；若对簇的数量有要求，就重新进行聚类中心的初始化。

失真函数
$J(c_1,c_2,\dots , c_m,\mu_1,\mu_2,\dots,\mu_k) = \frac{1}{m}\sum^{m}_{i=1}||x^{[i]} - \mu_{c^[i]} ||^2 \\ target: minJ(c,\mu)$
从数学角度来看，K-means算法是基于上式的损失函数来优化求解的。

$C_i 是第i个数据点的分类\\ μ_k 是聚类中心\\ μ_c[i] 代表的是某轮迭代时，数据点x的分类的聚类中心$

而K-means的两个迭代流程可以分别看作，失真函数J对于c和u做拉格朗日乘子法得到的最值解。
比如在簇分配时，就是固定u变量，计算所有x到u的距离，通过此方法来优化c
而在更新聚类中心时，就是固定c变量，并利用c来重新计算新的聚类中心。

聚类中心的初始化
在算法的第一步就是初始化聚类中心的位置，这里应用了一个较好的方法，就是在所有的数据点里随机化选择k个（不放回抽取）点作为初始的聚类中心，依据此来开始算法的迭代

但是这种随机化分配的变化性较强，就使得聚类的结果会出现问题，产生局部最优解

此时对应的解决办法就是，多次（比如100次）随机化初始聚类中心，然后进行聚类的分配，并计算每次最终的分类对应的失真函数的值，选择最小的一次作为最终的分类结果。这种方法对K在2到10之间的聚类问题很有效果，当类的数量太多的时候，这种方法的作用就不会那么明显了。

K的选择
通常来讲，K的选择是经过人的思考或经验决定的，它通常取决于要解决的问题或要达到的目的，因此并不存在一种自动的最优的k的选择方法
若不知道K应该取多少，可以通过”肘部法则“来进行尝试，但往往并不会取得太好的效果。

12.6.2 无监督学习包含算法

聚类
- K-means(k均值聚类)
降维
- PCA

12.6.3 K-means原理

1.（随机）选择K个聚类的初始中心；

2.对任意一个样本点，求其到K个聚类中心的距离，将样本点归类到距离最小的中心的聚类，如此迭代n次；

3.每次迭代过程中，利用均值等方法更新各个聚类的中心点(质心)；

4.对K个聚类中心，利用2,3步迭代更新后，如果位置点变化很小(可以设置阈值)，则认为达到稳定状态，迭代结束，对不同的聚类块和聚类中心可选择不同的颜色标注。

12.6.4 k-means API

class sklearn.cluster.KMeans(
    n_clusters=8, 
    init=’kmeans++’, 
    n_init=10, 
    max_iter=300, 
    tol=0.0001, 
    precompute_distances=’auto’, 
    verbose=0, 
    random_state=None, 
    copy_x=True, 
    n_jobs=None, 
    algorithm=’auto’)

n_clusters：整型，缺省值=8 【生成的聚类数，即产生的质心（centroids）数。】 
max_iter：整型，缺省值=300 
执行一次k-means算法所进行的最大迭代数。 
n_init：整型，缺省值=10 
用不同的质心初始化值运行算法的次数，最终解是在inertia意义下选出的最优结果。 
init：有三个可选值：’k-means++’， ‘random’，或者传递一个ndarray向量。 
此参数指定初始化方法，默认值为 ‘k-means++’。 
（１）‘k-means++’ 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛（即上文中的k-means++介绍） 
（２）‘random’ 随机从训练数据中选取初始质心。 
（３）如果传递的是一个ndarray，则应该形如 (n_clusters, n_features) 并给出初始质心。 
precompute_distances：三个可选值，‘auto’，True 或者 False。 
预计算距离，计算速度更快但占用更多内存。 
（１）‘auto’：如果 样本数乘以聚类数大于 12million 的话则不预计算距离。This corresponds to about 100MB overhead per job using double precision. 
（２）True：总是预先计算距离。 
（３）False：永远不预先计算距离。 
tol：float型，默认值= 1e-4　与inertia结合来确定收敛条件。 
n_jobs：整型数。　指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。 
（１）若值为 -1，则用所有的CPU进行运算。若值为1，则不进行并行运算，这样的话方便调试。 
（２）若值小于-1，则用到的CPU数为(n_cpus + 1 + n_jobs)。因此如果 n_jobs值为-2，则用到的CPU数为总CPU数减1。 
random_state：整型或 numpy.RandomState 类型，可选 
用于初始化质心的生成器（generator）。如果值为一个整数，则确定一个seed。此参数默认值为numpy的随机数生成器。 
copy_x：布尔型，默认值=True 
当我们precomputing distances时，将数据中心化会得到更准确的结果。如果把此参数值设为True，则原始数据不会被改变。如果是False，则会直接在原始数据 上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算，所以数据返回后，原始数据和计算前可能会有细小差别。

verbose ： int，默认值为0

详细模式。

algorithm ： “auto”，“full”或“elkan”，默认=“auto”

12.6.5 案例k-means对instacart market用户聚类

1.导入数据

2.数据清理

3.特征工程

4.预估器流程

5.看结果

6.模型评估

12.6.6 K性能评估指标

轮廓系数
$SC_i=\frac{b_i-a_i}{max(b_ia_i)}\\ a_i内部距离 b_i外部距离$
判断依据：高内聚、低耦合

外部距离最大化、内部距离最小化

取值[-1,1]效果由低到高

API

sklearn.metrics.silhouette_score(x,labels)

x,特征值

labels 被聚类的目标值

13.6.7 k聚类总结

优点
1）原理比较简单，实现也是很容易，收敛速度快。
2）聚类效果较优。
3）算法的可解释度比较强。
4）主要需要调参的参数仅仅是簇数k。

缺点
1）K值的选取不好把握
2）对于不是凸的数据集比较难收敛
3）如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳。
4）最终结果和初始点的选择有关，容易陷入局部最优。
5）对噪音和异常点比较的敏感。

应用场景：

1.没有目标值

2.聚类一般作在分类前面

13.7 总结

机器学习算法一般是这样一个步骤：

1）对于一个问题，我们用数学语言来描述它，然后建立一个模型，例如回归模型或者分类模型等来描述这个问题；

2）通过最大似然、最大后验概率或者最小化分类误差等等建立模型的代价函数，也就是一个最优化问题。找到最优化问题的解，也就是能拟合我们的数据的最好的模型参数；

3）然后我们需要求解这个代价函数，找到最优解。这求解也就分很多种情况了。

[1] csdn机器学习众多的相关博主（很多嘻嘻嘻）

.对K个聚类中心，利用2,3步迭代更新后，如果位置点变化很小(可以设置阈值)，则认为达到稳定状态，迭代结束，对不同的聚类块和聚类中心可选择不同的颜色标注。

12.6.4 k-means API

class sklearn.cluster.KMeans(
    n_clusters=8, 
    init=’kmeans++’, 
    n_init=10, 
    max_iter=300, 
    tol=0.0001, 
    precompute_distances=’auto’, 
    verbose=0, 
    random_state=None, 
    copy_x=True, 
    n_jobs=None, 
    algorithm=’auto’)

n_clusters：整型，缺省值=8 【生成的聚类数，即产生的质心（centroids）数。】 
max_iter：整型，缺省值=300 
执行一次k-means算法所进行的最大迭代数。 
n_init：整型，缺省值=10 
用不同的质心初始化值运行算法的次数，最终解是在inertia意义下选出的最优结果。 
init：有三个可选值：’k-means++’， ‘random’，或者传递一个ndarray向量。 
此参数指定初始化方法，默认值为 ‘k-means++’。 
（１）‘k-means++’ 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛（即上文中的k-means++介绍） 
（２）‘random’ 随机从训练数据中选取初始质心。 
（３）如果传递的是一个ndarray，则应该形如 (n_clusters, n_features) 并给出初始质心。 
precompute_distances：三个可选值，‘auto’，True 或者 False。 
预计算距离，计算速度更快但占用更多内存。 
（１）‘auto’：如果 样本数乘以聚类数大于 12million 的话则不预计算距离。This corresponds to about 100MB overhead per job using double precision. 
（２）True：总是预先计算距离。 
（３）False：永远不预先计算距离。 
tol：float型，默认值= 1e-4　与inertia结合来确定收敛条件。 
n_jobs：整型数。　指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。 
（１）若值为 -1，则用所有的CPU进行运算。若值为1，则不进行并行运算，这样的话方便调试。 
（２）若值小于-1，则用到的CPU数为(n_cpus + 1 + n_jobs)。因此如果 n_jobs值为-2，则用到的CPU数为总CPU数减1。 
random_state：整型或 numpy.RandomState 类型，可选 
用于初始化质心的生成器（generator）。如果值为一个整数，则确定一个seed。此参数默认值为numpy的随机数生成器。 
copy_x：布尔型，默认值=True 
当我们precomputing distances时，将数据中心化会得到更准确的结果。如果把此参数值设为True，则原始数据不会被改变。如果是False，则会直接在原始数据 上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算，所以数据返回后，原始数据和计算前可能会有细小差别。

verbose ： int，默认值为0

详细模式。

algorithm ： “auto”，“full”或“elkan”，默认=“auto”

12.6.5 案例k-means对instacart market用户聚类

1.导入数据

2.数据清理

3.特征工程

4.预估器流程

5.看结果

6.模型评估

12.6.6 K性能评估指标

轮廓系数
$SC_i=\frac{b_i-a_i}{max(b_ia_i)}\\ a_i内部距离 b_i外部距离$
判断依据：高内聚、低耦合

外部距离最大化、内部距离最小化

取值[-1,1]效果由低到高

API

sklearn.metrics.silhouette_score(x,labels)

x,特征值

labels 被聚类的目标值

13.6.7 k聚类总结

优点
1）原理比较简单，实现也是很容易，收敛速度快。
2）聚类效果较优。
3）算法的可解释度比较强。
4）主要需要调参的参数仅仅是簇数k。

应用场景：

1.没有目标值

2.聚类一般作在分类前面

13.7 总结

机器学习算法一般是这样一个步骤：

1）对于一个问题，我们用数学语言来描述它，然后建立一个模型，例如回归模型或者分类模型等来描述这个问题；

3）然后我们需要求解这个代价函数，找到最优解。这求解也就分很多种情况了。

[1] csdn机器学习众多的相关博主（嘻嘻嘻）

机器学习从零到一的基础知识总集篇

文章目录

1. 定义

2. 机器学习原理

3. 机器学习的分类

3.1 基于学习策略的分类

3.2 基于学习方法的分类

3.3 基于学习方式的分类

3.4 基于数据形式的分类

3.5 基于学习目标的分类

4. 常见算法

4.1 决策树算法

4.2 朴素贝叶斯算法

4.3 支持向量机算法

4.4 随机森林算法

4.5 人工神经网络算法

4.6 Boosting与Bagging算法

4.7 关联规则算法

4.8 EM（期望最大化）算法

4.9 深度学习

5. 应用

5.1 数据分析与挖掘

5.2 模式识别

5.3 在生物信息学上的应用

5.4 更广阔的领域

5.5 具体应用

6. 数据学习开发流程

7. 学习目标

8. 数据集

8.1 数据集

8.1.1 可用数据集

9. Python数据分析工具介绍

9.1 Scikit-learn工具介绍

9.3 Scikit-learn数据集api介绍

9.4 数据集的划分

10.特征工程

10.1 定义

10.2 模块流程

10.2.1 特征抽取

10.2.1.1字典特征提取

10.2.1.1文本特征提取

10.2.2 特征预处理

10.2.2.1.归一化（方法不止这一种）

10.2.2.1.标准化

10.2.3 特征降维

10.2.3.1 特征选择

10.2.3.2 主成分分析（PCA）

案例分析

1. insta_cart市场篮子分析

11. 分类算法

11.1 sklearn的转换器和预估器

11.1.1转换器

11.1.2预估器

11.2 KNN算法

11.2.1 什么是KNN算法

11.2.2 KNN算法API

11.2.3 案例：莺尾花种类预测

11.2.4 KNN算法总结

优点：KNN方法思路简单，易于理解，易于实现，无需估计参数

11.3 模型选择与调优

11.3.1 什么是交叉验证

11.3.2 超参数搜索-网格搜索

11.3.3 鸢尾花案例加k值调优

11.3.4 预测fecebook签到

11.3.5 总结

11.4 朴素贝叶斯算法

11.4.1 定义

11.4.2 概率基础

11.4.3 联合概率、条件概率、与相互独立

11.4.4 贝叶斯公式

11.4.6 案例：20类新闻分类

11.4.7 朴素贝叶斯算法总结

11.4.8 总结

11.5 决策树

11.5.1认识决策树

11.5.2 决策树分类原理

11.5.3 决策树API

11.5.4 案例:泰坦尼克号乘客生存预测

11.5.4.1 案例鸢尾花

11.5.4.2 案例泰坦尼克号