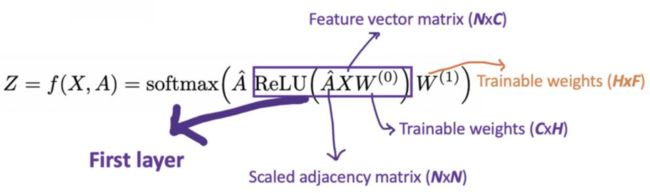
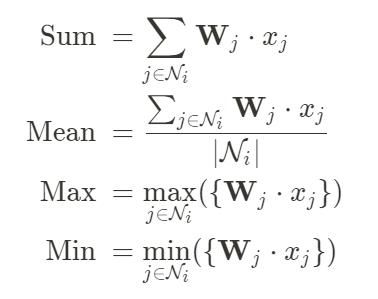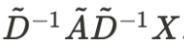图神经网络基础

1.图神经网络应用分析

         

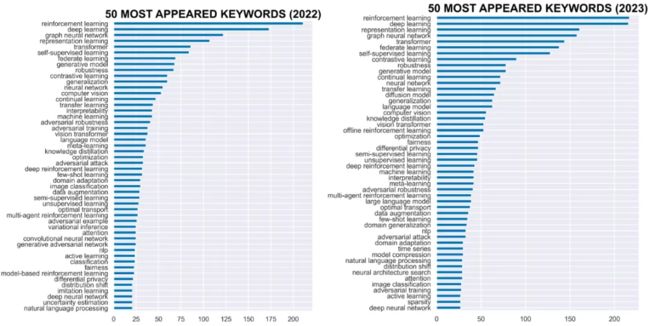
        从深度学习顶会ICLR投稿主题来看，2022年和2023年强化学习、深度学习、表征学习、图神经网络等都是最热门的方向。

应用领域

 芯片设计

         将芯片的每一个单元的联通看成一个图，实现AI设计芯片

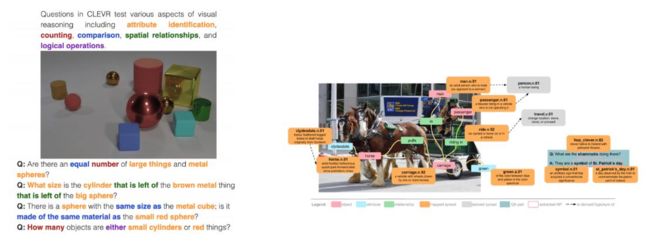
场景分析与问题推理

       结构化的数据的特征可能并不是独立的，而是具有关系。通过点和边可以组成一个个关系图。比如说警察破案

推荐系统 

         推荐系统本质上来说可以看做一个关系图，点和点之间肯定存在着关系

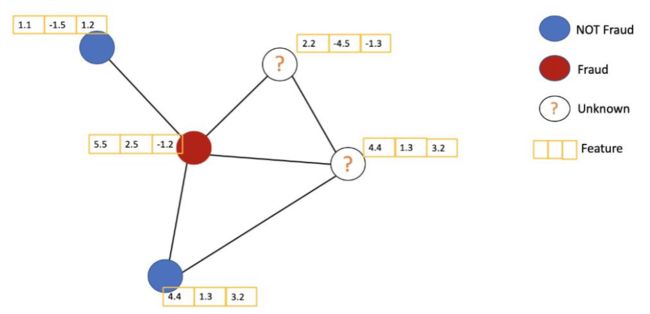
 欺诈检测，风控相关

        对个人信息进行测评，从而将贷款用户加入到图模型中，构建出用户和海量用户的关系，从而进行风险评估。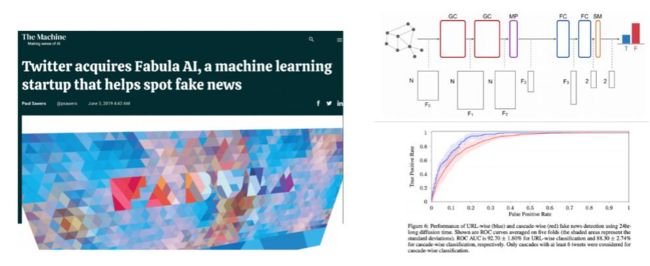 

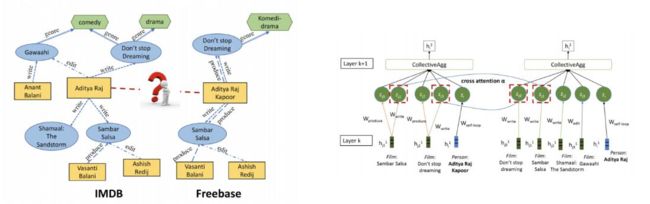
 知识图谱

        知识图谱，现在最大的应用是做智能客服，知识图谱也可以看做是一个关系图

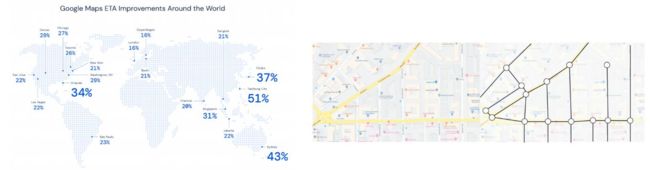
道路交通，动态流量预测 

        比如说做动态的红绿灯调整。根据人流量、车流量动态调整红绿灯。但是，一个十字路口红绿灯的改变肯定会影响到其他红绿灯。 

自动驾驶，无人机等场景 

        比如自动驾驶领域的激光雷达，扫描的各个物体肯定也是存在一定的关系的。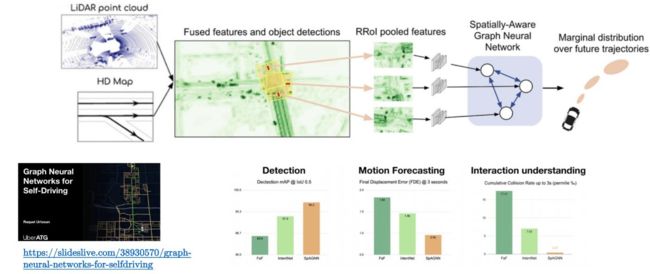 

化学，医疗等场景等 

        科学家做的实验是有限的，而计算机可以快速的大量的对比分析实验。

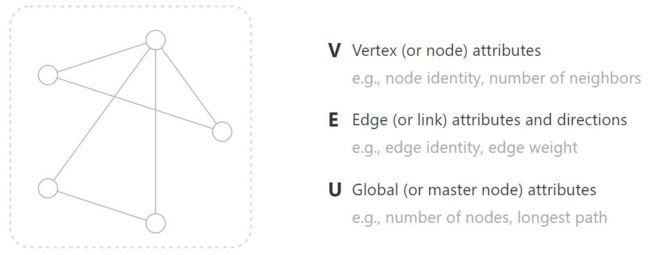
图的基本组成 

• 点:与自己的定义有关，一般来说，我们将特征向量看成点
• 边:也是一个向量，代表了点和点的关系
•  图:全局特征表示，比如说：最简单的方法，将所有的点进行加权平均     

        对于不同的任务，我们有针对与点去做，也有针对与边去做，还有针对于整个图去做。

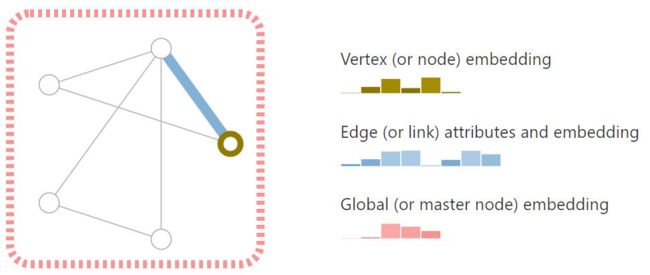
        从本质来说，图神经网络也是在做特征提取，整合特征，类似于word2vec利用词与词之间的关系去学习词向量。图神经网络也是利用点于点的关系去重构点和边的向量表示，进而重构整个图的特征。 

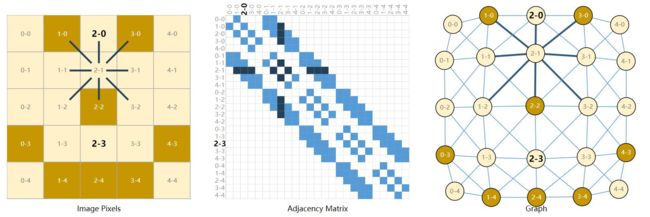
图的邻接矩阵 

        以图像为例子，假如说我们认为，一个点跟他相邻的8个点有关系，但是这件事怎么让计算机知道呢？因此我们定义一个领接矩阵表示点与点之间的关系。需要注意的是，假如图像大小为H,W。那么邻接矩阵 的size应该为HW*HW，表示每一个像素点与其他像素点的关系。

         

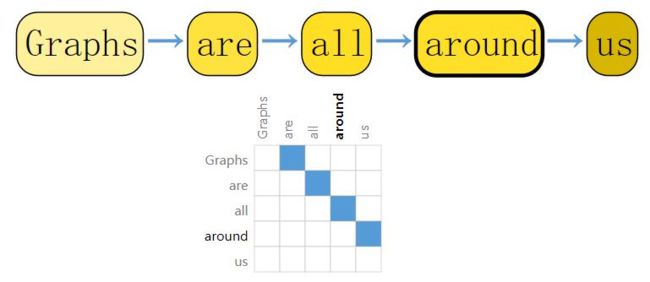
文本数据也可以表示图的形式，邻接矩阵表示的连接关系 

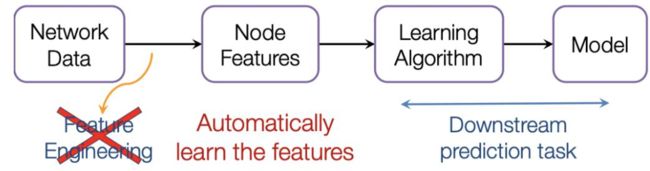
应用范围 

                为什么我们一般不在图像和文本中使用图神经网络呢？那是因为我们的图像和文本的输入都很固定，对于图像我们可以resize成固定大小 ，对于文本我们可以固定长度和词向量大小。不需要特殊的邻接矩阵。

        因此，图神经网络的优势主要为非结构化的数据，比如分子结构、社交网络等等。

邻接矩阵

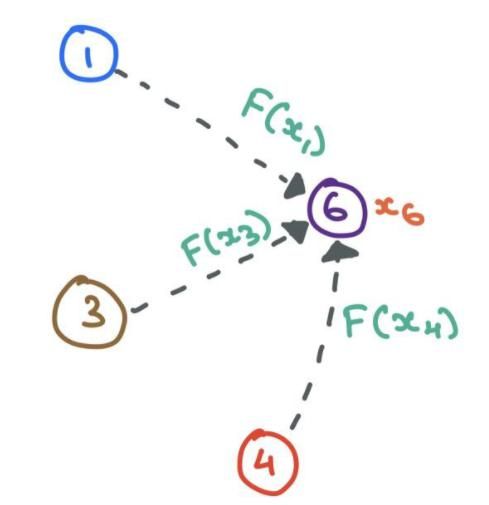
        一般邻接矩阵表达形式如下，并不是一个N*N的矩阵，因为这样表示的话矩阵大而稀疏，而是保存source,target ，表示由谁到谁。 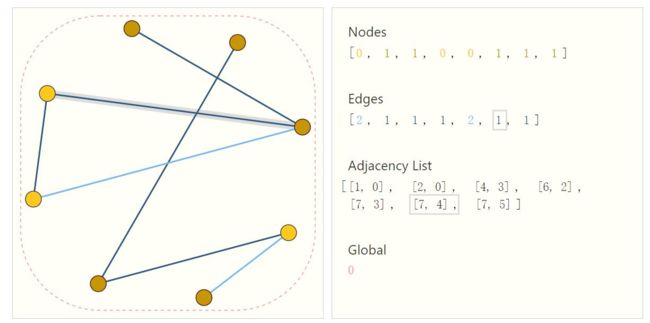      每个点的特征该如何更新呢？ 

         我们可以为每个边训练一个权重，聚合操作可以当作全连接层，但是更新的方法有很多，可以自己设置

   

 多层GNN的作用

        GNN的本质就是更新各部分特征，其中输入是特征，输出也是特征，邻接矩阵也不会变的。但是，经过一层GNN的更新后，每个点的特征受到了该点邻居的直接影响。在第二层GNN中，我们是使用更新后的特征进行更新，不仅能够受到邻居的直接影响，还能传递邻居的邻居的间接影响。

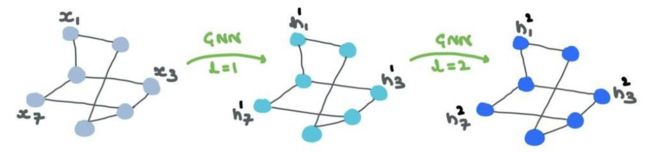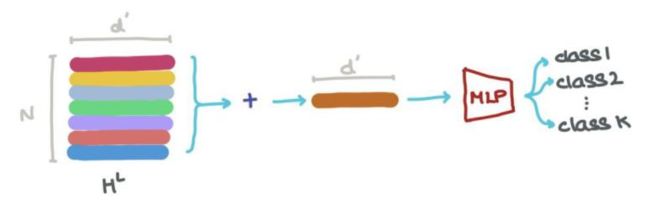
 特征提取后的输出:

        各个点特征组合，可以图分类：

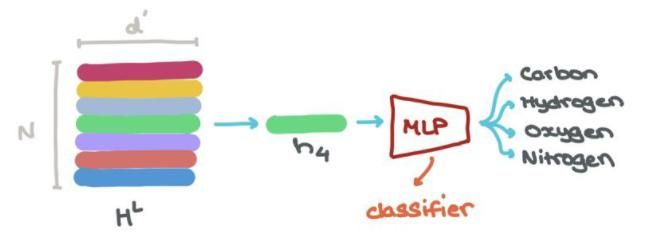
        各个节点也可以分类： 

        边也是如此：

图卷积模型GCN 

        图卷积和卷积具有根本上的图，图卷积是根据图来做的，处理的数据也是一些非结构化的数据，

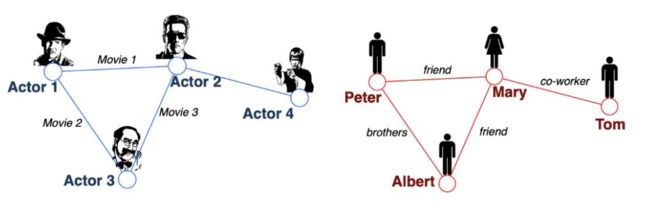常见任务 

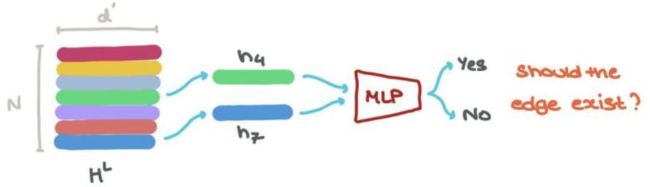
        节点分类，对每个节点进行预测，不同点是否有连接预测

        整个图分类，部分图分类等，不同子图是否相似，异常检测等

        GCN归根到底还是要完成特征提取操作，只不过输入对象不是固定格式

         

如何获取特征呢？ 

        处理方式还是和神经网络一样，通常交给GCN两个东西就行：1.各节点输入特征；2.网络结构图

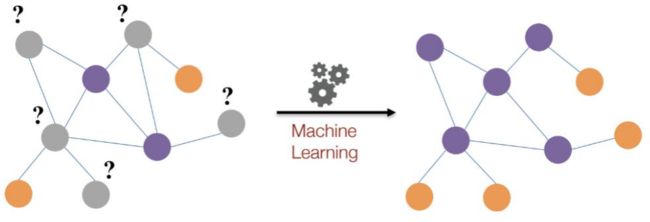
Semi-supervised learning 

        这个也是GCN优势，不需要全部标签，用少量标签也能训练，计算损失时只用有标签的

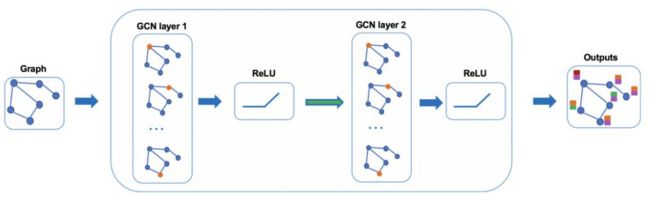
GCN的基本思想 

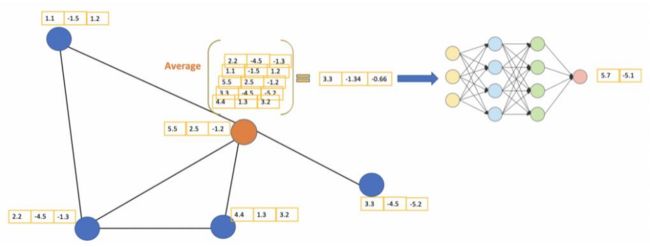
        针对橙色节点，计算它的特征：平均其邻居特征(包括自身)后传入神经网络

网络层数         

        GCN也可以做多层，每一层输入的还是节点特征，然后将当前特征与网络结构图继续传入下层就可以不断算下去了

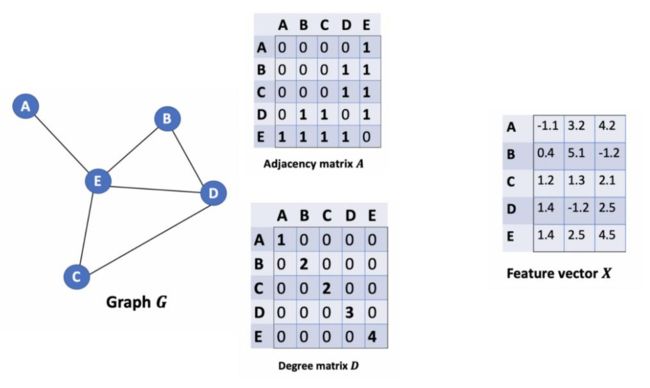
图的基本组成 

G是整个图

A是邻接矩阵

D是各个节点的度，表示与几个节点相连

F是每个节点的特征

特征计算方法        

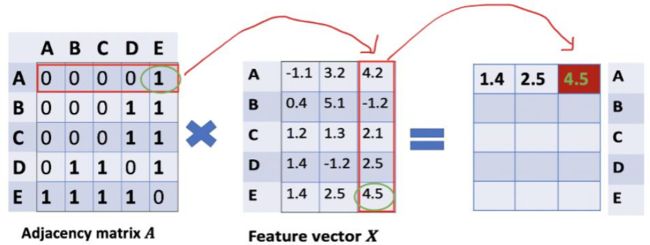
        其实就是邻接矩阵与特征矩阵进行乘法操作，表示聚合邻居信息

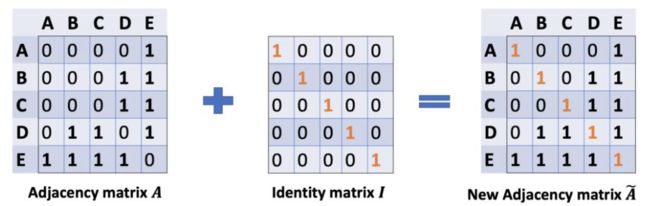
        但是，上面的做法只考虑了邻居的特征，没有考虑自己的特征，因此，我们将邻接矩阵对角线置1，表示在邻接矩阵加上自己的信息。同时相应的度也有加1.

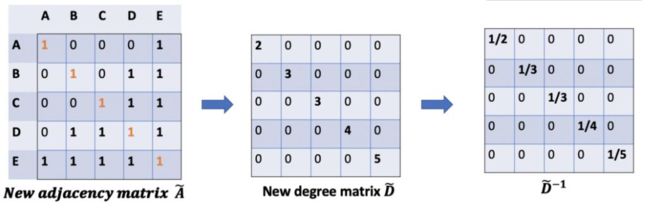
        但是还有一个问题，这样的计算结果会使邻居越多的值越大，这怎么解决呢？我们构建了一个度矩阵，我们乘以就相当于做了归一化操作了。

        

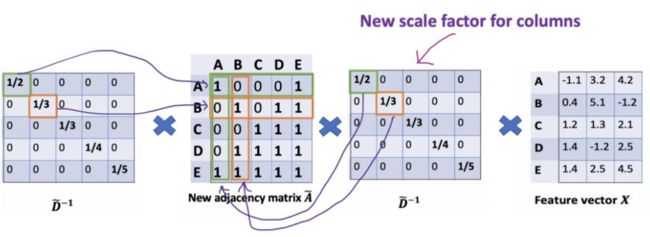
        目前公式为： 即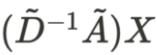，左乘的最终结果会作用到每一行上，相当于对行做了归一化，但是没有对列考虑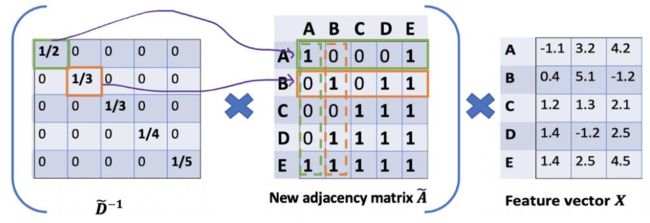

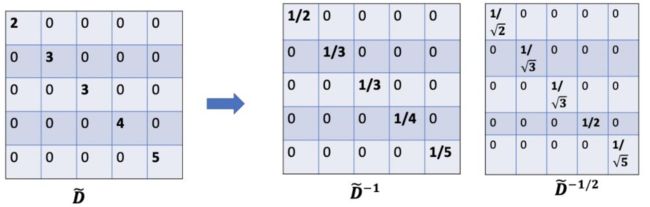
         因此，我们右乘相当于对列做了归一化

 但是，这样对行列进行归一化让特征值太小了。因此，行列进行归一化首先取根号。即

 个人理解:

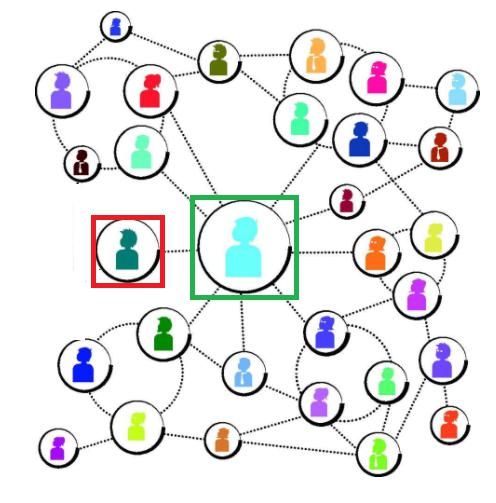
        比如说图中的小绿和小蓝，小绿只与小蓝有关系，度为1，而小蓝与多个节点都有关系，度很大，小绿对小蓝的影响有限。假如我们只对行进行归一化（即只对小绿的度进行归一化），那么就很可能认为小绿与小蓝极为相似，实际上小蓝受到很多节点的影响与小绿的关系不是特别紧密。因此，在归一化时，不仅用小绿本身的度，还用小蓝的度进行归一化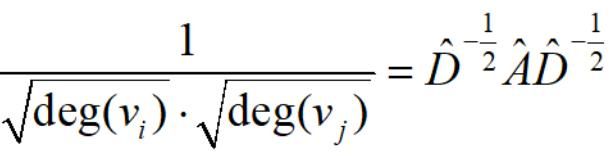， ，将其权重参数变小。

         

 基本公式

        代表归一化的邻接矩阵，表示对特征进行整合，RELU是非线性激活，W表示一组神经网络