bp神经网络 损失函数,bp神经网络参数优化

BP神经网络在线学习的误差计算方法

标准BP算法中，每输入一个样本，都要回传误差并调整权值，这种对每个样本轮训的方法称为“单样本训练”。

由于单样本训练遵循的是只顾眼前的“本位主义”原则，只针对每个样本产生的误差进行调整，难免顾此失彼，使训练次数增加，导致收敛速度过慢。

因此，有另外一种方法，就是在所有样本输入之后，计算网络的总误差，再根据总误差调整权值，这种累积误差的批处理方式称为“批训练”或“周期训练”。在样本数较多时，批训练比单样本训练的收敛速度更快。

BP人工神经网络方法

（一）方法原理人工神经网络是由大量的类似人脑神经元的简单处理单元广泛地相互连接而成的复杂的网络系统rbsci。理论和实践表明，在信息处理方面，神经网络方法比传统模式识别方法更具有优势。

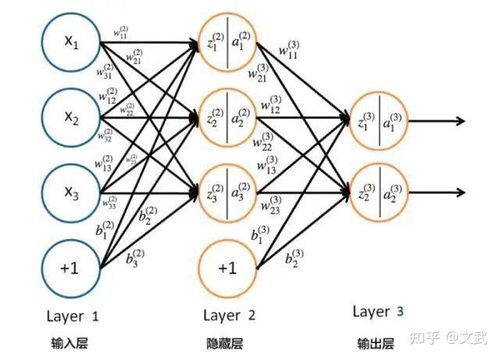
人工神经元是神经网络的基本处理单元，其接收的信息为x1，x2，…，xn，而ωij表示第i个神经元到第j个神经元的连接强度或称权重。

神经元的输入是接收信息X＝（x1，x2，…，xn）与权重W＝｛ωij｝的点积，将输入与设定的某一阈值作比较，再经过某种神经元激活函数f的作用，便得到该神经元的输出Oi。

常见的激活函数为Sigmoid型。

人工神经元的输入与输出的关系为地球物理勘探概论式中：xi为第i个输入元素，即n维输入矢量X的第i个分量；ωi为第i个输入与处理单元间的互联权重；θ为处理单元的内部阈值；y为处理单元的输出。

常用的人工神经网络是BP网络，它由输入层、隐含层和输出层三部分组成。BP算法是一种有监督的模式识别方法，包括学习和识别两部分，其中学习过程又可分为正向传播和反向传播两部分。

正向传播开始时，对所有的连接权值置随机数作为初值，选取模式集的任一模式作为输入，转向隐含层处理，并在输出层得到该模式对应的输出值。每一层神经元状态只影响下一层神经元状态。

此时，输出值一般与期望值存在较大的误差，需要通过误差反向传递过程，计算模式的各层神经元权值的变化量。这个过程不断重复，直至完成对该模式集所有模式的计算，产生这一轮训练值的变化量Δωij。

在修正网络中各种神经元的权值后，网络重新按照正向传播方式得到输出。实际输出值与期望值之间的误差可以导致新一轮的权值修正。正向传播与反向传播过程循环往复，直到网络收敛，得到网络收敛后的互联权值和阈值。

（二）BP神经网络计算步骤（1）初始化连接权值和阈值为一小的随机值，即W（0）＝任意值，θ（0）＝任意值。（2）输入一个样本X。

（3）正向传播，计算实际输出，即根据输入样本值、互联权值和阈值，计算样本的实际输出。

其中输入层的输出等于输入样本值，隐含层和输出层的输入为地球物理勘探概论输出为地球物理勘探概论式中：f为阈值逻辑函数，一般取Sigmoid函数，即地球物理勘探概论式中：θj表示阈值或偏置；θ0的作用是调节Sigmoid函数的形状。

较小的θ0将使Sigmoid函数逼近于阈值逻辑单元的特征，较大的θ0将导致Sigmoid函数变平缓，一般取θ0＝1。

（4）计算实际输出与理想输出的误差地球物理勘探概论式中：tpk为理想输出；Opk为实际输出；p为样本号；k为输出节点号。

（5）误差反向传播，修改权值地球物理勘探概论式中：地球物理勘探概论地球物理勘探概论（6）判断收敛。若误差小于给定值，则结束，否则转向步骤（2）。

（三）塔北雅克拉地区BP神经网络预测实例以塔北雅克拉地区S4井为已知样本，取氧化还原电位，放射性元素Rn、Th、Tc、U、K和地震反射构造面等7个特征为识别的依据。

构造面反映了局部构造的起伏变化，其局部隆起部位应是油气运移和富集的有利部位，它可以作为判断含油气性的诸种因素之一。

在该地区投入了高精度重磁、土壤微磁、频谱激电等多种方法，一些参数未入选为判别的特征参数，是因为某些参数是相关的。

在使用神经网络方法判别之前，还采用K-L变换（Karhaem-Loeve）来分析和提取特征。S4井位于测区西南部5线25点，是区内唯一已知井。

该井在5390.6m的侏罗系地层获得40.6m厚的油气层，在5482m深的震旦系地层中获58m厚的油气层。

取S4井周围9个点，即4～6线的23～25点作为已知油气的训练样本；由于区内没有未见油的钻井，只好根据地质资料分析，选取14～16线的55～57点作为非油气的训练样本。

BP网络学习迭代17174次，总误差为0.0001，学习效果相当满意。以学习后的网络进行识别，得出结果如图6-2-4所示。

图6-2-4塔北雅克拉地区BP神经网络聚类结果（据刘天佑等，1997）由图6-2-4可见，由预测值大于0.9可得5个大封闭圈远景区，其中测区南部①号远景区对应着已知油井S4井；②、③号油气远景区位于地震勘探所查明的托库1、2号构造，该两个构造位于沙雅隆起的东段，其西段即为1984年钻遇高产油气流的Sch2井，应是含油气性好的远景区；④、⑤号远景区位于大涝坝构造，是yh油田的组成部分。

BP神经网络(误差反传网络)

虽然每个人工神经元很简单，但是只要把多个人工神经元按一定方式连接起来就构成了一个能处理复杂信息的神经网络。采用BP算法的多层前馈网络是目前应用最广泛的神经网络，称之为BP神经网络。

它的最大功能就是能映射复杂的非线性函数关系。

对于已知的模型空间和数据空间，我们知道某个模型和他对应的数据，但是无法写出它们之间的函数关系式，但是如果有大量的一一对应的模型和数据样本集合，利用BP神经网络可以模拟(映射)它们之间的函数关系。

一个三层BP网络如图8.11所示，分为输入层、隐层、输出层。它是最常用的BP网络。理论分析证明三层网络已经能够表达任意复杂的连续函数关系了。只有在映射不连续函数时(如锯齿波)才需要两个隐层[8]。

图8.11中，X=(x1，…，xi，…，xn)T为输入向量，如加入x0=-1，可以为隐层神经元引入阀值;隐层输出向量为:Y=(y1，…，yi，…，ym)T，如加入y0=-1，可以为输出层神经元引入阀值;输出层输出向量为:O=(o1，…，oi，…，ol)T;输入层到隐层之间的权值矩阵用V表示，V=(V1，…，Vj，…，Vl)T，其中列向量Vj表示隐层第j个神经元的权值向量;隐层到输出层之间的权值矩阵用W表示，W=(W1，…，Wk，…，Wl)T，其中列向量Wk表示输出层第k个神经元的权值向量。

图8.11三层BP网络[8]BP算法的基本思想是:预先给定一一对应的输入输出样本集。学习过程由信号的正向传播与误差的反向传播两个过程组成。

正向传播时，输入样本从输入层传入，经过各隐层逐层处理后，传向输出层。若输出层的实际输出与期望的输出(教师信号)不符，则转入误差的反向传播。

将输出误差以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有神经元，获得各层的误差信号，用它们可以对各层的神经元的权值进行调整(关于如何修改权值参见韩立群著作[8])，循环不断地利用输入输出样本集进行权值调整，以使所有输入样本的输出误差都减小到满意的精度。

这个过程就称为网络的学习训练过程。当网络训练完毕后，它相当于映射(表达)了输入输出样本之间的函数关系。

在地球物理勘探中，正演过程可以表示为如下函数:d=f(m)(8.31)它的反函数为m=f-1(d)(8.32)如果能够获得这个反函数，那么就解决了反演问题。

一般来说，难以写出这个反函数，但是我们可以用BP神经网络来映射这个反函数m=f-1(d)。

对于地球物理反问题，如果把观测数据当作输入数据，模型参数当作输出数据，事先在模型空间随机产生大量样本进行正演计算，获得对应的观测数据样本，利用它们对BP网络进行训练，则训练好的网络就相当于是地球物理数据方程的反函数。

可以用它进行反演，输入观测数据，网络就会输出它所对应的模型。BP神经网络在能够进行反演之前需要进行学习训练。训练需要大量的样本，产生这些样本需要大量的正演计算，此外在学习训练过程也需要大量的时间。

但是BP神经网络一旦训练完毕，在反演中的计算时间可以忽略。要想使BP神经网络比较好地映射函数关系，需要有全面代表性的样本，但是由于模型空间的无限性，难以获得全面代表性的样本集合。

用这样的样本训练出来的BP网络，只能反映样本所在的较小范围数据空间和较小范围模型空间的函数关系。对于超出它们的观测数据就无法正确反演。

目前BP神经网络在一维反演有较多应用，在二维、三维反演应用较少，原因就是难以产生全面代表性的样本空间。

用Matlab算BP神经网络的具体算法？

BP神经网络的传递函数一般采用sigmiod函数，学习算法一般采用最小梯度下降法；下面是具体的程序例子：例1采用动量梯度下降算法训练BP网络。

训练样本定义如下：输入矢量为p=[-1-231-115-3]目标矢量为t=[-1-111]解：本例的MATLAB程序如下：closeallclearechoonclc%NEWFF——生成一个新的前向神经网络%TRAIN——对BP神经网络进行训练%SIM——对BP神经网络进行仿真pause%敲任意键开始clc%定义训练样本%P为输入矢量P=[-1,-2,3,1;-1,1,5,-3];%T为目标矢量T=[-1,-1,1,1];pause;clc%创建一个新的前向神经网络net=newff(minmax(P),[3,1],{'tansig','purelin'},'traingdm')%当前输入层权值和阈值{1,1}inputbias=net.b{1}%当前网络层权值和阈值{2,1}layerbias=net.b{2}pauseclc%设置训练参数=50;=0.05;学习速率=0.9;动量系数net.trainParam.epochs=1000;=1e-3;pauseclc%调用TRAINGDM算法训练BP网络[net,tr]=train(net,P,T);pauseclc%对BP网络进行仿真A=sim(net,P)%计算仿真误差E=T-AMSE=mse(E)pauseclcechooff。

神经网络bp算法

BP神经网络误差如何理解