代码+通俗理解图神经网络GNN

1 类比CNN

图神经网络GNN用于解决非欧几里得空间结构的数据结构的表征问题，其本质是依赖图形中边的连接关系表征节点或者图的信息。在说图神经网路是如何实现这一点时，可以先对比卷积神经网络对一般图像的处理过程：

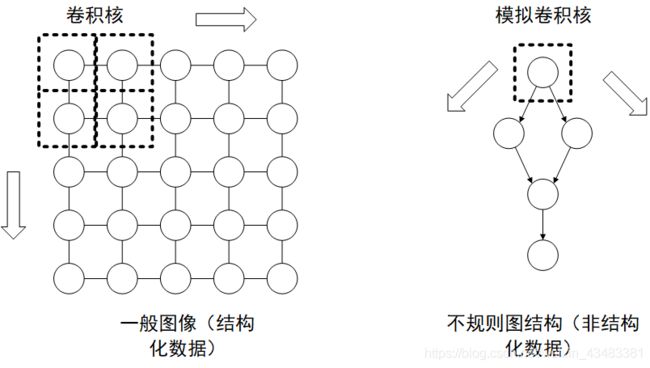
CNN对于图像的处理就是按照从上到下的顺序依次对图像进行卷积，从而提取整个图像的特征；而GNN对于图结构的处理，类似于按照节点为单位，用一个虚拟的卷积核按照节点的连接顺序对图中的节点依次进行处理。因此GNN与CNN的处理过程本质上是一样的。

2 代码理解GNN的训练过程

GNN的“模拟卷积核”在每个节点做的事情就是按照连接关系对每个节点进行聚合：
$new\_node\_embedding=\alpha \ast old\_node\_embedding+\beta \ast f(around\_nodes\_embeddings)$
其中$f$可以看作是对其周围所有节点的一种操作方式，$\alpha ,\beta$以及$f$内部对应的参数都可以成为训练的对象。
这就是GNN做的事情。
talk is cheap
将上述过程形成到代码层面：

import numpy as np

# 这个图是一个有向无环图(DAG)
# -1 代表什么也不连
# 图用二维列表，第一行代表节点编号，第二行为对应节点的指向节点
graph = [
    [0,0,1,2,3],
    [1,2,3,3,4]
]

# 定义5个节点的初始特征值
embeddings = [
    [1,2,3],
    [2,6,5],
    [2,3,7],
    [7,8,6],
    [1,0,0]
]

# 定义聚合的权重w全为1
w = [1,1,1,1,1]

# 下面开始图神经网络的聚合过程（训练过程）
# 在这里每个节点只按照方向聚合一层
for i in range(len(graph[0])):  # 每个节点
    # 先寻找指向节点i的节点们
    temp_roots = []
    for j, eve in enumerate(graph[1]):
        if eve == i:
            temp_roots.append(graph[0][j])
    temp_roots.append(i)
    # 此时temp_roots存储了节点i的根节点以及节点i自己的编号
    around = [
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]
    ]
    # 将temp_roots中的几点对应的around替换成当前的embedding
    for every_node_id in temp_roots:
        around[every_node_id] = embeddings[every_node_id]
    # 开始更新节点i的特征：自己之前的特征+周围节点特征的平均
    embeddings[i] = np.matmul(np.array(w),np.array(around))

# 输出更新一层后的embeddings
print(embeddings)

3 总结

1） GNN 一般处理的任务是图分类或者节点分类，可以看出GNN一般的处理过程是对节点特征进行的训练。在训练获得图形的节点特征之后，可以通过对所有节点进行max、平均值等池化方式来表示整个图的特征。

2）GNN中的NN学习的是在聚合节点时自己多重要，周围节点多重要，以及周围节点该怎么聚合，这是与图的形状无关的；而NN如何正确学习到这个信息就靠标签或者奖励值了。

3）在搭建GNN网络时，搭建的其实是上面的参数$\alpha ,\beta ,f$的表示方法，因此这是与图的形状无关的。也就是意味着不同形状的图是可以使用一套GNN网络模型训练的，因为不同图形只是连接关系不一样，但是其权重是可以一样的。

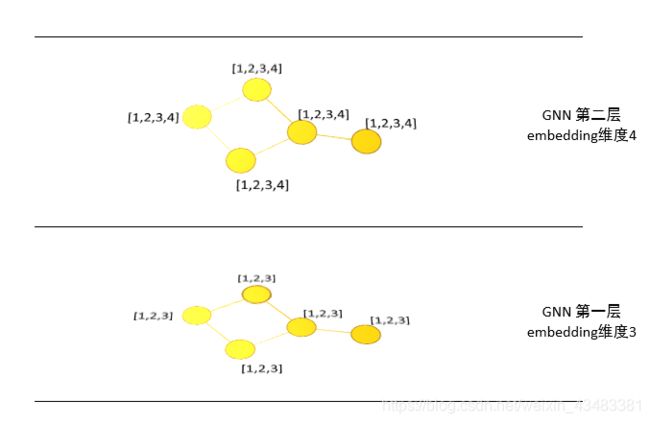
4）值得注意的是，GNN的一层是指节点们的一层embedings的表示，并且大多数GNN都是2-4层。一层相当于对图神经网络在垂直方向进行了一个复制，每一层节点的embeddings维度是一样的，但是不同层的embeddings可以不同：

5）GNN目前大多数使用PyG进行搭建，这方面已经有很多资料了，可以参考其官方文档以及其中对于节点分类的例子:

import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import Planetoid

dataset = Planetoid(root='/tmp/Cora', name='Cora')

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = GCNConv(dataset.num_node_features, 16)
        self.conv2 = GCNConv(16, dataset.num_classes)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index

        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)

        return F.log_softmax(x, dim=1)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

model.train()
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

model.eval()
_, pred = model(data).max(dim=1)
correct = int(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / int(data.test_mask.sum())
print('Accuracy: {:.4f}'.format(acc))