Pytorch中tensor维度和torch.max()函数中dim参数的理解

Pytorch中tensor维度和torch.max()函数中dim参数的理解

---

维度

参考了 https://blog.csdn.net/qq_41375609/article/details/106078474 ，
对于torch中定义的张量，感觉上跟矩阵类似，不过常见的矩阵是二维的。当定义一个多维的张量时，比如使用 a =torch.randn(2, 3, 4) 创建一个三维的张量，返回的是一个

[
     [
            [-0.5166,  0.8298,  2.4580, -1.9504],

            [ 0.1119, -0.3321, -1.3478, -1.9198],

            [ 0.0522, -0.6053,  0.8119, -1.3469]
     ],
     
     [
            [-0.3774,  0.9283,  0.7996, -0.3882],

            [-1.1077,  1.0664,  0.1263, -1.0631],

            [-0.9061,  1.0081, -1.2769,  0.1035]
   ]
]

当使用 a.size() 返回维度结果时，结果为 torch.Size([2, 3, 4])，这里面有三个数值，数值的个数代表维度的个数 ，所以这里有三个维度，可以理解为一个中括号代表一个维度。数值 2 处在第一个位置，第一个位置代表是第一维度,2代表这个维度有两个元素，也就是第一个 [ ] 里面两个元素，3代表在第二个维度，也就是在第一个 [ ] 中的两个元素里面，又有三个元素，依次类推。这里格式十分固定，一旦定义，必须是一个元素里面有两个元素，这两个元素中每个再包含三个元素，再包含，依此类推，否则会报错。类似与树，维数等于相似的树的深度-1（以根为第一层），每一层就是一维。
如生成一个

torch.tensor(
    [
        [
            [1, 2, 3, 4]

            [3, 4, 2, 1]

            [4, 1, 2, 3]
        ]

        [
            [2, 1, 3, 4]

            [3, 4, 2, 1]

            [4, 1, 2, 3]
        ]
    ]
)

方便理解，以下图的形式展示，这里竖线代表一个维度，竖线上所有节点代表同一维度的所有元素。在下面所有图中，同颜色的元素都是按照从上往下按顺序排列的。

---

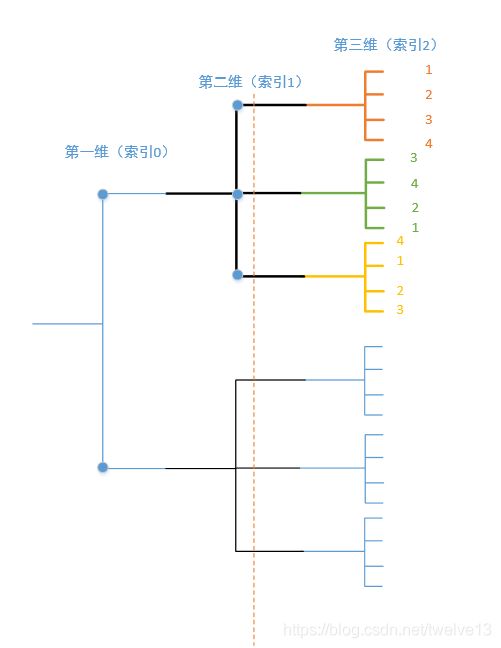
一、dim参数

在使用torch.max()函数和其他的一些函数时，会有dim这个参数。官网中定义使用torch.max()函数时，生成的张量维度会比原来的维度减少一维，除非原来的张量只有一维了. 要减少消去的是哪一维便是由dim参数决定的，dim参数实际上指的是我们计算过程中所要消去的维度。因为在比较时必须要指定使用哪些数字来比较 ，或者进行其他计算，比如 max 使一些数据中只要大的，sum只取和的结果，自然就会删减其他的一些数据从而引起降维。

---

以上面生成的三维的张量为例子，有三个维度，但是维度的数字顺序是 dim = 0， 1， 2；
当指定torch.max(a，dim=0)时，也就是要删除第一个维度，删除第一个维度的话，那还剩下两个维度，也就是dim =1 ，2 。 剩下的两个维度的参数是 3 和 4，那么删除第一个维度后应该剩下torch.tensor(3, 4)这样形式的张量, dim参数可以使用负数，也就是负的索引，与列表中的索引相似，在本例中dim = -1 与dim = 2是一样的。
返回的

values=tensor([[-0.3774,  0.9283,  2.4580, -0.3882],
               [ 0.1119,  1.0664,  0.1263, -1.0631],
               [ 0.0522,  1.0081,  0.8119,  0.1035]]),
indices=tensor([[1, 1, 0, 1], 
                [0, 1, 1, 1],
                [0, 1, 0, 1]]))

从返回的结果看是这种形式，产生这种结果是因为删除了第一个维度那么该返回 3 * 4 这种二维的张量，第一维中两个元素的形式正好是 3 * 4， 那么就将这个维度的两个子元素中的相应的位置的值比较一下大小，那么会生成一个新的 3 * 4 的张量，再返回一下正好可以，indices记录的是 "在比较中胜利的元素“ 原来所属的元素的位置。例如在第一个位置上，-0.3774比 -0.5166大，所以返回-0.3774，-0.3774是在第一维度里面的第二个元素的位置上，这个位置索引为1.剩下的位置的同理。

用树状图理解

图中的不同颜色的三个子元素，在相同位置比较，大的返回形成新的元素，其他位置同理。那么黑色的维度 dim = 1 也就消除了.

---

dim = 0时，如图，两个3*4的子元素张量 相对应的位置 比较大小，剩下一个3 * 4的二维张量

当dim = 2或者 dim = -1，删除的是最后一个维度，在这个例子中吗，将所有的第三维的子元素最大的值返回，返回2 * 3，看起来就像是找所在矩阵一行里面的最大值一样。

values=tensor([[2.4580, 0.1119, 0.8119],
        [0.9283, 1.0664, 1.0081]]),
indices=tensor([[2, 0, 2],
        [1, 1, 1]]))

---

举一个sum()例子,当使用上述使用torch.sum（a，dim = 1），消去第二个维度，剩下一，三维度，也就是2 * 4形状的张量。将第二维上面的三个子元素相同位置的相加，第二维也就不见了，第一维中的两个元素的子元素就从3*4形成了一个1 *4的，总的形状就变成了2 * 4

tensor([[-0.3525, -0.1076,  1.9221, -5.2171],
        [-2.3912,  3.0028, -0.3510, -1.3478]])

---

再举一个例子，使用torch.randn(2, 3, 4, 5) 创建一个四维张量，使用torch.max(dim=-3)，也就是torch.max(dim=1)

torch.tensor([[[[ 0.7106,  1.3332, -1.0423, -0.1609, -0.2846],
	          [ 0.6400,  2.2507, -0.5740, -0.9986,  0.0066],
	          [-0.0527,  1.4097, -0.4439,  0.4846,  1.5418],
	          [ 1.0027,  0.9398,  1.5202, -1.1660, -0.1230]],
	
	         [[ 0.5725, -1.7838, -0.7320, -1.4419,  1.5762],
	          [ 0.6407,  0.0527,  1.7005,  1.6350, -0.2610],
	          [ 1.3307, -0.3210, -1.7203,  0.9050,  0.2442],
	          [ 0.9418, -0.1511,  0.8248, -0.0786, -0.6153]],
	
	         [[ 1.0182,  0.3190, -0.3408, -2.1801, -0.3931],
	          [ 1.2325, -0.3304,  1.0116,  0.0791, -1.1174],
	          [ 0.2331, -0.9062,  0.5680,  1.6061, -1.0933],
	          [ 0.6935, -0.5140, -0.5178,  1.2557,  0.2319]]],
	
	
	        [[[ 1.0916,  0.7171, -0.7936,  1.1741, -0.5457],
	          [-0.6541, -0.6720, -0.7892, -0.6961, -1.1030],
	          [ 1.8680, -0.1746,  0.8455, -1.1021,  0.6855],
	          [ 1.2070, -0.6152, -1.3345, -0.0724,  1.2062]],
	
	         [[-0.5130, -0.5510, -0.8278, -0.2279, -1.4425],
	          [ 0.2073,  1.3065, -0.0326, -1.2566,  0.6097],
	          [-1.0413,  1.2638, -0.8479, -0.0353, -0.7191],
	          [ 0.0662,  0.7683,  0.2145, -0.0988, -2.3348]],
	
	         [[ 0.6631, -0.0040, -0.0681,  1.1681,  1.3904],
	          [-0.1761,  1.4668,  0.9670, -0.5629,  0.2941],
	          [-0.6235,  0.1844, -0.4321, -0.0581, -0.9352],
	          [ 0.1717, -0.9188,  0.3014, -0.0734, -0.1324]]]])
	         

在这里面，当dim = 1，也就是要动第二个维度手，那么删掉它后剩下torch.randn(2，4， 5)形式，那么就
[[ 0.7106, 1.3332, -1.0423, -0.1609, -0.2846],
[ 0.6400, 2.2507, -0.5740, -0.9986, 0.0066],
[-0.0527, 1.4097, -0.4439, 0.4846, 1.5418],
[ 1.0027, 0.9398, 1.5202, -1.1660, -0.1230]]

和
[[ 0.5725, -1.7838, -0.7320, -1.4419, 1.5762],
[ 0.6407, 0.0527, 1.7005, 1.6350, -0.2610],
[ 1.3307, -0.3210, -1.7203, 0.9050, 0.2442],
[ 0.9418, -0.1511, 0.8248, -0.0786, -0.6153]]
还有
[[ 1.0182, 0.3190, -0.3408, -2.1801, -0.3931],
[ 1.2325, -0.3304, 1.0116, 0.0791, -1.1174],
[ 0.2331, -0.9062, 0.5680, 1.6061, -1.0933],
[ 0.6935, -0.5140, -0.5178, 1.2557, 0.2319]]

这三个子元素相应为位置比较大小，大的留下，生成新的张量，列如对于第一个位置，1.0182 比 0.5725 和 0.7106 大，所以它留下，它在元素在要是动手的维度里面的位置索引为2，其它同理
但是这个维度还之前还有一个维度，那么只要对所有的同维度的做相同操作就可以了，所以返回之如下

values=tensor([[[ 1.0182,  1.3332, -0.3408, -0.1609,  1.5762],
         [ 1.2325,  2.2507,  1.7005,  1.6350,  0.0066],
         [ 1.3307,  1.4097,  0.5680,  1.6061,  1.5418],
         [ 1.0027,  0.9398,  1.5202,  1.2557,  0.2319]],

        [[ 1.0916,  0.7171, -0.0681,  1.1741,  1.3904],
         [ 0.2073,  1.4668,  0.9670, -0.5629,  0.6097],
         [ 1.8680,  1.2638,  0.8455, -0.0353,  0.6855],
         [ 1.2070,  0.7683,  0.3014, -0.0724,  1.2062]]]),
indices=tensor([[[2, 0, 2, 0, 1],
         [2, 0, 1, 1, 0],
         [1, 0, 2, 2, 0],
         [0, 0, 0, 2, 2]],

        [[0, 0, 2, 0, 2],
         [1, 2, 2, 2, 1],
         [0, 1, 0, 1, 0],
         [0, 1, 2, 0, 0]]]))