python笔记4：数据归一化（0,1），归至（-1,1）

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

一、pytorch里tensor数据归一化

1.tensor数组全局归一化

数学公式
将数组中的无论正负数值归一化到[0, 1]之间
​
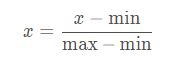
具体操作如下：

1. 定义函数，输入参数为tensor值
2. 求出tensor中最小值
3. 判断最小值是否为负数
4. 若是负数，则tensor所有数值加上最小值的绝对值，此时tensor里无负数，最小值置为0
5. 求出tensor最大值
6. 写出数学公式实现代码
7. 返回值即为全局归一化后的tensor

2.tensor数组指定维度归一化

import torch
def data_normal_2d(orign_data,dim="col"):
	"""
	针对于2维tensor归一化
	可指定维度进行归一化，默认为行归一化
	参数1为原始tensor，参数2为默认指定行，输入其他任意则为列
    """
    if dim == "col":
        dim = 1
        d_min = torch.min(orign_data,dim=dim)[0]
        for idx,j in enumerate(d_min):
            if j < 0:
                orign_data[idx,:] += torch.abs(d_min[idx])
                d_min = torch.min(orign_data,dim=dim)[0]
    else:
        dim = 0
        d_min = torch.min(orign_data,dim=dim)[0]
        for idx,j in enumerate(d_min):
            if j < 0:
                orign_data[idx,:] += torch.abs(d_min[idx])  
                d_min = torch.min(orign_data,dim=dim)[0]
    d_max = torch.max(orign_data,dim=dim)[0]
    dst = d_max - d_min
    if d_min.shape[0] == orign_data.shape[0]:
        d_min = d_min.unsqueeze(1)
        dst = dst.unsqueeze(1)
    else:
        d_min = d_min.unsqueeze(0)
        dst = dst.unsqueeze(0)
    norm_data = torch.sub(orign_data,d_min).true_divide(dst)
    return norm_data

x = torch.randint(low=-10,high=10,size=(3,6))
data_normal_2d(x)
tensor([[1.0000, 0.8182, 0.4545, 0.0000, 0.8182, 0.2727],
        [0.6154, 0.5385, 0.5385, 0.0769, 0.0000, 1.0000],
        [0.4444, 0.3889, 0.0000, 0.2778, 1.0000, 0.5000]])

新torch方法
torch.min() / torch.max()
相较于全局归一化，指定维度使用torch.max(),torch.min()的第二种使用方法
将被求最值的tensor放入括号里，输入一个tensor的时候，如torch.min(x，dim=0)，会返回两个值：第一个是指定维度为行时，各行的最小值组成的tensor；第二个返回的是各最小值的索引tensor。
tensor.unsqueeze()
该方法是将原tensor多扩充一个维度，例如代码中d_min.unsqueeze(1)，是指将d_min从原来的一维向量，扩充其第二维度。

---

二、pytorch里tensor数据归至(-1,1)

因实际数据处理过程中，有些数据本身具有正负属性，此时若直接归一化，会损失数据本身的一些特征。
此时代码里可直接添加一行
norm_data = (norm_data-0.5).true_divide(0.5)
即

    else:
        d_min = d_min.unsqueeze(0)
        dst = dst.unsqueeze(0)
    norm_data = torch.sub(orign_data,d_min).true_divide(dst)
    norm_data = (norm_data-0.5).true_divide(0.5)
    return norm_data

即可将数据归一化至（-1,1）之间

---