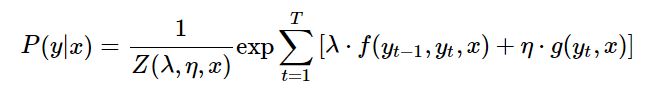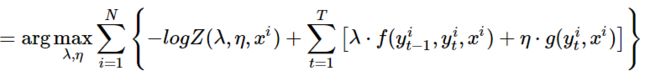[学习日志]白板推导-条件随机场 CRF Conditional Random Field
文章目录
- 背景介绍
-
- 软分类&硬分类
- 硬分类举例
-
- SVM 支持向量机
- PLA 感知机
- LDA 线性判别分析
- 软分类举例
-
- 概率判别模型
- 概率生成模型
- CRF
-
- 概率密度的参数形式
- 概率密度的向量形式
- 求边缘概率 P(Yt|X)
- 参数估计(学习参数)
- 解码问题
- CRF实战
-
- 归一化因子的计算-logsumexp
- 解码-维特比算法
背景介绍
这里主要介绍了一下分类模型的演化过程,优缺点等
因为很多模型没学过,所以就先留着空,以后学全了再回头来补补看吧
软分类&硬分类
- 硬分类:给每一个待分类样本都明确的分配到一个类别,比如SVM就是画一条线泾渭分明。
- 软分类:给每一个待分类样本都计算其属于各个类别的概率,比如朴素贝叶斯就是计算一个条件概率
硬分类举例
SVM 支持向量机
PLA 感知机
LDA 线性判别分析
软分类举例
概率判别模型
比如逻辑回归分类,计算条件概率P(Y|X)
注:逻辑回归可以看作是最大熵模型的特例,至于最大熵模型是啥就以后再补吧
概率生成模型
比如朴素贝叶斯分类,计算联合概率P(X,Y)并通过贝叶斯公式求条件概率
注:朴素贝叶斯分类可以看作隐马尔可夫模型的特例,这个HMM经常出现,后面再补吧
关于生成和判别二者区别可以参考:https://blog.csdn.net/lushilun/article/details/103304592
CRF
如果不做特殊说明,一般认为CRF是指链式CRF,如下图所示
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第1张图片](http://img.e-com-net.com/image/info8/d6643840f82e4c80bd8460e07aa74b0b.jpg)
此模型是判别式模型,也就是说推断的目标是P(Y|X)
X作为模型的输入,是确定的,也就是所谓的“条件”
Y作为模型的预测目标,是一个无向图(马尔可夫随机场),也就是所谓的“随机场”。
关于介绍,可以参考下面这篇文章:
https://zhuanlan.zhihu.com/p/104562658
概率密度的参数形式
在这里我个人是有一个疑惑,就是无向图边缘概率公式中等号左边是边缘概率P(X),为啥能直接套用到CRF的条件概率P(Y|X)呢?
个人理解:其实这个CRF严格意义上不是一个无向图,他只有链式Y的部分是无向图,X部分并不是。而恰恰只有在X部分固定之后,整体才能算是一个无向图,这个时候也就能套用无向图的边缘概率公式了。
CRF多为链式结构,那么其最大团其实是固定的二元组,故公式可以写作:
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第4张图片](http://img.e-com-net.com/image/info8/481fa7611585473a851f537062e79c7e.jpg)
这里还需要补充说明的一点,当i=1时,会有一个Y0,这个节点在CRF上实际时不存在的,但是为了保证数学形式的工整,可以给它凑一个,并不会对模型造成影响。
还要补充说明一点的是,这里为了简化模型,每个极大团的势函数假设为都是相同的,即不存在F1,F2,…,Ft,只存在一个F。这点可能与实际不符,但是为了简化,不得不做出一定的牺牲。(个人理解是这样,也可能确实不需要不同的函数吧)
下面就要探讨,选择什么样的势函数F能够使得模型效果最优化。
这里给出的势函数是下面这个:
![]()
其中:
- Δ(Yt) Δ(Yt-1)称作状态函数
- Δ(Yt,Yt-1)称作转移函数
其实这个是一种很自然的抽象拟合思路:一个有两个变量的函数,这两个变量会怎么影响最终结果呢?无非就是两个变量各自贡献某种影响和两个变量共同贡献某种影响。
.
至于为什么删掉Yt-1,解释如下:
- 在F(Yt-2,Yt-2,X1:T)中也包含了一个Δ(Yt-1),连加之后Δ(Yt-1)的系数就会变成2,而在学习过程中会有参数的引入,还会经历归一化,因此系数是没有影响的。
- λ,η是学习的参数
- f,g是特征函数,是事先人为定义的
特征函数相当于在给当前的这个Y值组合打分,最后算总分
关于特征函数和转移函数更加形象的说明可以参考:
CRF(条件随机场)与Viterbi(维特比)算法原理详解
概率密度的向量形式
这里只是修改一些定义,利用向量点积的连加形式特点2,以简化形式。
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第6张图片](http://img.e-com-net.com/image/info8/26dcfd422ee14e2386db55240d5893ef.jpg)
求边缘概率 P(Yt|X)
做这一步的前提是模型的参数已经确定
(可以认为已经学好了,就是单纯的讲怎么用模型)
也就是说,对于一个输入X,下式已经能顺利得出:
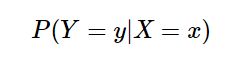
推导过程如下:
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第7张图片](http://img.e-com-net.com/image/info8/f1b1483dba63478cbf7ab1d0e4ace85c.jpg)
因为参数已经确定,也就是说是φ函数是已知且确定的。
那么理论上只需要代入即可完成求解,然而并不行。
复杂度计算如下:
- 设势函数的时间复杂度为O(1)
- 最外围有T-1个积分(连加),每个连加都要对一个词性维度的所有可能进行循环,设词性维度为S,则积分部分的时间复杂度为O(S^T)
- 再加上最内层的连乘,总体时间复杂度为O(T*S^T)
- 基本可以认为这是一个不可解问题
因此需要对问题进一步进行简化。
进行变形如下:
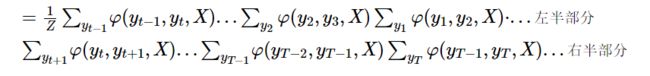
这里左右两部分是并列,中间是点乘符号!!!
左右部分内部是嵌套的多重积分!!!
(感觉是很容易产生误解的地方,注明一下)
细看,这个排列形式不就是很经典的通过积分消元的方法嘛,妈耶
想出来的巨佬真的是人类吗…这操作像是机器人啊
这里一度让我很困惑的地方:
这个顺序的完全打乱的操作合理嘛?
直到我想起来这个式子↓
(凭借我零星的微积分记忆,这个式子应该是对的…吧)
- 利用公式一进行了排序,以消元
- 但是光靠排序是消不干净,因为左右两边消元的顺序是反着的
- 利用公式二将不想关的左右部分拆开,以解决前向后向问题
经过积分消元,最后应该只剩下yt,理论上可以得到下式:
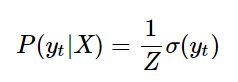
但是变形这么多步骤不是为了简化而简化的,是为了好算才简化。
现在的任务就是搞清楚这个σ函数是啥!
(其实已经搞清楚了,就是上面那一堆积分,
只不过那一堆积分还是有点长,下面继续进行简化)
.
因为左右部分都是嵌套的多重积分,而且积分项(应该是叫这个名字?)结构都是类似的,因此很容易就会让人联想到递推结构,因此做出如下设定:
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第8张图片](http://img.e-com-net.com/image/info8/baa3712080054225825f966c103c7961.jpg)
通过上式,做出归纳如下:
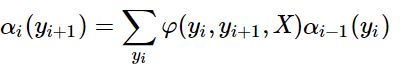
.
右侧同理,稍有不同,不再重复
至此成功将之前复杂的T重积分转换为了递归形式,降低了复杂度
(这不也一样积分嘛,不过既然大佬说简化了,就肯定简化了)
参数估计(学习参数)
样本数据的形式(以词性标注为例子):已标注的句子
用数学符号形式表示如下:

其中:
- N为句子个数,i为句子的编号
- X,Y都是T维向量(T是句子长度?应该是可变的)
- P(Yi|Xi)是单个句子分词正确的概率
- 因为假设句子之间相互独立,因此将所有句子连乘
- 最终也就是让所有句子分对的概率都尽可能高
至此表达式中就都是已知函数,则可通过优化方法进行求解。
解码问题
所谓的解码问题,也就是求解:y’=argmax P(y|x’)
使用到了维特比算法,具体可以参考HMM部分的讲解
二者的解码部分基本一致
CRF实战
实战是对理论学习的检验,而检验结果往往都是不合格的。
即便我写这篇BLOG的上半部分时信心满满已经理解了CRF的大致内容,但是实际上并没有,而且过了几天之后理解的部分也忘的差不多了。
所以实战也是很好的复习和加深理解的机会,以下为复习参考:
Pytorch Bi-LSTM + CRF 代码详解
CRF(条件随机场)与Viterbi(维特比)算法原理详解
Bi-LSTM-CRF for Sequence Labeling
Bi-LSTM Conditional Random Field Discussion
复习时发现,在机器学习中使用更多的是下面这个形式的公式:
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第11张图片](http://img.e-com-net.com/image/info8/e9075c334b304e7693d335596af50a73.jpg)
而且一般都是讲核心部分:
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第12张图片](http://img.e-com-net.com/image/info8/050aae74908243a1a8e8b288501ab604.jpg)
- E状态函数:在这里就是LSTM的输出,为T维向量,各维度为概率值。
- T转移函数:人工定义的函数组(转移矩阵),表示ij序列连续的概率。
条件概率也就是转移函数和状态函数的值加和,然后再做softmax做归一化,见下图:
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第13张图片](http://img.e-com-net.com/image/info8/bd2300c5b974487da07185612b07ecfe.jpg)
归一化因子的计算-logsumexp
因为Y的可能序列有指数级的可能性,因此顺序计算归一化因子是很难的,所以这里采用了递归的思想,见下图,具体参考原博文(链接在上面)。
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第14张图片](http://img.e-com-net.com/image/info8/19ff8621ba3648f7b1eea80b0371a703.jpg)
解码-维特比算法
因为模型只能算P(Y|X),而实际应用中的目的往往是argmax P(Y|X)
因此存在一个额外的解码步骤,也就是找最大的问题
这种序列固定,求最大概率,其实是很经典的维特比算法,见下图
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第15张图片](http://img.e-com-net.com/image/info8/f7afc919db404f1b8484afbe2338d075.jpg)
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第2张图片](http://img.e-com-net.com/image/info8/3a59c0c1b4334a5dae13cc8ef75cf0a8.jpg)
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第3张图片](http://img.e-com-net.com/image/info8/701b9ef405c9489f9a06b046de3dc3d4.jpg)
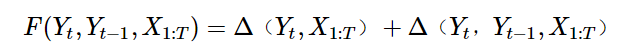
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第5张图片](http://img.e-com-net.com/image/info8/c2c16aa969204c629418b09eee6c0cbd.jpg)
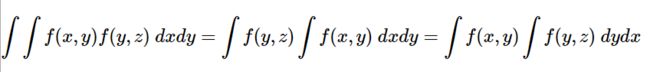
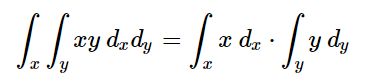
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第9张图片](http://img.e-com-net.com/image/info8/8e64ecc8c7d64430a9d3170799839d9d.jpg)
![[学习日志]白板推导-条件随机场 CRF Conditional Random Field_第10张图片](http://img.e-com-net.com/image/info8/ccd0da04e4f6496886e920f965ce75be.jpg)