矩阵论-定义、符号、以及相关理论
Directory
- 矩阵的秩 (rank)
- 矩阵内积 (Inner Product of Matrices)
-
- Cauchy-Shwarz inequality
- 哈达玛积 (Hadamard Product )
- 克罗内克积(Kronecker Product )
- 向量的范式
-
- 1. 向量范式的定义
- 2. L 1 L_1 L1范式、L2范式、Infinity范式
-
- 1). L 1 L_1 L1-morm
- 2). L 2 L_2 L2-morm
- 3). L ∞ L_\infty L∞-morm
- 矩阵范式
- 黑塞矩阵(Hessian Matrix)
-
- 定义
- 作用
- 函数的黑塞矩阵
-
- 一元函数的泰勒展开式
- 二元函数的黑塞矩阵
- 多元函数的黑塞矩阵
- 利用黑塞矩阵判定多元函数的极值
-
- 例子
矩阵的秩 (rank)
符号: r ( A ) , r k ( A ) , o r r a n k ( A ) r(A),rk(A), \ or \ rank(A) r(A),rk(A), or rank(A)
定义:在线性代数中,一个矩阵A的列秩是A的线性独立的纵列的极大数目。类似地,行秩是A的线性无关的横行的极大数目。即如果把矩阵看成一个个行向量或者列向量,秩就是这些行向量或者列向量的秩,也就是极大无关组中所含向量的个数。
MATLAB求秩函数: rank()
矩阵内积 (Inner Product of Matrices)
符号: ⟨ . , . ⟩ \langle., .\rangle ⟨.,.⟩
目的:度量长度。
定义:列向量 a \mathbf{a} a与行向量 b \mathbf{b} b的内积是指:组成 a \mathbf{a} a的第一个元素与组成 b \mathbf{b} b的第一个元素的乘积,依次,m个这样的乘积的加和。例如,
< a , b > = ( a 1 a 2 ) ( b 1 b 2 ) = a 1 b 1 + a 2 b 2 <\mathbf{a},\mathbf{b}>= \left(\begin{array}{c} a_{1} \\ a_{2} \end{array}\right) \left(\begin{array}{ll} b_{1} & b_{2} \end{array}\right) =a_{1} b_{1} + a_{2} b_{2} <a,b>=(a1a2)(b1b2)=a1b1+a2b2
矩阵 A \mathbf{A} A与矩阵 B \mathbf{B} B的内积是指:组成 A \mathbf{A} A的第一个向量与组成 B \mathbf{B} B的第一个向量的内积,依次,m个这样的内积的加和。
< A , B > = ∑ i = 1 n ∑ j = 1 n a i j ∗ b i j <\mathbf{A},\mathbf{B}>=\sum^n_{i=1}\sum^n_{j=1}a_{ij}*b_{ij} <A,B>=i=1∑nj=1∑naij∗bij
例如
< A , B > = ( a 11 a 12 a 21 a 22 ) ( b 11 b 12 b 21 b 22 ) = ( a 11 + b 11 a 12 + b 12 a 21 + b 21 a 22 + b 22 ) <\mathbf{A},\mathbf{B}>= \left(\begin{array}{c} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right) \left(\begin{array}{ll} b_{11} & b_{12} \\ b_{21} & b_{22} \end{array}\right) =\left(\begin{array}{ll} a_{11}+b_{11} & a_{12}+b_{12} \\ a_{21}+b_{21} & a_{22}+b_{22} \end{array}\right) <A,B>=(a11a21a12a22)(b11b21b12b22)=(a11+b11a21+b21a12+b12a22+b22)
另一种定义: 令 V V V 是定义在场 F \mathbf{F} F ( F = R o r C \mathbf{F} = \mathbf{R} \ or \ \mathbf{C} F=R or C)上的向量空间。 如果对于任意 x , y , z ∈ V x, y, z \in V x,y,z∈V 和 c ∈ F c\in \mathbf{F} c∈F,函数 < ⋅ , ⋅ > : V × V → F \left< \cdot ,\cdot \right>:V\times V\to \mathbf{F} ⟨⋅,⋅⟩:V×V→F满足下列条件,则它是一个内积(inner product)。
( 1 ) ⟨ x , x ⟩ ≥ 0 , N o n n e g a t i v i t y ( 非 负 ) ( 1 a ) ⟨ x , x ⟩ = 0 , i f a n d o n l y i f x = 0 P o s i t i v i t y ( 永 正 ) ( 2 ) ⟨ x + y , z ⟩ = ⟨ x , z ⟩ + ⟨ y , z ⟩ , A d d i t i v i t y ( 加 法 ) ( 3 ) < c x , y > = c < x , y > , H o m o g e n e i t y ( 同 质 ) ( 4 ) < x , y > ≤ < y , x > ‾ , H e r m i t i a n P r o p e r t y ( 共 轭 对 称 ) \begin{aligned} &(1) \ \ \ ⟨x,x⟩ \ge 0 , & \mathrm{Nonnegativity}(非负) \\ &(1a) \ ⟨x,x⟩=0, &\mathrm{if \ and \ only \ if \ x=0 \ Positivity}(永正) \\ &(2)\ \ \ ⟨x+y,z⟩=⟨x,z⟩+⟨y,z⟩, &\mathrm{Additivity}(加法) \\ &(3)\ \ \
Cauchy-Shwarz inequality
定理 (Cauchy-Shwarz inequality). < ⋅ , ⋅ > \left< \cdot ,\cdot \right> ⟨⋅,⋅⟩是定义在向量空间 V V V 上的内积,则对于任意 x , y ∈ V x,y\in V x,y∈V
∣ < x , y > ∣ 2 ≤ < x , x > < y , y > {\left |\left< x ,y \right> \right|}^2 \le \left< x ,x \right>\left< y ,y \right> \quad ∣⟨x,y⟩∣2≤⟨x,x⟩⟨y,y⟩
当且仅当(if and only if) x 和 y 线性相关(linearly dependent),不等式取等号。
标量形式表示为 ( ∑ i = 1 n x i y i ) 2 ≤ ( ∑ i = 1 n x i 2 ) ( ∑ i = 1 n y i 2 ) (\sum_{i=1}^{n}x_iy_i)^2 \le (\sum_{i=1}^{n}x_i^2 )(\sum_{i=1}^{n}y_i^2) (∑i=1nxiyi)2≤(∑i=1nxi2)(∑i=1nyi2)
Proof. 令 x , y ∈ V x,y\in V x,y∈V,若 x = y = 0 x=y=0 x=y=0,则不等式显然成立,所以假设其中一个是非零向量,不失一般性,假设 y ≠ 0 y\ne 0 y=0,令 v = < y , y > x − < x , y > y v=\left< y ,y \right>x - \left< x ,y \right>y v=⟨y,y⟩x−⟨x,y⟩y,有:
0 ≤ < v , v > = < < y , y > x − < x , y > y , < y , y > x − < x , y > y > = < y , y > 2 < x , x > − < y , y > < x , y > ‾ < x , y > − < x , y > < y , x > < y , y > + < y , y > < x , y > ‾ < x , y > = < y , y > 2 < x , x > − < y , y > ∣ < x , y > ∣ 2 = < y , y > ( < x , x > < y , y > − ∣ < x , y > ∣ 2 ) \begin{aligned} 0\le \left< v,v \right>&=\left< \left< y ,y \right>x - \left< x ,y \right>y ,\left< y ,y \right>x - \left< x ,y \right>y \right> \\ &=\left< y ,y \right>^2 \left< x,x \right> -\left< y,y \right>\overline{ \left< x,y \right>}\left< x,y \right>-\left< x,y \right>\left< y,x \right> \left< y,y \right> + \left< y,y \right>\overline{ \left< x,y \right>}\left< x,y \right> \\ &=\left< y ,y \right>^2\left< x,x \right> - \left< y ,y \right> {\left |\left< x,y \right> \right|}^2 \\ &=\left< y ,y \right>(\left< x,x \right>\left< y ,y \right>-{\left |\left< x,y \right> \right|}^2)\end{aligned} 0≤⟨v,v⟩=⟨⟨y,y⟩x−⟨x,y⟩y,⟨y,y⟩x−⟨x,y⟩y⟩=⟨y,y⟩2⟨x,x⟩−⟨y,y⟩⟨x,y⟩⟨x,y⟩−⟨x,y⟩⟨y,x⟩⟨y,y⟩+⟨y,y⟩⟨x,y⟩⟨x,y⟩=⟨y,y⟩2⟨x,x⟩−⟨y,y⟩∣⟨x,y⟩∣2=⟨y,y⟩(⟨x,x⟩⟨y,y⟩−∣⟨x,y⟩∣2)
因为 y ≠ 0 y\ne 0 y=0,即 < y , y > > 0 \left< y ,y \right> > 0 ⟨y,y⟩>0,则推出 < x , x > < y , y > − ∣ < x , y > ∣ 2 ≥ 0 \left< x,x \right>\left< y ,y \right>-{\left |\left< x,y \right> \right|}^2 \ge 0 ⟨x,x⟩⟨y,y⟩−∣⟨x,y⟩∣2≥0 ,只有当 v = 0 v=0 v=0 的时候,等式成立,即 v = < y , y > x − < x , y > y = 0 v=\left< y ,y \right>x - \left< x ,y \right>y=0 v=⟨y,y⟩x−⟨x,y⟩y=0,也就是说 x x x和 y y y线性依赖。
推论 1.5. 如果 $\left< \cdot ,\cdot \right> 是 定 义 在 实 数 或 者 复 数 域 向 量 空 间 是定义在实数或者复数域向量空间 是定义在实数或者复数域向量空间V$ 上的内积,则函数 ∥ ⋅ ∥ : V → [ 0 , ∞ ) \|\cdot\|:V\to [0,\infty) ∥⋅∥:V→[0,∞), ∥ x ∥ = < x , x > 1 / 2 \|x\|= \left< x,x \right>^{1/2} ∥x∥=⟨x,x⟩1/2是向量空间 V V V 上的一个范式。这样的范式(norm)被称为从内积获得(derived from an inner product)。
哈达玛积 (Hadamard Product )
符号: ∘ \circ ∘
LeTex : \circ
定义:哈达玛积 ( Hadamard product ) 是矩阵的一类运算,若 A = ( a i j ) 和 B = ( b i j ) \boldsymbol{A}=(a_{ij})和\boldsymbol{B}=(b_{ij}) A=(aij)和B=(bij)是两个同阶矩阵,若 c i j = a i j × b i j c_{ij}=a_{ij}×b_{ij} cij=aij×bij,则称矩阵 C = ( c i j ) \boldsymbol{C}=(c_{ij}) C=(cij)为 A \boldsymbol{A} A和 B \boldsymbol{B} B的哈达玛积,记为 A ∘ B \boldsymbol{A} \ \circ \boldsymbol{B} A ∘B,具体为:
[ a 11 b 11 a 12 b 12 ⋯ a 1 n b 1 n a 21 b 21 a 22 b 22 ⋯ a 2 n b 2 n ⋮ ⋮ ⋮ a m 1 b m 1 a m 2 b m 2 ⋯ a m n b m n ] \left[\begin{array}{cccc} a_{11} b_{11} & a_{12} b_{12} & \cdots & a_{1 n} b_{1 n} \\ a_{21} b_{21} & a_{22} b_{22} & \cdots & a_{2 n} b_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{m 1} b_{m 1} & a_{m 2} b_{m 2} & \cdots & a_{m n} b_{m n} \end{array}\right] ⎣⎢⎢⎢⎡a11b11a21b21⋮am1bm1a12b12a22b22⋮am2bm2⋯⋯⋯a1nb1na2nb2n⋮amnbmn⎦⎥⎥⎥⎤
克罗内克积(Kronecker Product )
符号: ⊗ \otimes ⊗
LeTex: \otimes
定义:克罗内克积是两个任意大小的矩阵间的运算,它是张量积的特殊形式。给定 A \boldsymbol{A} A和 B \boldsymbol{B} B,则 A \boldsymbol{A} A和 B \boldsymbol{B} B的克罗内克积是一个在空间 R m p × n q \mathbb{R}^{m p \times n q} Rmp×nq的分块矩阵:
A ⊗ B = [ a 11 B ⋯ a 1 n B ⋮ ⋱ ⋮ a m 1 B ⋯ a m n B ] \boldsymbol{A} \otimes \boldsymbol{B}=\left[\begin{array}{ccc} a_{11} \boldsymbol{B} & \cdots & a_{1 n} \boldsymbol{B} \\ \vdots & \ddots & \vdots \\ a_{m 1} \boldsymbol{B} & \cdots & a_{m n} \boldsymbol{B} \end{array}\right] A⊗B=⎣⎢⎡a11B⋮am1B⋯⋱⋯a1nB⋮amnB⎦⎥⎤
向量的范式
1. 向量范式的定义
定义:令 V V V 是定义在场 F \mathbf{F} F ( F = R \mathbf{F} = \mathbf{R} F=R 或者 C \mathbf{C} C,即实数域或者是复数域)上的向量空间。 如果对于任意的 x , y ∈ V x , y \in V x,y∈V 和 c ∈ F c\in \mathbf{F} c∈F 都满足下面几个条件,则称函数 ∥ ⋅ ∥ : V → R \|\cdot\|:V\to \mathbf{R} ∥⋅∥:V→R 是一个范式 (有时被称为向量范式vector norm)。
( 1 ) ∥ x ∥ ≥ 0 , N o n n e g a t i v i t y ( 非 负 ) ( 1 a ) ∥ x ∥ = 0 , i f a n d o n l y i f x = 0 P o s i t i v i t y ( 永 正 ) ( 2 ) ∥ c x ∥ = ∣ c ∣ ∥ x ∥ , H o m o g e n e i t y ( 同 质 ) ( 3 ) ∥ x + y ∥ ≤ ∥ x ∥ + ∥ y ∥ , T r i a n g l e I n e q u a l i t y ( 三 角 不 等 ) \begin{aligned} &(1) \ \ \ ∥x∥≥0, \quad &\mathrm{Nonnegativity}(非负)\\ &(1a) \ ∥x∥=0, \quad &\mathrm{if \ and \ only \ if \ x=0 \ Positivity}(永正)\\ &(2)\ \ \ ∥cx∥= | c | \|x\|, &\mathrm{Homogeneity}(同质)\\ &(3)\ \ \ ∥x+y∥≤\|x\|+\|y\|, &\mathrm{Triangle \ Inequality}(\mathbf{三角不等})\end{aligned} (1) ∥x∥≥0,(1a) ∥x∥=0,(2) ∥cx∥=∣c∣∥x∥,(3) ∥x+y∥≤∥x∥+∥y∥,Nonnegativity(非负)if and only if x=0 Positivity(永正)Homogeneity(同质)Triangle Inequality(三角不等) (2) Positivity和 (3) Homogeneity保证了对于任意非零向量 x x x,可以正则化到单位向量 u = x ∥ x ∥ u=\frac{x}{\|x\|} u=∥x∥x。
只满足(1),(2),(3)而不满足(1a)的范式称为半范式(seminorm),(1a)保证了只有零向量的范式才是0,非零向量的范式都大于0,而一个非零向量的半范式可以是0。
引理 1.2. ∥ ⋅ ∥ \|\cdot\| ∥⋅∥是定义在实数域或者复数域向量空间 V V V 上的半范式, 则对于任意 x , y ∈ V x, y\in V x,y∈V,有 ∣ ∣ x ∣ − ∣ y ∣ ∣ ≤ ∣ x − y ∣ | |x| − |y|| \le |x − y| ∣∣x∣−∣y∣∣≤∣x−y∣
Proof. 即证明 ± ( ∥ x ∥ − ∥ y ∥ ) ≤ ∥ x − y ∥ \pm (\|x\| − \|y\|) \le \|x − y\| ±(∥x∥−∥y∥)≤∥x−y∥
( 1 ) ∥ x ∥ = ∥ x − y + y ∥ ≤ ∥ x − y ∥ + ∥ y ∥ ⇒ ∥ x − y ∥ ≥ ∥ x ∥ − ∥ y ∥ ( 2 ) ∥ y ∥ = ∥ y − x + x ∥ ≤ ∥ y − x ∥ + ∥ x ∥ = ∥ x − y ∥ + ∥ x ∥ ⇒ ∥ x − y ∥ ≥ ∥ y ∥ − ∥ x ∥ \begin{aligned} (1)& \ \|x\| =\|x-y+y\| \le \|x-y\|+\|y\| \\ &\Rightarrow \|x-y\| \ge \|x\| - \|y\| \\ (2) & \ \|y\| =\|y-x+x\| \le \|y-x\|+\|x\| = \|x-y\|+\|x\|\\ &\Rightarrow \|x-y\| \ge \|y\| - \|x\| \\ \end{aligned} (1)(2) ∥x∥=∥x−y+y∥≤∥x−y∥+∥y∥⇒∥x−y∥≥∥x∥−∥y∥ ∥y∥=∥y−x+x∥≤∥y−x∥+∥x∥=∥x−y∥+∥x∥⇒∥x−y∥≥∥y∥−∥x∥
2. L 1 L_1 L1范式、L2范式、Infinity范式
1). L 1 L_1 L1-morm
C n \mathbf{C}^n Cn上的和范式(sum norm),也叫 L 1 L_1 L1-范式( L 1 L_1 L1-norm),定义如下:
∥ x ∥ 1 = ∣ x 1 ∣ + ⋯ + ∣ x n ∣ \|x\|_1=|x_1|+\cdots+|x_n| ∥x∥1=∣x1∣+⋯+∣xn∣ 其通常也被称为曼哈顿范式(Manhattan norm)。
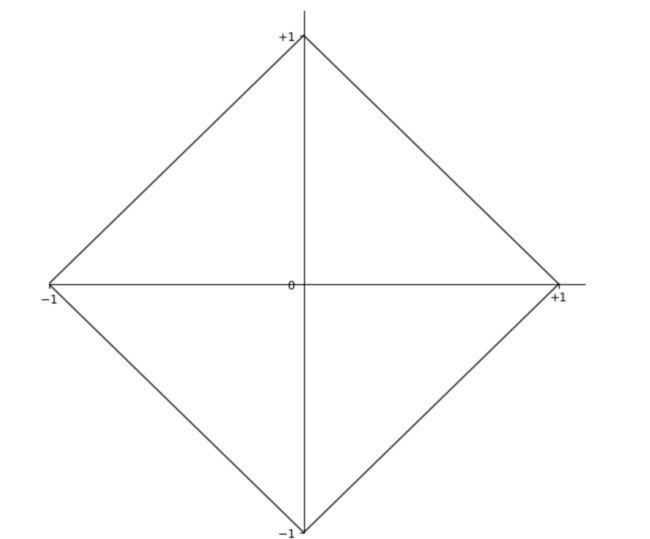
例如:以二维向量 v = ( v 1 , v 2 ) \mathbf{v}=(v_1, v_2) v=(v1,v2)举例,范式的值恰好为1的图像如下,其中横轴代表 v 1 v_1 v1,纵轴代表 v 2 v_2 v2:
L 1 L_1 L1范式,即 ∥ v ∥ 1 = ∣ v 1 ∣ + ∣ v 2 ∣ = 1 \|v\|_1=|v_1|+|v_2|=1 ∥v∥1=∣v1∣+∣v2∣=1
2). L 2 L_2 L2-morm
一个向量 x = [ x 1 , . . . , x n ] T ∈ C n x=[x_1,...,x_n]^T\in \mathbf{C}^n x=[x1,...,xn]T∈Cn的欧几里得范式(Euclidean norm),也叫 L 2 L_2 L2范式( L 2 L_2 L2-norm),定义如下:
∥ x ∥ 2 = ( ∣ x 1 ∣ 2 + ⋯ + ∣ x n ∣ 2 ) 1 / 2 \|x\|_2=(|x_1|^2+\cdots+|x_n|^2)^{1/2} ∥x∥2=(∣x1∣2+⋯+∣xn∣2)1/2 经常使用 ∥ x − y ∥ 2 \|x-y\|_2 ∥x−y∥2来衡量两个点 x , y ∈ C n x,y\in \mathbf{C}^n x,y∈Cn的欧几里得距离(Euclidean distance)。
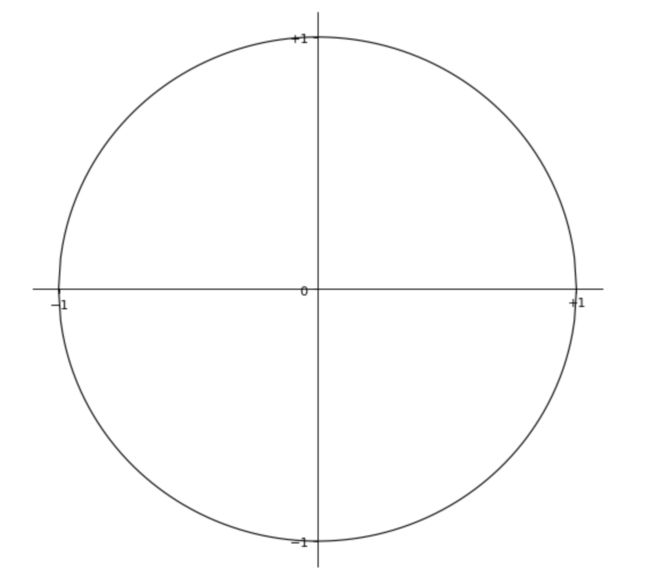
例如: L 2 L_2 L2范式,即 ∥ v ∥ 2 = ∣ v 1 ∣ 2 + ∣ v 2 ∣ 2 = 1 \|v\|_2=\sqrt{|v_1|^2+|v_2|^2}=1 ∥v∥2=∣v1∣2+∣v2∣2=1
3). L ∞ L_\infty L∞-morm
C n C^n Cn上的max norm( l ∞ l_\infty l∞ -norm)为:
∥ x ∥ ∞ = max { ∣ x 1 ∣ , ⋯ , ∣ x n ∣ } \|x\|_\infty= \max \{|x_1|,\cdots,|x_n| \} ∥x∥∞=max{∣x1∣,⋯,∣xn∣} 一般的, C n \mathbf{C}^n Cn 上的 l p l_p lp-norm定义为:
∥ x ∥ p = ( ∣ x 1 ∣ p + ⋯ + ∣ x n ∣ p ) 1 / p , p ≥ 1 \|x\|_p=(|x_1|^p+\cdots+|x_n|^p)^{1/p},\quad p\ge 1 ∥x∥p=(∣x1∣p+⋯+∣xn∣p)1/p,p≥1
例如:Infinity范式,即 ∥ v ∥ ∞ = max { ∣ v 1 ∣ , ∣ v 2 ∣ } = 1 \|v\|_\infty= \max \{|v_1|,|v_2| \}=1 ∥v∥∞=max{∣v1∣,∣v2∣}=1

矩阵范式
Frobenius 范数:
∥ A ∥ F = t r ( A T A ) = ( ∑ i = 1 m ∑ j = 1 m ∣ a i j ∣ 2 ) 1 / 2 , \Vert \mathbf{A} \Vert_F=\sqrt{\mathrm{tr}( \mathbf{A}^{\mathrm{T}} \mathbf{A} )}=(\sum_{i=1}^{m}\sum_{j=1}^{m}|a_{ij}|^2)^{1/2}, ∥A∥F=tr(ATA)=(i=1∑mj=1∑m∣aij∣2)1/2,该定义可以看作向量的 Euclidean 范数对按照矩阵各行排列的“长向量”的推广。
谱范数: ∥ A ∥ F = λ max , \Vert \mathbf{A} \Vert_F=\sqrt{ \lambda_{\max} }, ∥A∥F=λmax, λ max \lambda_{\max} λmax 是矩阵 ( A T A ) (\mathbf{A^{\mathrm{T}}A}) (ATA)的最大特征值. 注意:如果 A \mathbf{A} A是对称方阵, ∥ A ∥ = max ( ∣ λ i ( A ) ∣ ) \|\mathbf{A}\|=\max (|\lambda_i(\mathbf{A})|) ∥A∥=max(∣λi(A)∣),其中 λ i ( A ) \lambda_i(\mathbf{A}) λi(A)为 A \mathbf{A} A所有的特征值。
黑塞矩阵(Hessian Matrix)
定义
黑塞矩阵是一个多元函数的二阶偏导数构成的方阵**,描述了函数的局部曲率。
作用
黑塞矩阵常用于牛顿法解决优化问题,利用黑塞矩阵可判定多元函数的极值问题,边缘检测、消除边缘响应等方面的应用,抽取图像特征。大多数目标函数往往很复杂,为了使问题简化,常将目标函数在某点邻域展开成泰勒多项式来逼近原函数,此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵。
函数的黑塞矩阵
一元函数的泰勒展开式
若一元函数 f ( x ) f(x) f(x)在 x ( 0 ) x^{(0)} x(0)点的某个邻域内具有 ( n + 1 ) (n+1) (n+1)阶导数,则在 x ( 0 ) x^{(0)} x(0)点处的泰勒展开式为:
f ( x ) = f ( x ( 0 ) ) + 1 2 f ′ ( x ( 0 ) ) Δ x + f ′ ′ ( x ( 0 ) ) ( Δ x ) 2 + . . . , = f ( x ) 0 ! + f ′ ( x ) 1 ! ( x − x ( 0 ) ) + f ′ ′ ( x ) 2 ! ( x − x ( 0 ) ) 2 + . . . + f ( n ) ( x ) n ! ( x − x ( 0 ) ) n + R n ( x ) \begin{aligned} f(x) &=f(x^{(0)})+\frac{1}{2}f^{'}(x^{(0)})\Delta x+f^{''}(x^{(0)})(\Delta x)^2 + ..., \\ &= \frac{f(x)}{0!} + \frac{f^{'}(x)}{1!}(x - x^{(0)}) + \frac{f^{''}(x)}{2!}(x - x^{(0)})^2 + ...+\frac{f^{(n)}(x)}{n!}(x - x^{(0)})^n +R_n(x) \end{aligned} f(x)=f(x(0))+21f′(x(0))Δx+f′′(x(0))(Δx)2+...,=0!f(x)+1!f′(x)(x−x(0))+2!f′′(x)(x−x(0))2+...+n!f(n)(x)(x−x(0))n+Rn(x) 其中 Δ x = x − x ( 0 ) , \Delta x = x - x^{(0)}, Δx=x−x(0), Δ x 2 = ( x − x ( 0 ) ) 2 , R n ( x ) = f ( n + 1 ) ( θ ) ( n + 1 ) ! ( x − x ( 0 ) ) ( n + 1 ) \Delta x^2 = \left(x - x^{(0)} \right)^2, R_n(x)=\frac{f^{(n+1)}(\theta)}{(n+1)!}(x - x^{(0)})^{(n+1)} Δx2=(x−x(0))2,Rn(x)=(n+1)!f(n+1)(θ)(x−x(0))(n+1), θ ~\theta θ为 x x x与 x ( 0 ) x^{(0)} x(0)之间的某个值.
二元函数的黑塞矩阵
二元函数 f ( x 1 , x 2 ) f(x_1,x_2) f(x1,x2)在 X 0 ( x 1 ( 0 ) , x 2 ( 0 ) ) X_0(x_1^{(0)},x_2^{(0)}) X0(x1(0),x2(0))点处的泰勒展开式为:
f ( X ) = f ( X ( 0 ) ) + [ ∂ f ( X ( 0 ) ) ∂ x 1 Δ x 1 + ∂ f ( X ( 0 ) ) ∂ x 2 Δ x 2 ] + 1 2 [ ∂ 2 f ′ ′ ( X ( 0 ) ) ∂ 2 x 1 ( Δ x 1 ) 2 + ∂ 2 f ′ ′ ( X ( 0 ) ) ∂ 2 x 2 ( Δ x 2 ) 2 + ∂ 2 f ′ ′ ( X ( 0 ) ) ∂ x 1 ∂ x 2 ( Δ x 1 Δ x 2 ) ] + . . . , \begin{aligned} f(X) &= f(X^{(0)})+ \left[ \frac{\partial f (X^{(0)})}{\partial x_1} \Delta x_1 + \frac{\partial f (X^{(0)})}{\partial x_2} \Delta x_2 \right]+ \\ &~~~\frac{1}{2} \left[ \frac{\partial^2 f^{''}(X^{(0)})}{\partial^2 x_1 } (\Delta x_1)^2 + \frac{\partial^2 f^{''}(X^{(0)})}{\partial^2 x_2 } (\Delta x_2)^2 + \frac{\partial^2 f^{''}(X^{(0)})}{\partial x_1 \partial x_2} (\Delta x_1 \Delta x_2) \right] + ..., \end{aligned} f(X)=f(X(0))+[∂x1∂f(X(0))Δx1+∂x2∂f(X(0))Δx2]+ 21[∂2x1∂2f′′(X(0))(Δx1)2+∂2x2∂2f′′(X(0))(Δx2)2+∂x1∂x2∂2f′′(X(0))(Δx1Δx2)]+..., 其中 Δ x 1 = x 1 − x 1 ( 0 ) , \Delta x_1 = x1-x_1^{(0)}, Δx1=x1−x1(0), Δ x 2 = x 2 − x 2 ( 0 ) . \Delta x_2 = x2-x_2^{(0)}. Δx2=x2−x2(0).
将上述展开式写为矩阵形式:
f ( X ) = f ( X ( 0 ) ) + ( ∂ f ∂ x 1 Δ x 1 + ∂ f ∂ x 2 Δ x 2 ) ∣ X ( 0 ) ( Δ x 1 Δ x 2 ) + 1 2 ( Δ x 1 , Δ x 2 ) ( ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ) ∣ X ( 0 ) ( Δ x 1 Δ x 2 ) + . . . , = f ( X ( 0 ) ) + ∇ f ( X ( 0 ) ) T Δ X + 1 2 Δ X T G ( X ( 0 ) ) Δ X + . . . , \begin{aligned} f(X) &= f(X^{(0)})+ \left. \left( \frac{\partial f}{\partial x_1} \Delta x_1 + \frac{\partial f}{\partial x_2} \Delta x_2 \right) \right|_{X^{(0)}} \left( \begin{aligned} \Delta x_1 \\ \Delta x_2 \end{aligned} \right)+ \left.\frac{1}{2} \left( \Delta x_{1}, \Delta x_{2}\right) \left(\begin{array}{cc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} \end{array} \right) \right|_{X^{(0)}} \left(\begin{array}{c} \Delta x_{1} \\ \Delta x_{2} \end{array}\right) + ...,\\ &=f(X^{(0)}) + \nabla f(X^{(0)})^T \Delta X + \frac{1}{2} \Delta X^T G(X^{(0)}) \Delta X + ..., \end{aligned} f(X)=f(X(0))+(∂x1∂fΔx1+∂x2∂fΔx2)∣∣∣∣X(0)(Δx1Δx2)+21(Δx1,Δx2)(∂x12∂2f∂x2∂x1∂2f∂x1∂x2∂2f∂x22∂2f)∣∣∣∣∣X(0)(Δx1Δx2)+...,=f(X(0))+∇f(X(0))TΔX+21ΔXTG(X(0))ΔX+..., 其中 G ( X ( 0 ) ) = ( ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ) ∣ X ( 0 ) , G(X^{(0)}) = \left.\left(\begin{array}{cc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} \end{array} \right) \right|_{X^{(0)}}, G(X(0))=(∂x12∂2f∂x2∂x1∂2f∂x1∂x2∂2f∂x22∂2f)∣∣∣∣∣X(0), Δ X = ( Δ x 1 Δ x 2 ) \Delta X = \left( \begin{aligned} \Delta x_1 \\ \Delta x_2 \end{aligned} \right) ΔX=(Δx1Δx2), G ( X ( 0 ) ) G(X^{(0)}) G(X(0)) 是 f ( x 1 , x 2 ) f(x_1,x_2) f(x1,x2)在 X ( 0 ) X^{(0)} X(0)点处的黑塞矩阵(Hessian Matrix),它是由函数 f ( X ) f(X) f(X)在 X ( 0 ) X^{(0)} X(0)点处的二阶偏导数所组成的方阵.
多元函数的黑塞矩阵
将二元函数的泰勒展开式推广到多元函数,则 f ( x 1 , x 2 , . . . , x n ) f(x_1,x_2,...,x_n) f(x1,x2,...,xn)在 X ( 0 ) X^{(0)} X(0)点处的泰勒展开式的矩阵形式为:
f ( X ) = f ( X ( 0 ) ) + ∇ f ( X ( 0 ) ) T Δ X + 1 2 Δ X T G ( X ( 0 ) ) Δ X + . . . , f(X)=f(X^{(0)}) + \nabla f(X^{(0)})^T \Delta X + \frac{1}{2} \Delta X^T G(X^{(0)}) \Delta X + ..., f(X)=f(X(0))+∇f(X(0))TΔX+21ΔXTG(X(0))ΔX+..., 其中:
(1). ∇ f ( X ( 0 ) ) = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 , . . . , ∂ f ∂ x n , ] ∣ X ( 0 ) T \nabla f(X^{(0)})= \left.\left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2},..., \frac{\partial f}{\partial x_n}, \right] \right|_{X^{(0)}} ^T ∇f(X(0))=[∂x1∂f,∂x2∂f,...,∂xn∂f,]∣∣∣X(0)T,它是 f ( X ) f(X) f(X)在 X ( 0 ) X^{(0)} X(0)点处的梯度.
(2). G ( X ( 0 ) ) = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ] X ( 0 ) G\left(X^{(0)}\right)=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right]_{X^{(0)}} G(X(0))=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f⎦⎥⎥⎥⎥⎥⎤X(0), 它是 f ( X ) f(X) f(X)在 X ( 0 ) X^{(0)} X(0)点处的Hessian Matrix,是由目标函数f在点 X X X处的二阶偏导数组成的 ( n × n ) (n \times n) (n×n)阶对称矩阵.
利用黑塞矩阵判定多元函数的极值
设n多元实函数 f ( x 1 , x 2 , . . . , x n ) f(x_1,x_2,...,x_n) f(x1,x2,...,xn)在点 M 0 ( a 1 , a 2 , . . . , a n ) M_0(a_1,a_2,...,a_n) M0(a1,a2,...,an)的邻域内有二阶连续偏导,若有: ∂ f ∂ x j ∣ ( a 1 , a 2 , . . . , a n ) , j = 1 , 2 , . . . , n \left.\frac{\partial f}{\partial x_j}\right|_{(a_1,a_2,...,a_n)}, j=1,2,...,n ∂xj∂f∣∣∣∣(a1,a2,...,an),j=1,2,...,n 其中Hessian Matrix为 A = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ] A = \left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right] A=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f⎦⎥⎥⎥⎥⎥⎤
则有以下结论:
(1)当 A A A正定矩阵时, f f f在 M 0 ( a 1 , a 2 , . . . , a n ) M_0(a_1,a_2,...,a_n) M0(a1,a2,...,an)处是极小值;
(2)当 A A A负定矩阵时, f f f在 M 0 ( a 1 , a 2 , . . . , a n ) M_0(a_1,a_2,...,a_n) M0(a1,a2,...,an)处是极大值;
(3)当 A A A不定矩阵时, M 0 ( a 1 , a 2 , . . . , a n ) M_0(a_1,a_2,...,a_n) M0(a1,a2,...,an)不是极值点。
(4)当 A A A为半正定矩阵或半负定矩阵时, M 0 ( a 1 , a 2 , . . . , a n ) M_0(a_1,a_2,...,a_n) M0(a1,a2,...,an)是“可疑”极值点,尚需要利用其他方法来判定。
例子
求三元函数 f ( x , y , z ) = x 2 + y 2 + z 2 + 2 x + 4 y − 6 z f(x,y,z)=x^2+y^2+z^2+2x+4y-6z f(x,y,z)=x2+y2+z2+2x+4y−6z的极值。
解: ∵ ∂ f ∂ x = 2 x + 2 = 0 , ∂ f ∂ x = 2 y + 4 y = 0 , ∂ f ∂ x = 2 z − 6 = 0 \because \frac{\partial f}{\partial x}=2x+2=0,\frac{\partial f}{\partial x}=2y+4y=0, \frac{\partial f}{\partial x}=2z-6=0 ∵∂x∂f=2x+2=0,∂x∂f=2y+4y=0,∂x∂f=2z−6=0
∴ \therefore ∴ 函数 f f f的驻点是 ( − 1 , − 2 , 3 ) (-1,-2,3) (−1,−2,3)
又 ∵ \because ∵ A = [ ∂ 2 f ∂ x 2 ∂ 2 f ∂ x ∂ y ∂ 2 f ∂ x 1 ∂ z ∂ 2 f ∂ y ∂ x ∂ 2 f ∂ y 2 ∂ 2 f ∂ y ∂ z ∂ 2 f ∂ z ∂ x ∂ 2 f ∂ z ∂ y ∂ 2 f ∂ z 2 ] = [ 2 0 0 0 2 0 0 0 2 ] A=\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x^{2}} & \frac{\partial^{2} f}{\partial x \partial y} & \frac{\partial^{2} f}{\partial x_{1} \partial z } \\ \frac{\partial^{2} f}{\partial y \partial x } & \frac{\partial^{2} f}{\partial y^{2}} & \frac{\partial^{2} f}{\partial y \partial z } \\ \frac{\partial^{2} f}{\partial z \partial x } & \frac{\partial^{2} f}{\partial z \partial y } & \frac{\partial^{2} f}{\partial z^{2}} \end{array}\right] = \left[\begin{array}{cccc} 2 & 0 & 0 \\ 0 & 2 &0 \\ 0 &0& 2 \end{array}\right] A=⎣⎢⎡∂x2∂2f∂y∂x∂2f∂z∂x∂2f∂x∂y∂2f∂y2∂2f∂z∂y∂2f∂x1∂z∂2f∂y∂z∂2f∂z2∂2f⎦⎥⎤=⎣⎡200020002⎦⎤
∴ \therefore ∴ A A A是正定矩阵,故 ( − 1 , − 2 , 3 ) (-1,-2,3) (−1,−2,3)是极小值点,且极小值为 f ( − 1 , − 2 , 3 ) = − 14. f(-1,-2,3) = -14. f(−1,−2,3)=−14.