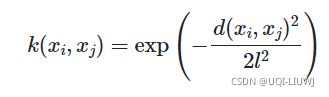sklearn 笔记：高斯过程

class sklearn.gaussian_process.GaussianProcessRegressor(
    kernel=None, 
    *, 
    alpha=1e-10, 
    optimizer='fmin_l_bfgs_b', 
    n_restarts_optimizer=0, 
    normalize_y=False, 
    copy_X_train=True, 
    random_state=None)

理论部分机器学习笔记：高斯过程_UQI-LIUWJ的博客-CSDN博客

1 参数说明

kernel	高斯过程的核函数（无限维高斯分布的协方差矩阵）
alpha	在拟合过程中增加到核矩阵对角线的值。 通过确保计算值形成正定矩阵，这可以防止拟合过程中潜在的数值问题。 它也可以解释为附加高斯测量噪声对训练观测值的方差。 类似于这边的1e-8
n_restarts_optimizer int, default=0	优化器重新启动的次数，用于查找核函数参数，使log边缘似然最大化。 优化器的第一次运行是从核函数的初始参数执行的，其余轮次的参数(如果有的话)是从允许的值的空间中随机采样的。 如果n_restarts_optimizer 大于0，所有的边界都必须是有限的。  注意，n_restarts_optimizer == 0意味着执行一次运行。
normalize_y bool, default=False	是否通过去除均值和缩放到单位方差来标准化目标值y 这在使用零均值、单位方差先验的情况下是推荐的。 注意，逆规则化范化需要在高斯过程预测展现之前完成。
copy_X_train bool, default=True	如果为True，则在对象中存储训练数据的持久副本。 否则，只存储对训练数据的引用，如果外部修改了数据，可能会导致预测发生变化。
random_state	确定用于初始化中心的随机数生成。

2 高斯过程相应方法

fit(X, y)	拟合高斯过程回归模型。
get_params([deep])	或者这个模型的参数
log_marginal_likelihood([theta, …])	返回训练数据theta的log边缘似然值。
predict(X[, return_std, return_cov])	使用高斯过程模型进行预测
sample_y(X[, n_samples, random_state])	从高斯过程中抽取样本并在X处评估
score(X, y[, sample_weight])	返回预测的决定系数
set_params(**params)	人为设置模型的参数

3 高斯过程举例
       

这里说一下RBF核函数的时候的两个参数（但是不确定，欢迎评论区赐教~）

length_scale是RBF式子里l的数值

length_scale_bounds是进行调参的时候，l的取值范围

3.1 构建数据集

# Make an interesting fake function
N = 100
x_min = -10
x_max = +10
# Avoid using linspace so that our data points are NOT equidistant
X = np.sort(np.random.uniform(size=(N))) * (x_max - x_min) + x_min
X = X.reshape(-1, 1) #【100，1】

eta = np.random.normal(loc=0.0, scale=0.5, size=(N))
#【100，】


y_clean = np.sin(X * 2.5) + np.sin(X * 1.0)  + np.multiply(X, X) * 0.05 + 1
#【100，1】
y_clean = y_clean.ravel()
#【100，】

y = y_clean + eta
#[100,]

 3.2 构建高斯过程模型，将数据喂入

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF

kernel = RBF(
    length_scale=1, 
    length_scale_bounds=(1e-2, 1e3))

gpr = GaussianProcessRegressor( kernel,
                               alpha=0.1,
                               n_restarts_optimizer=5,
                               normalize_y=True)
gpr.fit(X,y )

print("LML:", gpr.log_marginal_likelihood())
print(gpr.get_params())
'''
LML: -56.5258341966552
{'alpha': 0.1, 'copy_X_train': True, 'kernel__length_scale': 1, 'kernel__length_scale_bounds': (0.01, 1000.0), 'kernel': RBF(length_scale=1), 'n_restarts_optimizer': 5, 'normalize_y': True, 'optimizer': 'fmin_l_bfgs_b', 'random_state': None}
'''

3.3. 测试其他数据情况

x = np.linspace(x_min - 2.0, x_max + 7.5, N * 2).reshape(-1, 1)
#[200,1]

y_pred, y_pred_std = gpr.predict(
    x, return_std=True)
#[200,],[200,]


import matplotlib.pyplot as plt
plt.figure(figsize=(30, 15))
plt.plot(x, y_pred, label="GP mean")
plt.plot(X, y_clean, '--', label="Original y")
plt.plot(X, y, label="Noisy y")
plt.scatter(X, np.zeros_like(X), marker='x')


plt.fill_between(x.ravel(),
                 y_pred - y_pred_std * 1.9600,
                 y_pred + y_pred_std * 1.9600,
                label="95% confidence interval",
                interpolate=True,
                facecolor='blue',
                alpha=0.5)
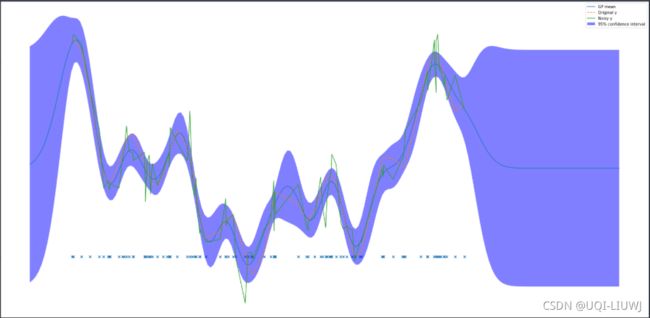
plt.legend()

 可以看到，有先验数据的地方，置信区间范围是很小的