神经网络与深度学习day07-实践:前馈神经网络实现鸢尾花数据集分类
神经网络与深度学习day07-实践:前馈神经网络实现鸢尾花数据集分类
- 深入研究鸢尾花数据集
- 4.5 实践:基于前馈神经网络完成鸢尾花分类
-
- 4.5.1 小批量梯度下降法
- 4.5.2 数据处理
- 4.5.3 模型构建
- 4.5.4 完善Runner类
- 4.5.5 模型训练
- 4.5.6 模型评价
- 4.5.7 模型预测
- 思考题
- 总结
- 参考文献
深入研究鸢尾花数据集
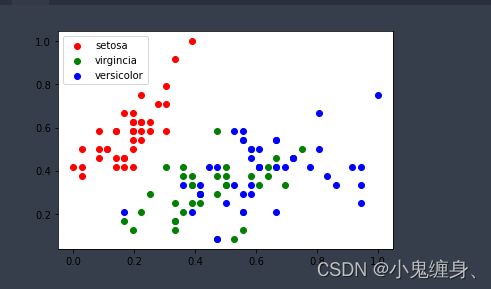
我们再画出第一个特征和第二个特征,第二个特征和第三个特征,第三个特征和第四个特征的分布:
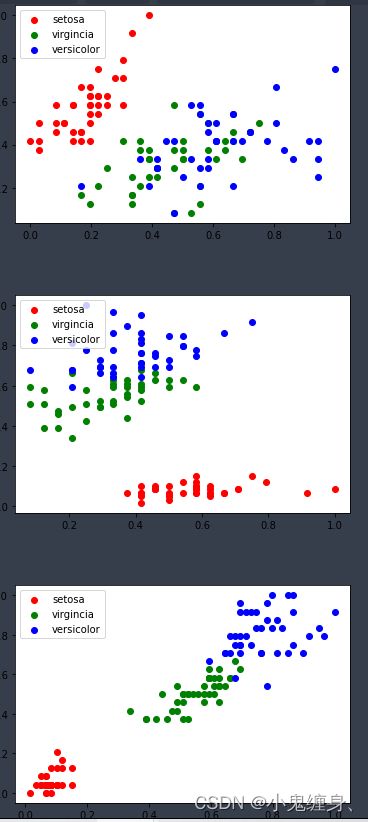
具体代码可以通过看本节4.5.2数据处理 中存在画图代码,由于和数据集相关,放出来估计也不能直接运行出来。
4.5 实践:基于前馈神经网络完成鸢尾花分类
在本实践中,我们继续使用第三章中的鸢尾花分类任务,将Softmax分类器替换为本章介绍的前馈神经网络。
在本实验中,我们使用的损失函数为交叉熵损失;优化器为随机梯度下降法;评价指标为准确率。
4.5.1 小批量梯度下降法
在梯度下降法中,目标函数是整个训练集上的风险函数,这种方式称为批量梯度下降法(Batch Gradient Descent,BGD)。 批量梯度下降法在每次迭代时需要计算每个样本上损失函数的梯度并求和。当训练集中的样本数量 N N N很大时,空间复杂度比较高,每次迭代的计算开销也很大。
为了减少每次迭代的计算复杂度,我们可以在每次迭代时只采集一小部分样本,计算在这组样本上损失函数的梯度并更新参数,这种优化方式称为
小批量梯度下降法(Mini-Batch Gradient Descent,Mini-Batch GD)。
第 t t t次迭代时,随机选取一个包含 K K K个样本的子集 B t \mathcal{B}_t Bt,计算这个子集上每个样本损失函数的梯度并进行平均,然后再进行参数更新。
θ t + 1 ← θ t − α 1 K ∑ ( x , y ) ∈ S t ∂ L ( y , f ( x ; θ ) ) ∂ θ , \theta_{t+1} \leftarrow \theta_t - \alpha \frac{1}{K} \sum_{(\boldsymbol{x},y)\in \mathcal{S}_t} \frac{\partial \mathcal{L}\Big(y,f(\boldsymbol{x};\theta)\Big)}{\partial \theta}, θt+1←θt−αK1(x,y)∈St∑∂θ∂L(y,f(x;θ)),
其中 K K K为批量大小(Batch Size)。 K K K通常不会设置很大,一般在 1 ∼ 100 1\sim100 1∼100之间。在实际应用中为了提高计算效率,通常设置为2的幂 2 n 2^n 2n。
在实际应用中,小批量随机梯度下降法有收敛快、计算开销小的优点,因此逐渐成为大规模的机器学习中的主要优化算法。
此外,随机梯度下降相当于在批量梯度下降的梯度上引入了随机噪声。在非凸优化问题中,随机梯度下降更容易逃离局部最优点。
4.5.2 数据处理
构造IrisDataset类进行数据读取,直接上代码:
导入基本库:
import numpy as np
import torch
from torch.utils.data import Dataset,DataLoader
from sklearn import datasets
import copy
import matplotlib
import matplotlib.pyplot as plt
构造加载数据集函数:
#加载数据集
def load_data(shuffle=True):
"""
加载鸢尾花数据
输入:
- shuffle:是否打乱数据,数据类型为bool
输出:
- X:特征数据,shape=[150,4]
- y:标签数据, shape=[150,3]
"""
#加载原始数据
X = np.array(datasets.load_iris()['data'], dtype=np.float32)
y = np.array(datasets.load_iris()['target'], dtype=np.int64)
X = torch.tensor(X)
y = torch.tensor(y)
#数据归一化
X_min = torch.min(X, axis=0)
X_max = torch.max(X, axis=0)
X = (X-X_min.values) / (X_max.values-X_min.values)
#如果shuffle为True,随机打乱数据
if shuffle:
idx = torch.randperm(X.shape[0])
X_new = copy.deepcopy(X)
y_new = copy.deepcopy(y)
for i in range(X.shape[0]):
X_new[i] = X[idx[i]]
y_new[i] = y[idx[i]]
X = X_new
y = y_new
return X, y
class IrisDataset(Dataset):
def __init__(self, mode='train', num_train=120, num_dev=15):
super(IrisDataset, self).__init__()
# 调用第三章中的数据读取函数,其中不需要将标签转成one-hot类型
X, y = load_data(shuffle=True)
if mode == 'train':
self.X, self.y = X[:num_train], y[:num_train]
elif mode == 'dev':
self.X, self.y = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
else:
self.X, self.y = X[num_train + num_dev:], y[num_train + num_dev:]
def __getitem__(self, idx):
return self.X[idx], self.y[idx]
def __len__(self):
return len(self.y)
def get_(self):
return self.X,self.y
实例化数据并实现可视化:
torch.manual_seed(12)
train_dataset = IrisDataset(mode='train')
dev_dataset = IrisDataset(mode='dev')
test_dataset = IrisDataset(mode='test')
#训练数据可视化
X00,y00 = train_dataset.get_()
x0=X00[y00==0]
x1=X00[y00==1]
x2=X00[y00==2]
for i in [0,1,2]:
plt.scatter(x0[:,i],x0[:,i+1],c='r',marker='o',label='setosa')
plt.scatter(x1[:,i],x1[:,i+1],c='g',marker='o',label='virgincia')
plt.scatter(x2[:,i],x2[:,i+1],c='blue',marker='o',label='versicolor')
plt.legend(loc=2)#把图例放到左上角
plt.show()
可视化结果见本文的深入研究鸢尾花数据集
打印训练集长度:
# 打印训练集长度
print ("length of train set: ", len(train_dataset))
用DataLoader进行封装
# 批量大小
batch_size = 16
# 加载数据
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = DataLoader(dev_dataset, batch_size=batch_size)
test_loader = DataLoader(test_dataset, batch_size=batch_size)
4.5.3 模型构建
构建一个简单的前馈神经网络进行鸢尾花分类实验。其中输入层神经元个数为4,输出层神经元个数为3,隐含层神经元个数为6。代码实现如下:
from torch import nn
# 定义前馈神经网络
class Model_MLP_L2_V3(nn.Module):
def __init__(self, input_size, output_size, hidden_size):
super(Model_MLP_L2_V3, self).__init__()
# 构建第一个全连接层
self.fc1 = nn.Linear(
input_size,
hidden_size
)
# 构建第二全连接层
self.fc2 = nn.Linear(
hidden_size,
output_size
)
# 定义网络使用的激活函数
self.act = nn.Sigmoid()
def forward(self, inputs):
outputs = self.fc1(inputs)
outputs = self.act(outputs)
outputs = self.fc2(outputs)
return outputs
fnn_model = Model_MLP_L2_V3(input_size=4, output_size=3, hidden_size=6)
4.5.4 完善Runner类
基于RunnerV2类进行完善实现了RunnerV3类。其中训练过程使用自动梯度计算,使用DataLoader加载批量数据,使用随机梯度下降法进行参数优化;模型保存时,使用state_dict方法获取模型参数;模型加载时,使用state_dict方法加载模型参数.
由于这里使用随机梯度下降法对参数优化,所以数据以批次的形式输入到模型中进行训练,那么评价指标计算也是分别在每个批次进行的,要想获得每个epoch整体的评价结果,需要对历史评价结果进行累积。这里定义Accuracy类实现该功能。
import torchmetrics as Metric
class Accuracy():
def __init__(self, is_logist=True):
"""
输入:
- is_logist: outputs是logist还是激活后的值
"""
# 用于统计正确的样本个数
self.num_correct = 0
# 用于统计样本的总数
self.num_count = 0
self.is_logist = is_logist
def update(self, outputs, labels):
"""
输入:
- outputs: 预测值, shape=[N,class_num]
- labels: 标签值, shape=[N,1]
"""
# 判断是二分类任务还是多分类任务,shape[1]=1时为二分类任务,shape[1]>1时为多分类任务
if outputs.shape[1] == 1: # 二分类
outputs = torch.squeeze(outputs, axis=-1)
if self.is_logist:
# logist判断是否大于0
preds = troch.can_cast((outputs>=0), dtype=torch.float32)
else:
# 如果不是logist,判断每个概率值是否大于0.5,当大于0.5时,类别为1,否则类别为0
preds = torch.can_cast((outputs>=0.5), dtype=torch.float32)
else:
# 多分类时,使用'paddle.argmax'计算最大元素索引作为类别
preds = torch.argmax(outputs, dim=1).int()
# 获取本批数据中预测正确的样本个数
labels = torch.squeeze(labels, dim=-1)
batch_correct = torch.sum(torch.tensor(preds == labels, dtype=torch.float32)).numpy()
batch_count = len(labels)
# 更新num_correct 和 num_count
self.num_correct += batch_correct
self.num_count += batch_count
def accumulate(self):
# 使用累计的数据,计算总的指标
if self.num_count == 0:
return 0
return self.num_correct / self.num_count
def reset(self):
# 重置正确的数目和总数
self.num_correct = 0
self.num_count = 0
def name(self):
return "Accuracy"
RunnerV3类的代码实现如下:
import torch.nn.functional as F
class RunnerV3(object):
def __init__(self, model, optimizer, loss_fn, metric, **kwargs):
self.model = model
self.optimizer = optimizer
self.loss_fn = loss_fn
self.metric = metric # 只用于计算评价指标
# 记录训练过程中的评价指标变化情况
self.dev_scores = []
# 记录训练过程中的损失函数变化情况
self.train_epoch_losses = [] # 一个epoch记录一次loss
self.train_step_losses = [] # 一个step记录一次loss
self.dev_losses = []
# 记录全局最优指标
self.best_score = 0
def train(self, train_loader, dev_loader=None, **kwargs):
# 将模型切换为训练模式
self.model.train()
# 传入训练轮数,如果没有传入值则默认为0
num_epochs = kwargs.get("num_epochs", 0)
# 传入log打印频率,如果没有传入值则默认为100
log_steps = kwargs.get("log_steps", 100)
# 评价频率
eval_steps = kwargs.get("eval_steps", 0)
# 传入模型保存路径,如果没有传入值则默认为"best_model.pdparams"
save_path = kwargs.get("save_path", "best_model.pdparams")
custom_print_log = kwargs.get("custom_print_log", None)
# 训练总的步数
num_training_steps = num_epochs * len(train_loader)
if eval_steps:
if self.metric is None:
raise RuntimeError('Error: Metric can not be None!')
if dev_loader is None:
raise RuntimeError('Error: dev_loader can not be None!')
# 运行的step数目
global_step = 0
# 进行num_epochs轮训练
for epoch in range(num_epochs):
# 用于统计训练集的损失
total_loss = 0
for step, data in enumerate(train_loader):
X, y = data
# 获取模型预测
logits = self.model(X)
loss = self.loss_fn(logits, y) # 默认求mean
total_loss += loss
# 训练过程中,每个step的loss进行保存
self.train_step_losses.append((global_step,loss.item()))
if log_steps and global_step%log_steps==0:
print(f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")
# 梯度反向传播,计算每个参数的梯度值
loss.backward()
if custom_print_log:
custom_print_log(self)
# 小批量梯度下降进行参数更新
self.optimizer.step()
# 梯度归零
self.optimizer.zero_grad()
# 判断是否需要评价
if eval_steps>0 and global_step>0 and \
(global_step%eval_steps == 0 or global_step==(num_training_steps-1)):
dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)
print(f"[Evaluate] dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}")
# 将模型切换为训练模式
self.model.train()
# 如果当前指标为最优指标,保存该模型
if dev_score > self.best_score:
self.save_model(save_path)
print(f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")
self.best_score = dev_score
global_step += 1
# 当前epoch 训练loss累计值
trn_loss = (total_loss / len(train_loader)).item()
# epoch粒度的训练loss保存
self.train_epoch_losses.append(trn_loss)
print("[Train] Training done!")
# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度
@torch.no_grad()
def evaluate(self, dev_loader, **kwargs):
assert self.metric is not None
# 将模型设置为评估模式
self.model.eval()
global_step = kwargs.get("global_step", -1)
# 用于统计训练集的损失
total_loss = 0
# 重置评价
self.metric.reset()
# 遍历验证集每个批次
for batch_id, data in enumerate(dev_loader):
X, y = data
# 计算模型输出
logits = self.model(X)
# 计算损失函数
loss = self.loss_fn(logits, y).item()
# 累积损失
total_loss += loss
# 累积评价
self.metric.update(logits, y)
dev_loss = (total_loss/len(dev_loader))
dev_score = self.metric.accumulate()
# 记录验证集loss
if global_step!=-1:
self.dev_losses.append((global_step, dev_loss))
self.dev_scores.append(dev_score)
return dev_score, dev_loss
# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度
@torch.no_grad()
def predict(self, x, **kwargs):
# 将模型设置为评估模式
self.model.eval()
# 运行模型前向计算,得到预测值
logits = self.model(x)
return logits
def save_model(self, save_path):
torch.save(self.model.state_dict(), save_path)
def load_model(self, model_path):
model_state_dict = torch.load(model_path)
self.model.state_dict(model_state_dict)
4.5.5 模型训练
实例化RunnerV3类,并传入训练配置,代码实现如下:
import torch.optim as opt
lr = 0.2
# 定义网络
model = fnn_model
# 定义优化器
optimizer = opt.SGD(model.parameters(),lr)
# 定义损失函数。softmax+交叉熵
loss_fn = F.cross_entropy
# 定义评价指标
metric = Accuracy(is_logist=True)
runner = RunnerV3(model, optimizer, loss_fn, metric)
使用训练集和验证集进行模型训练,共训练150个epoch。在实验中,保存准确率最高的模型作为最佳模型。代码实现如下:
# 启动训练
log_steps = 100
eval_steps = 50
runner.train(train_loader, dev_loader,
num_epochs=150, log_steps=log_steps, eval_steps = eval_steps,
save_path="best_model.pdparams")
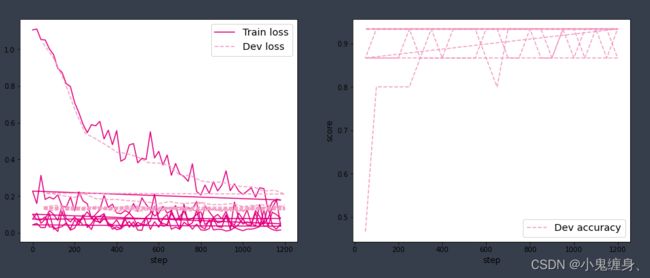
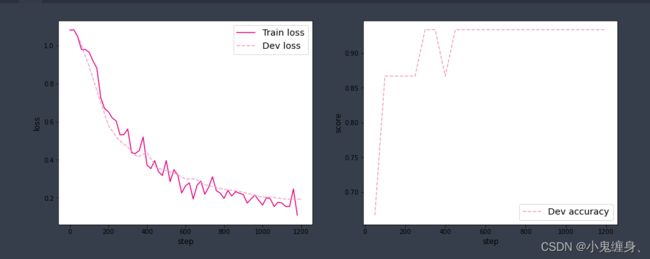
训练结果示意:
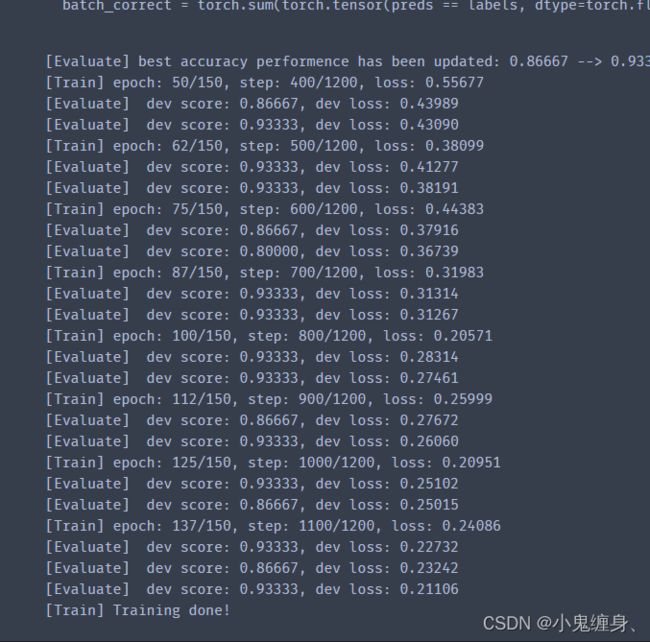
从结果上看,验证集的准确率达到了0.9333,误差仅有0.21106结果还是比较不错的。
可视化观察训练集损失和训练集loss变化情况。
import matplotlib.pyplot as plt
# 绘制训练集和验证集的损失变化以及验证集上的准确率变化曲线
def plot_training_loss_acc(runner, fig_name,
fig_size=(16, 6),
sample_step=20,
loss_legend_loc="upper right",
acc_legend_loc="lower right",
train_color="#e4007f",
dev_color='#f19ec2',
fontsize='large',
train_linestyle="-",
dev_linestyle='--'):
plt.figure(figsize=fig_size)
plt.subplot(1,2,1)
train_items = runner.train_step_losses[::sample_step]
train_steps=[x[0] for x in train_items]
train_losses = [x[1] for x in train_items]
plt.plot(train_steps, train_losses, color=train_color, linestyle=train_linestyle, label="Train loss")
if len(runner.dev_losses)>0:
dev_steps=[x[0] for x in runner.dev_losses]
dev_losses = [x[1] for x in runner.dev_losses]
plt.plot(dev_steps, dev_losses, color=dev_color, linestyle=dev_linestyle, label="Dev loss")
# 绘制坐标轴和图例
plt.ylabel("loss", fontsize=fontsize)
plt.xlabel("step", fontsize=fontsize)
plt.legend(loc=loss_legend_loc, fontsize='x-large')
# 绘制评价准确率变化曲线
if len(runner.dev_scores)>0:
plt.subplot(1,2,2)
plt.plot(dev_steps, runner.dev_scores,
color=dev_color, linestyle=dev_linestyle, label="Dev accuracy")
# 绘制坐标轴和图例
plt.ylabel("score", fontsize=fontsize)
plt.xlabel("step", fontsize=fontsize)
plt.legend(loc=acc_legend_loc, fontsize='x-large')
plt.savefig(fig_name)
plt.show()
plot_training_loss_acc(runner, 'fw-loss.pdf')
4.5.6 模型评价
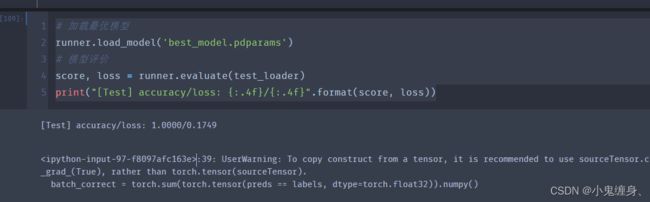
使用测试数据对在训练过程中保存的最佳模型进行评价,观察模型在测试集上的准确率以及Loss情况。代码实现如下:
# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))
4.5.7 模型预测
同样地,也可以使用保存好的模型,对测试集中的某一个数据进行模型预测,观察模型效果。代码实现如下:
# 获取测试集中第一条数据
X, label = test_dataset.get_()
logits = runner.predict(X)
pred_class = torch.argmax(logits[0]).numpy()
label = label[0].numpy()
# 输出真实类别与预测类别
print("The true category is {} and the predicted category is {}".format(label, pred_class))
结果:
The true category is 2 and the predicted category is 2
思考题
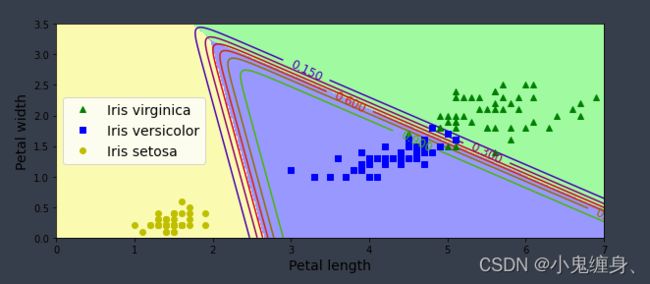
- 对比Softmax分类和前馈神经网络分类。(必做)
softmax分类:
c=0.2时:

c=2.0时
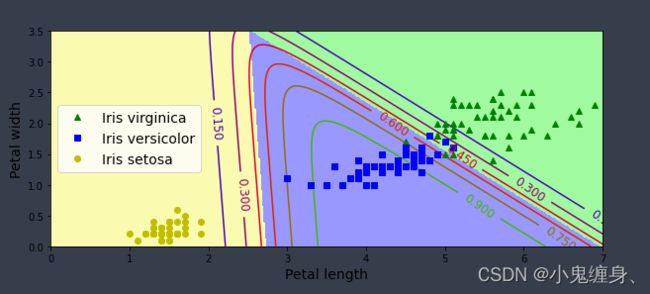
c = 20.0时
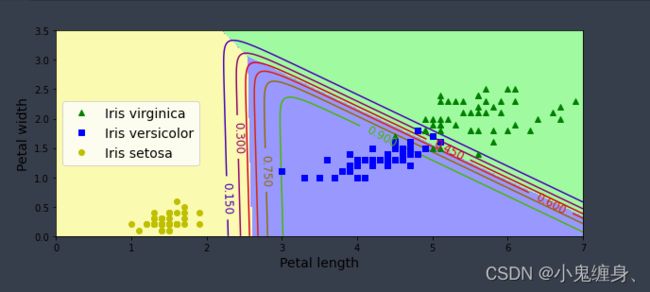
c=100.0时

c=1000.0时
- 自定义隐藏层层数和每个隐藏层中的神经元个数,尝试找到最优超参数完成多分类。(选做)
①自定义隐层神经元的个数:
hidden_size = 8,准确率为0.8667

hidden_size = 7,准确率为0.9333
②调整隐层个数为2
修改代码如下:
from torch import nn
# 定义前馈神经网络
class Model_MLP_L2_V3(nn.Module):
def __init__(self, input_size, output_size, hidden_size1,hidden_size2):
super(Model_MLP_L2_V3, self).__init__()
# 构建第一个全连接层
self.fc1 = nn.Linear(
input_size,
hidden_size1
)
# 构建第二全连接层
self.fc2 = nn.Linear(
hidden_size1,
hidden_size2
)
self.fc3 = nn.Linear(
hidden_size2,
output_size
)
# 定义网络使用的激活函数
self.act = nn.Sigmoid()
def forward(self, inputs):
outputs = self.fc1(inputs)
outputs = self.act(outputs)
outputs = self.fc2(outputs)
outputs = self.act(outputs)
outputs = self.fc3(outputs)
return outputs
fnn_model = Model_MLP_L2_V3(input_size=4, output_size=3, hidden_size1=6,hidden_size2=5)
hidden_size1 = 6,hidden_size2 = 5时,准确率为0.9333

hidden_size1 = 3,hidden_size2 = 2时,准确率为0.9333

hidden_size1 = 2,hidden_size2 = 4时,准确率为0.8667

注意:以上所说的准确率都是训练集的准确率,测试集的准确率都是1.000误差基本稳定在0.5一下,所以说前馈神经网络的训练结果还是比较客观的。
3. 对比SVM与FNN分类效果,谈谈自己看法。(选做)
SVM实现鸢尾花分类的代码:
import numpy as np
from matplotlib import colors
from sklearn import svm
from sklearn.svm import SVC
from sklearn import model_selection
import matplotlib.pyplot as plt
import matplotlib as mpl
# numpy:python第三方库,用于科学计算
# matplotlib:python第三方库,用于进行可视化
# sklearn:python的重要机器学习库,其中封装了大量的机器学习算法,如:分类、回归、降维以及聚类
# 导入鸢尾花数据
from sklearn import datasets
IrisDS = datasets.load_iris()
IrisDS.keys()# 数据集包含的名字
print(IrisDS.target)# 数据标签
print(IrisDS.target_names)# 山鸢尾、变色鸢尾、维吉尼亚鸢尾
print(IrisDS.feature_names)# 花萼长度、花萼宽度、花瓣长度、花瓣宽度
X = IrisDS.data # X是鸢尾花数据集的样本特征
y = IrisDS.target # y是鸢尾花数据集的标签
y = y.ravel()
y
# 以前两个特征(花萼长度、花萼宽度)绘图
X = IrisDS.data[:, :2]
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('speal length', fontsize=20)
plt.ylabel('speal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()
#图中第0类鸢尾花和1、 2两类明显区分开,但1、 2两类区分不明显
# 以后两个特征(花瓣长度、花瓣宽度)进行绘制
X = IrisDS.data[:, 2:]
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "red", marker = "o")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "green", marker = "+")
plt.scatter(X[y == 2, 0], X[y == 2, 1], color = "blue", marker = "x")
plt.xlabel('petal length', fontsize=20)
plt.ylabel('petal width', fontsize=20)
plt.title('Iris names', fontsize=30)
plt.show()
#1、 2两类区分更为明显
X = IrisDS.data[:, :2]
X_train,X_test,y_train,y_test=model_selection.train_test_split(X, #所要划分的样本特征集
y, #所要划分的样本结果
random_state=666, #随机数种子确保产生的随机数组相同
test_size=0.3) #测试样本占比
#SVM分类器构建
clf = svm.SVC(C=0.5, #误差项惩罚系数,默认值是1
kernel='linear', #线性核 kenrel="rbf":高斯核
decision_function_shape='ovr') #决策函数
#***********************训练模型*****************************
clf.fit(X_train, #训练集特征向量,fit表示输入数据开始拟合
y_train) #训练集目标值 ravel()扁平化,将原来的二维数组转换为一维数组
#**************并判断a b是否相等,计算acc的均值*************
def show_accuracy(a, b, tip):
acc = a.ravel() == b.ravel()
print('%s Accuracy:%.3f' %(tip, np.mean(acc)))
def print_accuracy(clf,X_train,y_train,X_test,y_test):
#分别打印训练集和测试集的准确率 score(X_train,y_train):表示输出X_train,y_train在模型上的准确率
print('trianing prediction:%.3f' %(clf.score(X_train, y_train)))
print('test data prediction:%.3f' %(clf.score(X_test, y_test)))
#原始结果与预测结果进行对比 predict()表示对X_train样本进行预测,返回样本类别
show_accuracy(clf.predict(X_train), y_train, 'traing data')
show_accuracy(clf.predict(X_test), y_test, 'testing data')
#计算决策函数的值,表示x到各分割平面的距离,3类,所以有3个决策函数,不同的多类情况有不同的决策函数?
print('decision_function:\n', clf.decision_function(X_train))
# 4.模型评估
print_accuracy(clf,X_train,y_train,X_test,y_test)
def draw(clf, X):
iris_feature = 'sepal length', 'sepal width', 'petal lenght', 'petal width'
# 开始画图
X1_min, X1_max = X[:, 0].min(), X[:, 0].max() #第0列的范围
X2_min, X2_max = X[:, 1].min(), X[:, 1].max() #第1列的范围
X1, X2 = np.mgrid[X1_min:X1_max:200j, X2_min:X2_max:200j] #生成网格采样点 开始坐标:结束坐标(不包括):步长
#flat将二维数组转换成1个1维的迭代器,然后把x1和x2的所有可能值给匹配成为样本点
grid_test = np.stack((X1.flat, X2.flat), axis=1) #stack():沿着新的轴加入一系列数组,竖着(按列)增加两个数组,grid_test的shape:(40000, 2)
print('grid_test:\n', grid_test)
# 输出样本到决策面的距离
z = clf.decision_function(grid_test)
print('the distance to decision plane:\n', z)
grid_hat = clf.predict(grid_test) # 预测分类值 得到【0,0.。。。2,2,2】
print('grid_hat:\n', grid_hat)
grid_hat = grid_hat.reshape(X1.shape) # reshape grid_hat和x1形状一致
#若3*3矩阵e,则e.shape()为3*3,表示3行3列
#light是网格测试点的配色,相当于背景
#dark是样本点的配色
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
#画出所有网格样本点被判断为的分类,作为背景
plt.pcolormesh(X1, X2, grid_hat, cmap=cm_light) # pcolormesh(x,y,z,cmap)这里参数代入
# x1,x2,grid_hat,cmap=cm_light绘制的是背景。
#squeeze()把y的个数为1的维度去掉,也就是变成一维。
plt.scatter(X[:, 0], X[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark) # 样本点
plt.scatter(X_test[:, 0], X_test[:, 1], s=200, facecolor='yellow', zorder=10, marker='+') # 测试点
plt.xlabel(iris_feature[0], fontsize=20)
plt.ylabel(iris_feature[1], fontsize=20)
plt.xlim(X1_min, X1_max)
plt.ylim(X2_min, X2_max)
plt.title('svm in iris data classification', fontsize=30)
plt.grid()
plt.show()
draw(clf, X)
实现效果图:

准确率信息:

可以看出的是,使用SVM进行分类的效果不如FNN的效果好,FNN的训练集的准确率都在0.810以上,而测试集的准确率更是达到了1.000.
- 尝试基于MNIST手写数字识别数据集,设计合适的前馈神经网络进行实验,并取得95%以上的准确率。(选做)
代码:
import torch
import numpy as np
import torch.nn as nn
from torch.autograd import Variable
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
batch_size = 64
learning_rate = 1e-2
num_epoches = 20
data_tf = transforms.Compose([transforms.ToTensor(), transforms.Normalize([0.5],[0.5])])
train_dataset = datasets.MNIST(root = './mnist_data', train = True, transform = data_tf, download = True) #用datasets加载数据集,传入预处理
test_dataset = datasets.MNIST(root = './mnist_data', train = False,transform = data_tf)
train_loader = DataLoader(train_dataset, batch_size = batch_size, shuffle = True) #利用DataLoader建立一个数据迭代器
test_loader = DataLoader(test_dataset, batch_size = batch_size, shuffle = False)
class Batch_Net(nn.Module):
def __init__(self, inputdim, hidden1, hidden2, outputdim):
super(Batch_Net, self).__init__()
self.layer1 = nn.Sequential(nn.Linear(inputdim, hidden1), nn.BatchNorm1d(hidden1), nn.ReLU(True))
self.layer2 = nn.Sequential(nn.Linear(hidden1, hidden2), nn.BatchNorm1d(hidden2), nn.ReLU(True))
self.layer3 = nn.Sequential(nn.Linear(hidden2, outputdim))
def forward(self, x):
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
return x
model = Batch_Net(28*28, 300, 100, 10)
model
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr = learning_rate)
for epoch in range(num_epoches):
train_loss = 0
train_acc = 0
model.train() #这句话会自动调整batch_normalize和dropout值,很关键!
for img, label in train_loader:
img = img.view(img.size(0), -1) #将数据扁平化为一维
img = Variable(img)
label = Variable(label)
# 前向传播
out = model(img)
loss = criterion(out, label)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录误差
train_loss += loss.item()
# 计算分类的准确率
_, pred = out.max(1)
num_correct = (pred == label).sum().item()
acc = num_correct / img.shape[0]
train_acc += acc
print('epoch:{},train_loss:{:.6f},acc:{:.6f}'.format(epoch+1, train_loss/len(train_loader), train_acc/len(train_loader)))
model.eval() #在评估模型时使用,固定BN 和 Dropout
eval_loss = 0
val_acc = 0
for img , label in test_loader:
img = img.view(img.size(0), -1)
img = Variable(img, volatile = True) #volatile=TRUE表示前向传播是不会保留缓存,因为测试集不需要反向传播
label = Variable(label, volatile = True)
out = model(img)
loss = criterion(out, label)
eval_loss += loss.item()
_,pred = torch.max(out, 1)
num_correct = (pred == label).sum().item()
print(num_correct)
eval_acc = num_correct / label.shape[0]
val_acc += eval_acc
print('Test Loss:{:.6f}, Acc:{:.6f}'.format(eval_loss/len(test_loader), val_acc/len(test_loader)))
结果:
Test Loss:0.062413, Acc:0.981091
得到了98%的准确率,还是比较不错的。
总结
- 总结本次实验;
本次实验采用前馈神经网络完成了鸢尾花数据集的分类,同时复习了softmax和svm的分类问题,充分体会到了前馈神经网络功能的强大。
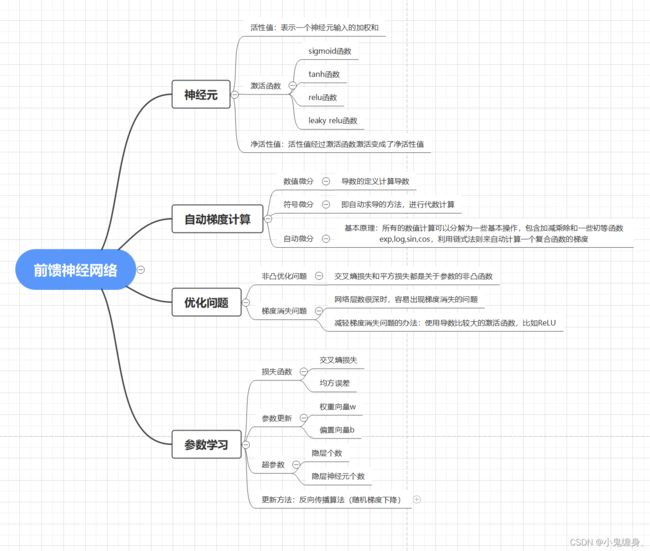
svm在小批量数据及上的分类功能比较强大,而前馈神经网络则适用于大规模的数据集分类。 - 全面总结前馈神经网络,建议画思维导图。
参考文献
NNDL 实验4(下) - HBU_DAVID - 博客园 (cnblogs.com)
2.5. 自动微分 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)
4.7. 前向传播、反向传播和计算图 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)
基于SVM的鸢尾花数据集不同特征的分类
多层全连接神经网络实现minist手写数字分类