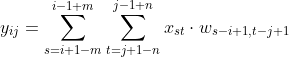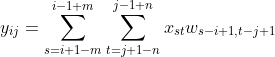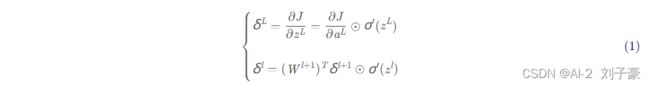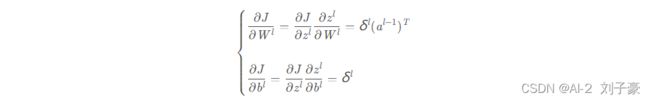NNDL 作业7：第五章课后题（1×1 卷积核 | CNN BP）
目录
习题5-2 证明宽卷积具有交换性,即公式(5.13)
习题5-3 分析卷积神经网络中用1×1的卷积核的作用
习题5-4 对于一个输入为100×100×256的特征映射组，使用3×3的卷积核，输出为100×100×256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1×1的卷积核，先得到100×100×64的特征映射，再进行3×3的卷积，得到100×100×256的特征映射组，求其时间和空间复杂度
习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系
推导CNN反向传播算法（选做）
1. 全连接层
2. 池化层
3. 卷积层
心得体会：
参考博客：
习题5-2 证明宽卷积具有交换性,即公式(5.13)
现有
根据宽卷积定义
为了让x的下标形式和w的进行对换，进行变量替换
令
，
故
.
则
已知
![i \in [1,M]J,J \in [1,N]](http://img.e-com-net.com/image/info8/f690921c38a54fff83eb3f0d39f60e4b.gif){kind=small}
因此对于
由于宽卷积的条件，s和t的变动范围是可行的。
习题5-3 分析卷积神经网络中用1×1的卷积核的作用
- 特征降维，节省计算量
- 增加模型非线性表达能力
举例：从2014年一直延续至今的神经网络设计思想：bottleneck。使用bottleneck（即1 ∗ 1 的卷积核）来进行特征降维，减少特征图的层数，从而减少计算量。
bottleneck的过程如下面两张图片所示：
所以到这里，Naive Inception module就升级为了Inception module。
此时这一个Inception module的计算量为358M ops，相比之前的854M ops，使用“bottleneck”的Inception module的计算量降低了一半多！
习题5-4 对于一个输入为100×100×256的特征映射组，使用3×3的卷积核，输出为100×100×256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1×1的卷积核，先得到100×100×64的特征映射，再进行3×3的卷积，得到100×100×256的特征映射组，求其时间和空间复杂度
时间复杂度：时间复杂度即模型的运行次数。
单个卷积层的时间复杂度：Time~O(M^2 * K^2 * Cin * Cout)
M:输出特征图（Feature Map）的尺寸。
K:卷积核（Kernel）的尺寸。
Cin:输入通道数。
Cout:输出通道数。
注1：为了简化表达式变量个数，统一假设输入和卷积核的形状是正方形，实际中如果不是，则将M ^2替换成特征图的长宽相乘即可；
注2：每一层卷积都包含一个偏置参数（bias），这里也给忽略了。加上的话时间复杂度则为：O(M^2 * K^2 * Cin * Cout+Cout)。
空间复杂度：空间复杂度即模型的参数数量。1*1*256*64+100*100*64+3*3*64*256+100*100*256
单个卷积的空间复杂度：Space~O(K^2 * Cin * Cout+M^2*Cout)
空间复杂度只与卷积核的尺寸K、通道数C相关。而与输入图片尺寸无关。当我们需要裁剪模型时，由于卷积核的尺寸通常已经很小，而网络的深度又与模型的能力紧密相关，不宜过多削减，因此模型裁剪通常最先下手的地方就是通道数。
第一小问：
时间复杂度=100*100*3*3**256*256=5898240000
空间复杂度=3*3**256*256+100*100*256=3149824
第二小问：
时间复杂度=100*100*1*1*256*64+100*100*3*3*64*256=1638400000
空间复杂度=1*1*256*64+100*100*64+3*3*64*256+100*100*256=3363840
习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系
卷积层大家应该都很熟悉了,为了方便说明，定义如下：
- 二维的离散卷积（N=2N=2）
- 方形的特征输入（i1=i2=ii1=i2=i）
- 方形的卷积核尺寸（k1=k2=kk1=k2=k）
- 每个维度相同的步长（s1=s2=ss1=s2=s）
- 每个维度相同的padding (p1=p2=pp1=p2=p)
下图表示参数为 (i=5,k=3,s=2,p=1)(i=5,k=3,s=2,p=1) 的卷积计算过程，从计算结果可以看出输出特征的尺寸为 (o1=o2=o=3)(o1=o2=o=3)。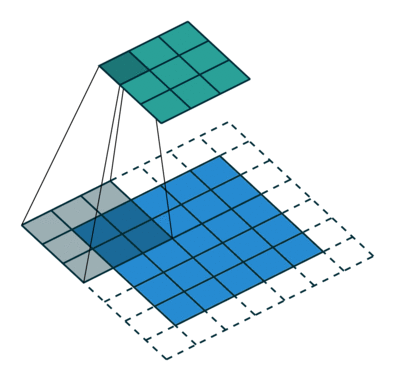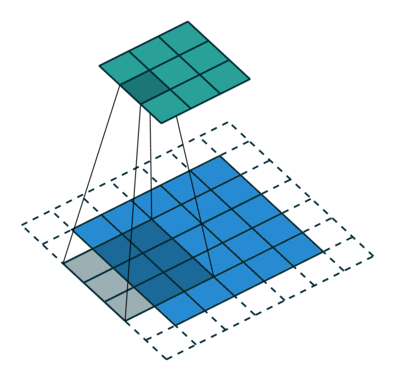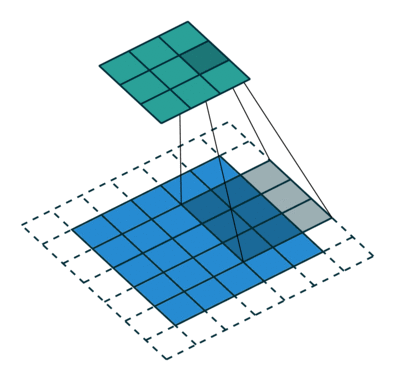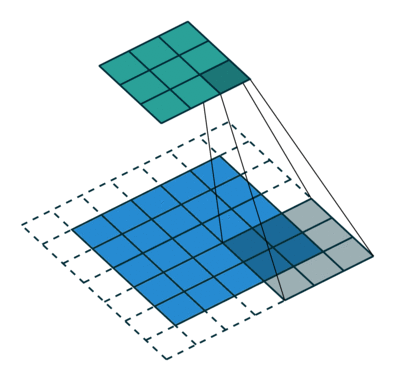
下图表示参数为 (i=6,k=3,s=2,p=1)(i=6,k=3,s=2,p=1) 的卷积计算过程，从计算结果可以看出输出特征的尺寸为 (o1=o2=o=3)(o1=o2=o=3)。
从上述两个例子我们可以总结出卷积层输入特征与输出特征尺寸和卷积核参数的关系为：
o=⌊i+2p−ks⌋+1.o=⌊i+2p−ks⌋+1.其中 ⌊x⌋⌊x⌋ 表示对 xx 向下取整。
考虑如下一个简单的卷积层运算，其参数为 (i=4,k=3,s=1,p=0)(i=4,k=3,s=1,p=0)，输出 o=2o=2。
对于上述卷积运算，我们把上图所示的3×3卷积核展成一个如下所示的[4,16]的稀疏矩阵 CC， 其中非0元素 wi,jwi,j 表示卷积核的第 ii 行和第 jj 列。
我们再把4×4的输入特征展成[16,1]的矩阵 XX，那么 Y=CXY=CX 则是一个[4,1]的输出特征矩阵，把它重新排列2×2的输出特征就得到最终的结果，从上述分析可以看出卷积层的计算其实是可以转化成矩阵相乘的。值得注意的是，在一些深度学习网络的开源框架中并不是通过这种这个转换方法来计算卷积的，因为这个转换会存在很多无用的0乘操作。
通过上述的分析，我们已经知道卷积层的前向操作可以表示为和矩阵CC相乘，那么我们很容易得到卷积层的反向传播就是和CC的转置相乘。
推导CNN反向传播算法（选做）
1. 全连接层
与深度神经网络DNN的反向传播算法一致，辅助变量：
进而求得参数W，b的梯度：
2. 池化层
3. 卷积层
心得体会：
对于宽卷积具有交换性有了深刻的认识，对于1×1卷积核的作用的作用有了补充，原本来并不知道1×1卷积核具有增加模型非线性表达能力，掌握了时间复杂度和空间复杂度的计算过程，原来只知道卷积网络中卷积层的前向计算和反向传播是一种转置关系，但并不知道其原理，经过这次的作业，大体上晓得了。对CNN反向传播算法有了一定的了解，但并未完全掌握，还需再下功夫。
参考博客：
1. 1*1卷积核的作用（bottleneck的作用）
2. 卷积神经网络的时间、空间复杂度以及数据流的变化
3. 卷积与反卷积（转置卷积）关系的公式推导 及其各自的形式
4. 卷积神经网络(CNN)反向传播算法 - 刘建平Pinard - 博客园 (cnblogs.com)