最小二乘法函数拟合原理及matlab实现—数学笔记

最小二乘法函数拟合原理及matlab实现

——数值分析数学笔记

---

如有纰漏，欢迎指正

---

前言

        对大量实验数据 $(x_i,y_i)$ 如何寻找一个合适的函数 $y=f(x)$ 来近似的描述呢？
        所谓 “合适” ：要求 $y=f(x)$ 最能反应数据点的总体趋势
Tips: 第一节和第二节皆是数学推导，可跳过直接看第三节的应用。

---

以下为正文

        既然是分析实验数据 $(x_i,y_i)$ ，那么数据有什么特点及要求呢？

1. 实验数据并不是准确无误，存在误差。
2. 实验数据较多甚至很多。
3. 数据的采样基本能够反应 $x$ 与 $y$ 的对应关系。

  对于第一个特点，假设我们构造出了一个函数，结果发现很多甚至所有的实验数据都不在函数图像上？这合适吗？这很合适！因为带有误差的实验数据落在了函数曲线上，那就说明我们的曲线是存在误差的。如果我们得到的数据（一定不是实验的数据，可能是经过计算得到的数据）能够保证准确无误。那么应该优先考虑通过插值的方法构造函数。
  对于第二个特点，若是实验数据很少，我们能否强行构造函数呢？能，但构造出的函数是没有意义的，它不能体现总体水平。因此我们需要大量的实验数据。
  对于第三个特点，如果 $x$ 与 $y$ 本就毫无关系，又何谈“构造函数来近似描述”呢？

  假设我们的实验数据具备以上特征，要如何才能构造出了一个函数 最能反应数据点的总体趋势“ 呢？什么叫最能？ 你画 一条拟合函数，我画一条拟合函数都可以说是“最能”，因此我们需要确定一个标准。

一、拟合标准

实验值：$y_i$

拟合值：$y_i^{\ast }$

偏差（拟合值与实验值之差）：$r_i=y_i-y_i^{\ast }(i=1,2,3,...,m)$ 注意在数理统计中，偏差又称残差，不是误差！

记偏差向量：$\mathbf{r}=(r_1,r_2,...,r_m)$ （这能记录每个数据点的偏差，即总体）

1.使偏差向量满足 $1$ - 范数

数学表达式：$$\sum _{i=1}^m|{\mathbf{r}}_{\mathbf{i}}|=|r_1|+|r_2|+...+|r_m|=min$$

  通俗的讲就是：要求每个实验数据的偏差绝对值之和最小。 这个标准很容易想到，也很合适，但在导出拟合函数的过程中，运算很麻烦，暂且抛弃该标准。

2.使偏差向量满足 $\infty$ - 范数

数学表达式：$$max|{\mathbf{r}}_{\mathbf{i}}|=min$$

  通俗的讲就是：在所有的实验数据 $(r_1,r_2,...,r_n)$ 中找到最大的 $r_{max}$ ，要求这个 $r_{max}$ 最小，即最大的偏差都最小。 既然最大的偏差都最小了，这个标准非常合适。这种拟合方式称之为最佳一致逼近。（但不是本文的内容，也暂不讨论）

3.使偏差向量满足 $2$ - 范数

数学表达式：$$\sqrt{\sum _{i=1}^m{\mathbf{r}}_{\mathbf{i}}^2}=\sqrt{r_1^2+r_2^2+...+r_m^2}=min$$

  通俗的讲就是：先把每个实验数据的偏差求平方，然后要求这些偏差平方的和最小。 这个标准通过平方把偏差放大，又要求偏差的平方之和开根号最小，因此很合适。而且该法在之后导出拟合函数的过程中，运算也不麻烦。这种拟合方式称之为最佳平方逼近。也称曲线拟合的最小二乘法

  自此我们确立了三个拟合的标准。下面就曲线拟合的最小二乘法导出拟合的公式。

---

二、最小二乘法原理

1.最小二乘法 多项式拟合（常用）

  要构造函数，首先确定函数类别。几个基本的函数类：多项式函数、三角函数、指数函数…这里我们选择多项式函数。
  在众多函数类中，为什么选择多项式函数？因为多项式函数的好处多多：运算简便，次数越高拟合结果越好（注意不能过高）

  1.1最小二乘法的多项式拟合公式 推导。

   假设 n 次多项式函数 $P_n(x)=a_0+a_{1}x+a_2{x}^2+...+a_n{x}^n$ 就是想要的拟合函数，那么每个数据的偏差 $r_i$ 可以表示为：

$$r_i=(P_n(x_i)-y_i)(i=1,2,3,...,m)$$

且满足最小二乘（最佳平方逼近）的拟合标准，则有：

$$\sqrt{\sum _{i=1}^m(P_n(x_i)-y_i{)}^2}=min(i=1,2,3,...,m)$$

（这表示m个数据点的偏差平方的和最小

   令$F(a_0,a_1,...,a_n)={\sum }_{i=1}^m(P_n(x_i)-y_i{)}^2$ 注意这里对于函数$F(a_0,a_1,...,a_n)$，未知量是$a_0,a_1,...,a_n$。上述拟合标准等效于：

   当 $a_0,a_1,...,a_n$ 取的何值时，$F(a_0,a_1,...,a_n)$ 取得最小值。

   至此，问题转化为了求多元函数极值点了，首先对多元函数$F(a_0,a_1,...,a_n)$ 求偏导并令导数值为0，求出驻点：
$$\{\begin{array}{llccc}\frac{\partial F(a_0,a_1,...,a_n)}{\partial a_0}=0& & & & \\ \frac{\partial F(a_0,a_1,...,a_n)}{\partial a_1}=0& & & & \\ & & & & ⋮\\ \frac{\partial F(a_0,a_1,...,a_n)}{\partial a_n}=0& & & & \end{array}$$
可导出如下n元线性方程组（省略繁杂的过程）$\Rightarrow$
$$\{\begin{array}{llccc}m{a}_0+({\sum }_{i=1}^m{x}_i)a_1+({\sum }_{i=1}^m{x}_i^2)a_2+...+({\sum }_{i=1}^m{x}_i^n)a_n={\sum }_{i=1}^m{y}_i& & & & \\ ({\sum }_{i=1}^m{x}_i)a_0+({\sum }_{i=1}^m{x}_i^2)a_1+({\sum }_{i=1}^m{x}_i^3)a_2+...+({\sum }_{i=1}^m{x}_i^{(n+1)}{a}_n={\sum }_{i=1}^m{x}_i{y}_i& & & & \\ ({\sum }_{i=1}^m{x}_i^2)a_0+({\sum }_{i=1}^m{x}_i^3)a_1+({\sum }_{i=1}^m{x}_i^4)a_2+...+({\sum }_{i=1}^m{x}_i^{(n+2)}{a}_n={\sum }_{i=1}^m{x}_i^2{y}_i& & & & \\ & & & & ⋮\\ ({\sum }_{i=1}^m{x}_i^n)a_0+({\sum }_{i=1}^m{x}_i^{n+1})a_1+({\sum }_{i=1}^m{x}_i^{n+2})a_2+...+({\sum }_{i=1}^m{x}_i^{(n+n)}{a}_n={\sum }_{i=1}^m{x}_i^n{y}_i& & & & \end{array}$$
这个方程组称之为法方程组，注意到 $F(a_0,a_1,...,a_n)$ 是二次非负函数没有最大值，故驻点必为极小值点。解该法方程组就能得到多项式函数的系数 $a_0,a_1,...,a_n$ ，从而得到拟合函数 $P_n(x)=a_0+a_{1}x+a_2{x}^2+...+a_n{x}^n$

  1.2 结论：

   由此，我们得到了多项式函数拟合的一般方法：
构造$F(a_0,a_1,...,a_n)$ $⟶$求偏导 $⟶$ 解法方程组 $⟶$ 得 $a_0,a_1,...,a_n$ $⟶$ 作为多项式$P_n(x)=a_0+a_{1}x+a_2{x}^2+...+a_n{x}^n$ 对应系数。

  1.3 案例1：

求下面数据表的最小二乘二次拟合多项式：

$x_i$	$y_i$
-1	-0.2209
-0.75	0.3295
-0.5	0.8826
-0.25	1.4392
0	2.0003
0.25	2.5645
0.5	3.1334
0.75	3.7601
1	4.2836

设多项式函数为：$P_n(x)=a_0+a_{1}x+a_2{x}^2$
将数据点带入法方程组：
$$\{\begin{array}{l}9a_0+0_1+3.75a_2=18.1723\\ 0+3.75a_1+0=8.4842\\ 3.75a_0+0+2.7656a_2=7.1673\end{array}$$
解得：$a_0=2.0034,a_1=2.2625,a_2=0.0378$ 故多项式拟合函数为：$P_n(x)=2.0034+2.2625x+0.0378x^2$

2.最小二乘法的一般形式（线性）（非重点）

  有些时候，我们就偏不要用多项式函数拟合，又该怎么办呢？可以仿照上述步骤推导，那样的话，当又换了一个函数类，岂不是又得重新推导，实在麻烦！
因此，这里给出最小二乘法的一般形式。

 2.1 线性最小二乘法的一般形式推导

  设给定数据 $(x_i,y_i)$ ，又 $\left\{{\phi }_k(x)\right\}$ 为点集${\left\{x_i\right\}}_{i=1}^m$上的线性无关族，选取函数$\phi \in \mathbf{\varphi }=span\left\{{\varphi }_0,{\varphi }_1,...,{\varphi }_n\right\}$满足：
$$\sqrt{\sum _{i=1}^m(y_i-\phi (x_i){)}^2}=\sqrt{\underset{h\in \varphi }{\min }\sum _{i=1}^m(y_i-h(x_i){)}^2}$$
其中 $h(x_i)$ 可由$\left\{{\varphi }_0,{\varphi }_1,...,{\varphi }_n\right\}$线性组合得到，即 $h_x=a_0{\varphi }_0+a_1{\varphi }_1+...+a_0{\varphi }_n$

因此：

如上章所述解法，令$F(a_0,a_1,...,a_n)={\sum }_{i=1}^m(y_i-h(x_i){)}^2={\sum }_{i=1}^m(y_i-{\sum }_{k=0}^n{a}_k{\phi }_k(x_i){)}^2$ 求偏导令导数值为零：

$$\{\begin{array}{ll}\frac{\partial F(a_0,a_1,...,a_n)}{\partial a_0}=0& \\ \frac{\partial F(a_0,a_1,...,a_n)}{\partial a_1}=0& \\ & ⋮\\ \frac{\partial F(a_0,a_1,...,a_n)}{\partial a_n}=0& \end{array}$$
如 二.1.1 导出法方程组 $\Rightarrow$
$$\{\begin{array}{llccc}{\sum }_{k=0}^n({\sum }_{i=1}^m{\phi }_k(x_i){\phi }_0(x_i))a_k={\sum }_{i=1}^m{y}_i{\phi }_0(x_i)& & & & \\ {\sum }_{k=0}^n({\sum }_{i=1}^m{\phi }_k(x_i){\phi }_1(x_i))a_k={\sum }_{i=1}^m{y}_i{\phi }_1(x_i)& & & & \\ {\sum }_{k=0}^n({\sum }_{i=1}^m{\phi }_k(x_i){\phi }_2(x_i))a_k={\sum }_{i=1}^m{y}_i{\phi }_2(x_i)& & & & \\ & & & & ⋮\\ {\sum }_{k=0}^n({\sum }_{i=1}^m{\phi }_k(x_i){\phi }_n(x_i))a_k={\sum }_{i=1}^m{y}_i{\phi }_n(x_i)& & & & \end{array}$$
为方便记忆和表示，由向量的运算法则，我们记：
${\phi }_j=({\phi }_j(x_1),{\phi }_j(x_2),{\phi }_j(x_3),...,{\phi }_j(x_m))$   $j=0,1,2,...,n$

$a=(a_0,a_1,...,a_n{)}^T$

$y=(y_0,y_1,...,y_n{)}^T$

$\mathbf{G}$ 矩阵：

$$G=\left(\begin{array}{cccc}{\phi }_0(x_0)& {\phi }_1(x_0)& ...& {\phi }_n(x_0)\\ {\phi }_0(x_1)& {\phi }_1(x_1)& ...& {\phi }_n(x_1)\\ ⋮& & & \\ {\phi }_0(x_m)& {\phi }_1(x_m)& ...& {\phi }_n(x_m)\end{array}\right)$$

可以验证（过程繁琐） 法方程组 即表示为：

$${\mathbf{G}}^T\mathbf{G}a={\mathbf{G}}^{T}y$$
同样的解该法方程组就能得到函数的系数 $a_0,a_1,...,a_n$ 从而构造出一般的拟合函数 $h_x=a_0{\varphi }_0+a_1{\varphi }_1+...+a_0{\varphi }_n$

 2.2 结论

   由此，我们得到了一般函数拟合的一般方法：构造拟合函数的G矩阵---->解法方程组$G^{T}Ga=G^{T}y$----->解得a

 2.3 案例2

求下面数据表的最小二乘指数拟合：
目标拟合函数为：$y(x)=a_0+a_1{e}^x+a_2{e}^{-x}$

$x_i$	$y_i$
0	2
0.1	2.20254
0.2	2.40715
0.3	2.61592
0.4	2.83096
0.5	3.06448
0.6	3.28876

解：
  ① 由题意：${\phi }_0(x)=1,{\phi }_1(x)=e^x,{\phi }_2(x)=e^{-x}$
  ② 先构造G矩阵:
$$G=\left(\begin{array}{ccc}{\phi }_0(x_0)& {\phi }_1(x_0)& {\phi }_2(x_0)\\ {\phi }_0(x_1)& {\phi }_1(x_1)& {\phi }_2(x_1)\\ {\phi }_0(x_2)& {\phi }_1(x_2)& {\phi }_2(x_2)\\ {\phi }_0(x_3)& {\phi }_1(x_3)& {\phi }_2(x_3)\\ {\phi }_0(x_4)& {\phi }_1(x_4)& {\phi }_2(x_4)\\ {\phi }_0(x_5)& {\phi }_1(x_5)& {\phi }_2(x_5)\\ {\phi }_0(x_6)& {\phi }_1(x_6)& {\phi }_2(x_6)\end{array}\right)=\left(\begin{array}{ccc}1& 1& 1\\ 1& 1.10517& 0.90484\\ 1& 1.22140& 0.81873\\ 1& 1.34986& 0.74082\\ 1& 1.49182& 0.67032\\ 1& 1.64872& 0.60653\\ 1& 1.82212& 0.54881\end{array}\right)$$
  ③ 写出 $y$ 向量：
$$y=\left(\begin{array}{c}2\\ 2.20254\\ 2.40715\\ 2.61592\\ 2.83096\\ 3.05448\\ 3.28876\end{array}\right)$$
  ④ 解法方程组：

$$G^{T}Ga=G^{T}y$$
  得到：$a_0=1.98614a_1=1.01700a_2=-1.00304$ 故所求的拟合函数为：$y=1.98614+1.01700e^x-1.00304e^x$

---

三、最小二乘法应用（matlab）

1. 自行编写代码实现

  拟合函数：三项偶次多项式 $P_n(x)=a_0+a_2{x}^2+a_3{x}^4$
  matlab代码如下：

%x,y为待拟合得数据，返回值p为拟合函数的系数（按x的升幂排列）
function [p]=polyfit_2(x,y)   
if length(x) ~= length(y)
warning('输入矩阵维度有误');
end
m=length(x);
A=[m sum(x.^2) sum(x.^4) ; sum(x.^2) sum(x.^4) sum(x.^6) ; sum(x.^4) sum(x.^6) sum(x.^8)]; %法方程组系数矩阵
b=[sum(y) ; sum(y.*(x.^2)) ; sum(y.*(x.^4))]; 
p=A\b; %求解法方程组
end

  采用一般形式的最小二乘法 代码更为简洁！：

%x,y为待拟合得数据，返回值p为拟合函数的系数（按x的升幂排列）
function [p]=polyfit_22(x,y)
if length(x) ~= length(y)
warning('输入矩阵维度有误');
end
g0=x.^0; 
g1=x.^2;
g2=x.^4;
G=[g0 g1 g2]; %G矩阵构造
%=====normal equation
A=G'*G; %法方程组的系数矩阵
b=G'*y;
p=A\b;  %求解法方程组
end

（掌握了原理，任何编程语言都可以实现拟合方法，甚至还可以自己写一个属于自己的拟合工具箱！！）

2. 利用Curving Fitting Tools工具箱

  自行编写代码还是太麻烦？其实matlab早为我们考虑了这个问题！利用Curving Fitting Tools帮助我们快速实现拟合。Curving Fitting Tools参考文档：https://www.mathworks.com/help/curvefit/curve-fitting.html?searchHighlight=curving fit&s_tid=srchtitle

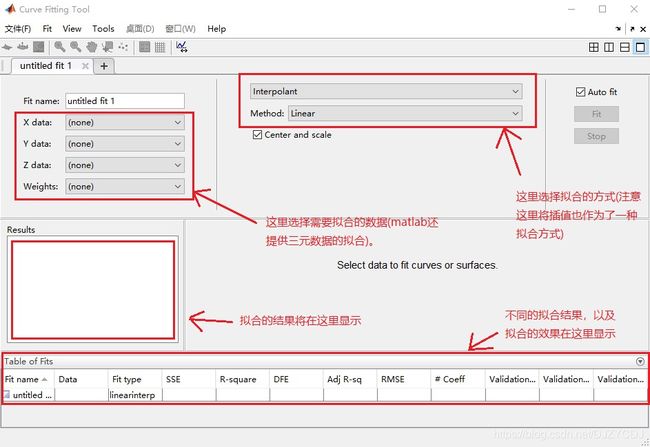
2.1 命令行输入cftool即可打开工具箱

1. 在命令框中输入 cftool 即可打开工具箱
   
   
2. 选定拟合的对象
   
3. 选定拟合函数类
   
   例如选择多项式拟合：
   
4. 工具箱中个参数的含义

SSE(Sum Squared Residual)：残差平方和，越接近0，表示与数据拟合的越好，但是要小心过拟合；
R-Square：确定系数，$R-Square={\sum }_{i=1}^n(y-y_i{)}^2/{\sum }_{i=1}^n(y-y_i{)}^2$，趋近于1较好
DFE：误差项自由度
RMSE(Root Mean Squared Error)：均方根误差
#Coeff：模型的系数数量（非自定义模型时出现），相近拟合效果选择数量少的，防止过拟合。

2.2 拟合结果的调用

2.2.1生成代码(Generate Code)

  有些时候我们不仅需要拟合的图像，还需要拟合的结果。利用Curving Fitting Tools 得到的拟合模型可以直接生成代码非常方便！
点击窗口左上角：文件(Files)—> Generate Code

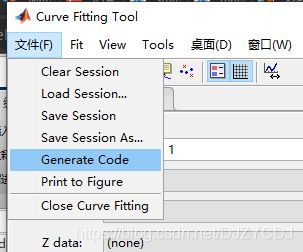
自动生成的函数保存下来，就可以直接调用了

2.2.2调用函数

创建脚本test 测试自动生成的函数

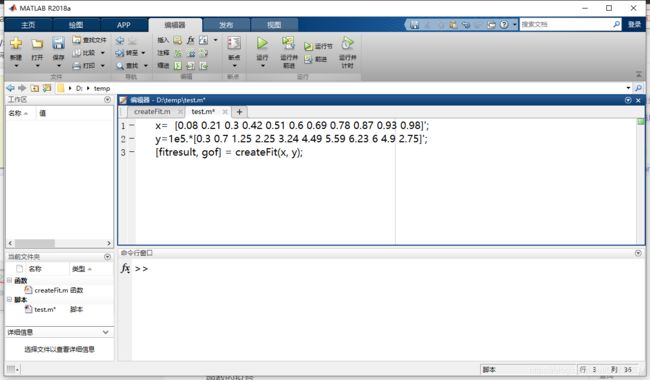
matlab默认为我们绘制了一幅图，同时返回了两个对象：fitresult 和 gof

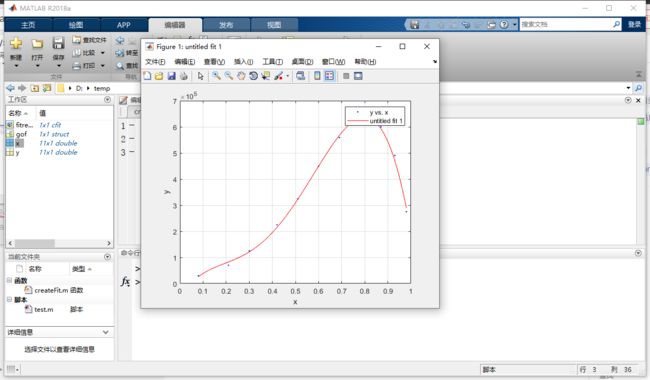
2.2.3返回值fitresult 和 gof 的调用

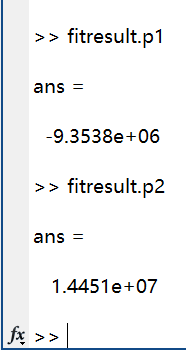
① 直接将fitresult作为函数，可按照拟合公式返回数值解。

② fitresult.相关参数，返回相关拟合参数。

---

如有问题，欢迎讨论