Deep GSP ： 面向多目标优化的工业界广告智能拍卖机制

丨目录：

   · 背景

   · 问题定义

    ·  Deep GSP

   · 实验

   · 与现有学术界和工业界类似方案的差异

   · 展望

   · 关于我们

   · 参考文献

▐ 背景

广告拍卖机制是对竞争性资源的一种高效的市场化分配方式。电商广告中的拍卖机制设计（Mechanism Design in Online E-commerce Advertising），旨在从平台视角出发制定拍卖策略，通过“流量分配” 和“扣费”两个抓⼿，引导广告主有序竞争，并使得流量博弈趋向优化广告主、平台、媒体多方利益。

信息流广告全面进入重用户体验的时代，广告分配机制也需要兼顾广告主诉求、用户体验、广告消耗等多个目标的影响，平台机制不仅需要对收入负责，还需要对整个竞价系统的长期健康稳定负责。这一问题不同于经典的多目标优化问题或拍卖机制问题的研究：

• 动态博弈环境下的目标优化。在线电商广告系统中，不同利益方之间的优化诉求可能存在冲突（例如平台收入和用户体验），且不同利益方均具有理性心智，在一个博弈环境下进行动态交互，这不同于传统的静态多目标优化问题。

• 面向多目标的拍卖机制设计。传统的机制设计方法往往只考虑优化平台的收入或社会福利（social welfare，平台收入和广告主的预期收益），极少同时考虑其他多个指标（例如点击、转化、收藏加购、客户体验等指标）。

因此我们需要考虑在多利益方的动态博弈场景下建模并优化多个目标。

▐ 问题定义

我们定义电商广告场景下，多利益方（广告主、用户、平台）博弈背景下的多诉求指标优化问题（Multiple Stakeholders' Ad Performance Objectives Optimization in the Competitive E-commerce Advertising）：

402 Payment Required

其中表示要优化的机制（即分配和扣费规则）；代表各利益方的诉求指标集合，如：平台收入、点击、转化、收藏加购、成交量等等，所有诉求指标通过预先给定的重要性权重求得聚合目标函数。同时，在优化过程中需要满足两个关于机制属性的约束：

• 博弈均衡约束（Game Equilibriium Contraints）：所有广告主（竞价者）在当前机制下能够达到博弈均衡状态，在当前状态下广告主对分配结果感到满意（即分配结果的改变不能使广告主的收益变多）。在算法博弈论（Algorithmic Game Theory）领域，有一些和拍卖机制相关的博弈均衡概念。例如经典的Myerson定理证明了：如果一个机制在单坑拍卖场景中是单调分配（Monotone Allocation），且扣费为保持当前分配下的最小出价（critical bid based pricing），那么这个机制是激励兼容（Incentive-Compatible, IC）[1] 的：

THEOREM 1 (Single Slot Incencentive-Compatible)[1]. A single slot auction mechanism is  incentive-compatible if and only if the allocation scheme is monotone, i.e., the winning bidder would still win the auction if she reports a higher bid, and the pricing rule is based on the critical bid, which is the minimum bid that the winning bidder needs to report to maintain the winning state:

402 Payment Required

402 Payment Required

而对于多坑拍卖（multi-slot auction），我们考虑对称纳什均衡（Symmetric Nash Equilibrium, SNE）[2]：

THEOREM 2 (Multi-Slot Symmetric Nash Equilibrium)[2] An auction mechanism satisfies symmetric Nash equilibrium (SNE) if and only if each bidder in this equilibrium prefer her current allocated slot to any other slot :

where is the inherent click-through rate of the slot .

它表示每个广告主在平台分配给的坑位下utility最大，不会嫉妒其他坑位。

• 机制的平滑切换约束（Smooth Transition Contraints）。在线广告系统的动态性很强，不同利益方在不同时刻的优化诉求也不尽相同，当机制从服务于一个目标切换到另一目标时，应该保证各方利益指标平稳过渡，即机制的平滑切换。可以用如下公式表示：

其中表示一个benchmark机制，表示广告主utility的一个下界，即机制在优化过程中不应低于这个下界。

解决这一问题有两个难点：（1）许多优化诉求指标难以精确估计（例如成交额、商品收藏加购量等），无法得到精确的解析形式，只能通过真实反馈的方式才能获得。此外，不同阶段的优化目标可能不一样（例如大促期间平台机制更倾向于成交，而日常期间更倾向于消耗），如何以一种更灵活的优化方式给予平台机制更强的调控能力。（2）需要一种简洁的数学形式表达机制需要满足的属性（博弈均衡/平滑切换），并将其融入到机制的优化过程中。对于传统的GSP机制，尽管一些博弈论方面的理论工作已经证明GSP在博弈均衡方面有较好的保障，但GSP仅能优化平台收入，无法对任意给定的多诉求指标进行优化；而对于工业界比较常用的uGSP机制，其对各诉求指标的预估值（例如pctr/pcvr等）较为依赖，很难根据流量波动和预估不精准做动态调整，缺乏直接对标终局效果的自适应调控能力。

我们通过引入深度神经网络的参数化模型和基于后验真实反馈的端到端策略优化来求解第一个问题，通过传统机制在博弈均衡性质上的一些先验知识并融入到模型的损失函数来解决第二个难点。

▐ Deep GSP：面向多目标优化的工业界广告智能拍卖机制

我们提出一种面向多目标优化的广告智能拍卖机制Deep GSP（Deep GSP Mechanism）。Deep GSP在传统GSP机制的基础上通过引入深度神经网络来提升其分配能力，并通过强化学习朝着提升给定的多利益方目标的方向直接优化这一策略模型的参数；在扣费上Deep GSP延续GSP的二价计费，模型的优化在满足机制激励兼容/机制平滑切换的条件下进行。不同于GSP/uGSP等机制在计算rank score时严重依赖预估值，Deep GSP机制的优化过程是基于真实反馈进行的，因此也可以支撑任意定制目标的优化，是一种基于数据驱动的学习方法。

机制设计

Deep GSP使用基于深度神经网络的rank score function代替传统GSP机制中的Ecpm排序。将广告主出价、广告特征、用户信息、广告主营偏好等作为特征，映射到一个连续实数值空间，表示这一请求下这一广告的rank score。我们用符号表示神经网络计算出的第个广告的rank score。而如何将机制的desirable properties与深度学习模型的端到端训练进行融合是Deep GSP的核心问题：

博弈均衡约束（Game Equilibriium Contraints）

为了满足机制的博弈均衡性，深度排序分函数应该满足在出价这一维特征上的单调性，即广告主提升其出价不会拿到更差的流量分配结果；与此同时，其扣费应为拿到其分配结果所应给出的最小报价（即最小扣费原则）。这要求深度排序分函数同时具有单调性和可以求逆的特性，我们提出“单点单调损失”和“近似可逆扣费”来实现：

（1）单点单调损失（Point-wise Monotonocity Loss，PML）

不失一般性，我们将深度排序分函数形式化如下，表示出价和深度模型输出的乘积：

为了保证单调分配，在上的偏导数应大于等于0，则可以设置单点单调损失函数如下：

402 Payment Required

该损失函数是一种基于数据驱动的方法来计算单调性损失，即当排序分函数的输出在出价这一维特征的导数小于0时，在模型训练中施加一个惩罚。

（2）近似可逆扣费（Approximate Inverse Operation, AIO）

可逆扣费的计算可以近似如下：

在离线的实验中我们观察到rankscore模型在加入PWL后其单调性可以基本得到保障（如下图），近似扣费解和离线计算的真实值之间的差异也较小（Table2中的PER值，表示近似值与二分查找计算出的真实值之间的比值）。

机制的平滑切换约束（Smooth Transition Contraints）

进一步，在明确了模型的定义和博弈均衡约束的具体实现后，我们设计具体的模型优化方法，并将平滑切换的机制特性作为约束融入其中。由于真实反馈信号的链路很长且不可解析（比如收藏加购量、成交量等），而预估模型也往往存在估计偏差（例如点击率、转化率预估模型），我们将Deep GSP的深度排序分模型的优化建模成一个决策问题，并使用基于真实反馈的model-free RL进行优化。排序分策略的状态即上文介绍过的输入特征；动作为排序分数。奖赏函数包含两部分：一部分为优化目标，即加权聚合的多诉求指标；另一部分通过使用多目标优化中常用的技术来衡量机制改变后对广告主utility的波动，从而实现平滑切换：

402 Payment Required

机制实现

如前面介绍，在真实电商广告的场景中，许多优化诉求指标难以得到精确的可解析形式（例如商品收藏加购量等），且只能通过真实反馈的方式才能获得。这一特点与强化学习中的探索过程比较类似，因此我们将机制分配模型的学习建模成一个策略学习问题（Policy Optimization），并使用深度强化学习来优化其参数。我们定义这一决策问题的几个要素：

• 状态：广告主对流量的出价、广告特征（类别、点击率预估值、转化率预估值等）、用户特征（性别、年龄、收入等）以及广告主信息（预算、营销倾向等）以及一些其他上下文信息（场景、session内全局统计信息等等）。

• 动作：每个广告的rankscore。

• 奖励：每个广告在场景中曝光后的多目标加权聚合值（需经过量纲统一处理）。

• 状态转移：在当前的版本下，Deep GSP暂时不考虑机制分配策略的长期价值（即episode_length=1），当然这是未来值得探索的一个方向。

我们使用深度强化学习中一种经典的连续控制学习算法，深度确定性策略梯度（Deep Deterministic Policy Gradient）来实现模型优化。具体地，设计一个值函数（）和一个策略函数（），策略函数（）即要优化的深度rankscore模型，值函数（）来评估一组 [状态,动作] 对的价值（使用奖励函数拟合），并通过路径梯度求导来指导策略函数的训练。两个模型的具体优化方法如下：

402 Payment Required

整个Deep GSP的训练流程与真实反馈的交互过程如下图所示：

  Deep GSP机制在部署后的执行流程如下：

• 分配：候选广告集合中的所有广告根据网络输出的rankscore进行排序（倒排），排在前位（即具体场景中需要展现的广告数量）的广告胜出并展现。

• 扣费：每一个胜出广告根据其下一位广告的排序分通过深度打分函数求逆（即近似可逆扣费方案）计算其相应的扣费。

Deep GSP能够根据真实的多目标反馈信号进行端到端的优化，克服诉求指标难以建模预估的不足，而且对真实在线广告系统的动态波动具有较好的鲁棒性。

▐ 实验

多目标优化能力&机制性质保证

为了能够充分验证Deep GSP在优化多目标上的表现，以及机制内在机理，我们在离线设计实验对这些进行充分的分析。

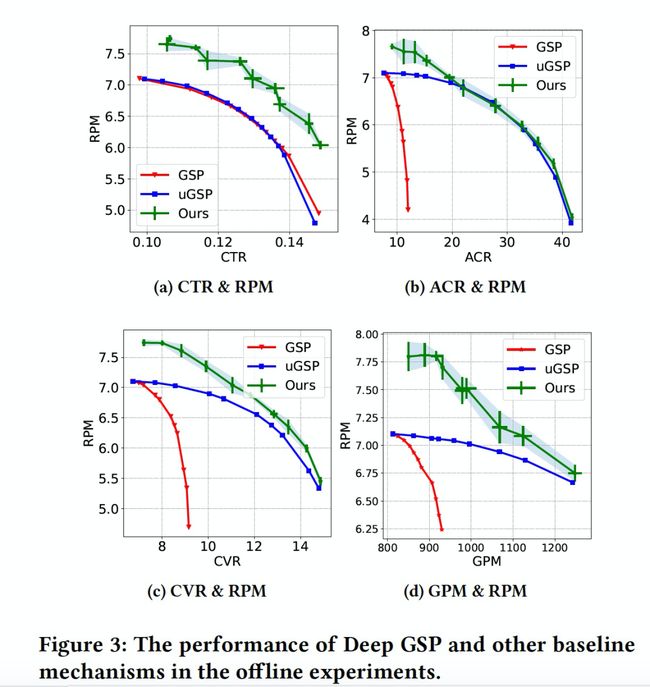
首先在离线侧我们基于XRL强化学习平台搭建了一个模拟器，并利用点击率、转化率、收藏加购率等指标的分场景校准值来模拟真实反馈。下图分别展示了四项实验的优化指标对比：RPM/CTR、RPM/ACR、RPM/CVR、RPM/GPM。我们发现相比于GSP和uGSP，Deep GSP能在各个指标上优化的更充分，尤其是在其他指标持平的情况下能够显著提升收入，体现出了深度模型的优化能力。

下表展示了在不同优化诉求场景下的有关博弈均衡设计的指标。其中单调性指标（表示rank score排序与其对应的bid在排序上的一致性，使用spearman相关系数计算来实现）、扣费时引入的逆计算误差指标（表示近似扣费与离线通过二分搜索计算出的真实扣费之间的比值）均与理想值1较为接近，证明了PML和AIO的误差较小。Table 2中最后一列IC表示通过拍卖日志数据离线计算出的激励兼容指标（Data-driven IC [3]），其值越接近于1表示机制越趋近于激励兼容。

最后我们验证了机制的“平滑切换”功能。下图展示了当机制目标从“CTR”切换至“RPM”时，广告主Utility的变化，可以发现广告主效果会随着参数的提升呈缓慢下降趋势，而非剧烈震荡。

▐ 与现有学术界和工业界类似方案的差异

在学术界已有一些研究工作focus在深度学习和机制设计的结合。例如ICML19中的工作 [4]提出了端到端的分配网络和计费网络RegretNet，并将机制的IC约束融入到网络结构的设计或优化的loss当中。RMD用提出了基于强化学习的拍卖机制来优化收入等。但这其中大部分的研究还是在经典拍卖场景中，其数据来自于模拟的bidder value distribution，和真实广告拍卖场景中的数据分布差异较大。在优化多方利益这个问题上，现在工业界也有一些通过业务经验事先设定排序公式，并通过深度学习（或强化学习）来预测（或优化）每条流量中的参数，得到流量维度的“个性化排序公式”，以实现在不同的流量优化不同的指标，并做到所有流量指标的提升，上述的算法在各自的业务中都取得了显著的效果提升。

从技术本质上来看，这些工作都是因为在广告场景中，多方利益需要协同优化，实际场景复杂，传统的GSP/UGSP拍卖机制已无法更好的实现动态博弈场景下的效果最优，进而寻求一种新的拍卖机制来解决解决工业场景上面向真实效果优化。但拍卖机制的设计不是单纯的优化问题，还需要考虑广告主的理性行为，即因为机制的变化而导致广告主策略行为的变化，并可能进一步导致优化效果的变化。个性化排序公式是解决这个问题的一个途径，在拍卖机制设计上可以沿用GSP框架从而省去对机制性质的深究。但同时这种实现方式由于事先确定了分配函数的参数化形式，使得其在扩充特征空间或优化更多样目标时可能受到可扩展性的限制。Deep GSP正是在这样的背景下，从拍卖机制设计的本质出发，将模型学习和拍卖机制深度融合，建模多利益方的“动态博弈”场景，并面向后验任意多目标来进行优化，同时将机制性质融合在神经网络的优化过程中，充分释放模型优化多目标的能力。Deep GSP相关工作论文发表在WSDM 2021，感兴趣同学也可以查阅原文了解更多。

论文下载：https://arxiv.org/abs/2012.02930

▐ 展望

Deep GSP是阿里妈妈展示广告机制策略团队将“拍卖机制”与“端到端学习”结合的一次尝试，在后续的工作中，我们也在继续“模型算法优化+机制博弈约束”这种“一体两面”的研究思路，在算法设计方面提高建模能力和优化能力；在理论方面，研究learning-based机制的激励兼容性，探究如何将其更好的融入算法设计中，并进一步尝试在机制的可解释性上有所突破。

▐ 关于我们

我们是阿里妈妈展示广告机制策略算法团队，致力于不断优化阿里展示广告技术体系，驱动业务增长，推动技术持续创新；我们不断升级工程架构以支撑阿里妈妈展示广告业务稳健&高效迭代，深挖商业化价值并优化广告主投放效果，孵化创新产品和创新商业化模式，优化广告生态健壮性；我们驱动机制升级，并已迈入 Deep Learning for Mechanisms 时代，团队创新工作发表于 KDD、WWW、ICML、CIKM、WSDM、AAMAS、AAAI 等领域知名会议。在此真诚欢迎有ML背景的同学加入我们！

投递简历邮箱（请注明-展示广告机制策略）：

[email protected]

参考文献：

[1] Myerson, R. B. (1981). Optimal auction design. Mathematics of operations research, 6(1), 58-73.

[2] Varian, H. R. (2007). Position auctions. international Journal of industrial Organization, 25(6), 1163-1178.

[3] Yuan Deng, Sébastien Lahaie, Vahab Mirrokni, and Song Zuo. 2020. A data-driven metric of incentive compatibility. In Proceedings of The Web Conference 2020. 1796–1806.

[4] Dütting, P., Feng, Z., Narasimhan, H., Parkes, D., & Ravindranath, S. S. (2019, May). Optimal auctions through deep learning. In International Conference on Machine Learning (pp. 1706-1715). PMLR.

[5] Tacchetti, A., Strouse, D. J., Garnelo, M., Graepel, T., & Bachrach, Y. (2019). A neural architecture for designing truthful and efficient auctions. arXiv preprint arXiv:1907.05181.

[6] Shen, W., Tang, P., & Zuo, S. (2019, May). Automated mechanism design via neural networks. In Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems (pp. 215-223).

END

也许你还想看

丨KDD2021 | USCB:展示广告约束出价问题的通用解决方案

丨KDD 2021 | Neural Auction: 电商广告中的端到端机制优化方法

丨WSDM 2022 | 一种用于在线广告自动竞价的协作竞争多智能体框架

欢迎关注「阿里妈妈技术」，了解更多~

疯狂暗示↓↓↓↓↓↓↓