曲线拟合——最小二乘法（ Ordinary Least Square，OLS）

---

前言

随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习最基础的内容：最小二乘法。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、曲线拟合是什么？

曲线拟合也就是求一条曲线,使数据点均在离此曲线的上方或下方不远处, 它既能反映数据的总体分布,又不至于出现局部较大的波动, 能反映被逼近函数的特性,使求得的逼近函数与已知函数从总体上来说其偏差按某种方法度量达到最小。
设函数y=f(x)在m个互异点的观测数据为

求一个简单的近似函数φ(x)，使之“最好”地逼近f(x),而不必满足插值原则。这时没必要取φ(xi) = yi, 而要使 i=φ (xi)yi 总体上尽可能地小。这种构造近似函数 的方法称为曲线拟合,称函数y=φ(x)为经验公式或拟合曲线。
如下为一个曲线拟合示意图。
清楚什么是曲线拟合之后，我们还需要了解一个概念—— 残差。
曲线拟合不要求近似曲线严格过所有的数据点，但使求得的逼近函数与已知函数从总体上来说其偏差按某种方法度量达到总体上尽可能地小。若令（1-1）
则为残向量（残差）。
“使 （1-1） 尽可能地小”有不同的准则
（1）残差最大值最小
（2）残差绝对值和最小（绝对值的计算比较麻烦）
（3）残差平方和最小（即最小二乘原则。计算比较方便，对异常值非常敏感，并且得到的估计量具有优良特性。）

二、最小二乘法是什么？

个人粗俗理解：按照最小二乘原则选取拟合曲线的方法,称为最小二乘法。
百度百科：最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

三、求解最小二乘法（包含数学推导过程）

我们以最简单的线性模型来解释最小二乘法。什么是线性模型呢？

监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，n个自变量，且因变量和自变量之间是线性关系，则称为一/多元线性回归分析。
如何求解最小二乘问题？（使用极小值原理）
　首先应确定函数类（原则:根据实际问题与所给数据点的变化规律），在实际问题中如何选择基函数是一个复杂的问题，一般要根据问题本身的性质来决定。通常可取的基函数有多项式、三角函数、指数函数、样条函数等。我们以二元线性方程为例进行数学推导，如下：
　

四、使用步骤

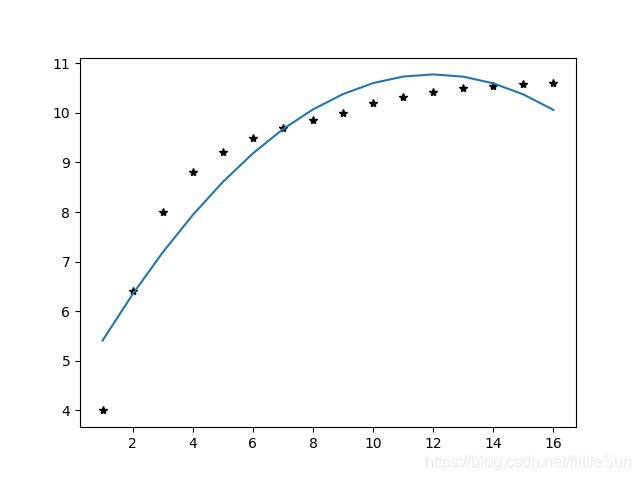
例:在某化学反应里，测得生成物浓度y（%）与时间t（min）的数据见表3-3，试用最小二乘法建立t与y之间的经验公式。

1.引入库

代码如下（示例）：

import numpy as np
import matplotlib.pyplot as plt
import numpy.linalg as lg

2.读入数据

代码如下（示例）：

t=np.arange(1,17,1)
y=np.array([4,6.4,8,8.8,9.22,9.5,9.7,9.86,10,10.20,10.32,10.42,10.5,10.55,10.58,10.6
])
plt.figure()
plt.plot(t,y,'k*')
# y=at^2+bt+c

A=np.c_[t**2,t,np.ones(t.shape)]

w=lg.inv(A.T.dot(A)).dot(A.T).dot(y)

plt.plot(t,w[0]*t**2+w[1]*t+w[2])
plt.show()

总结

以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。