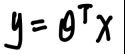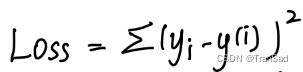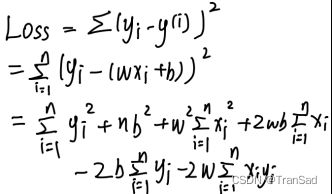最小二乘法理解与应用

  最小二乘法是一个既熟悉又陌生的东西。

  在回归问题中我们经常使用最小二乘法来预测出一条直线或者曲线用于拟合真正的数据点。而拟合数据的方式就是使用最小二乘法——使我们的预测值与真实值之间的差的平方和最小。

  因为看起来十分基础和简单，甚至用上面这一段话就讲完了。

  然而，为什么是平方和呢?而不是一次方或者三次方?因为一次方会有正负，无法表示实际距离？那么带上绝对值不就行了嘛……原来我对这个问题没有仔细想过，感觉最小二乘法反正就是最常用最经典的方式罢了，类似于求个欧氏距离嘛大家都很喜欢用的一种表示方法而已。

  但实际上，可以从概率统计学的角度探索最小二乘法的由来，从而证明其合理性。

最小二乘法由来：

  假设我们现在有很多样本点(x1,y1),(x2,y2),(x3,y3)……(xi,yi)，我们希望预测出一条直线：

y=wx+b来拟合这些样本点。

  一步一步来，首先这个b是截距，带着它后面会看起来很麻烦，机器学习中常用的方式其实是在x中添加一个常数项1，然后把b“添加”到w中，这样直线就可以写成：

  这里的θ比原来的w多了一个b，x也比原来的x多了一个1，乘起来的话就会多出一个1*b就是原来的截距了。

  那么对于每一个样本点，我们的预测值y(i)为：

  已知xi对应的实际值为yi,假设误差yi-y(i)为εi，接下来我们就从这个误差项εi展开分析：

  现在我们有：

  首先得明确：每个数据点都有一个误差项εi,且这些误差项服从标准正态分布（均值为0标准差σ）。因此带入正态分布公式，我们有：

  从条件概率的角度出发，我们希望在xi和θ组合的情况下yi发生的概率最大——是不是非常耳熟，这就是要开始用似然函数了。（关于似然函数原来整理过一篇）

  我们把每一个样本点都考虑进来（让他们进行累乘），就可以得到似然函数为：

  我们现在希望找到一个合适的θ值使得这个式子最大，解法很简单，用常用的取对数方法，就可以得到：

  让这个式子最大，除去一个常数项，等价于让下面式子最小：

  这样就得到了我们熟悉的最小二乘法了。

最小二乘法应用

还是对于在二维平面当中拟合直线这个例子，我们已经确定了使用最小二乘法，则目标函数为：

 

  设直线格式为y=wx+b，展开得：

联立，可求解得到答案：

  这样一来，我们几乎就可以得到在二维平面拟合直线的结论性答案了。

  现在来一个简单的具体例子：

  在二维平面中，有三个点，值分别如下：(1,1),(2,2),(3,4)，现在要求预测出一条直线来拟合这些数据点。

（为什么是三个点呢？因为一个点没有任何意义，两个点确定一条直线，当三个点的时候，我们才需要用最小二乘法来拟合，所以至少选三个点。）

  直接用算出来的结论，可知：

w = [3*(1*1+2*2+3*4)-(1+2+3)(1+2+4)]/[3*(1*1+2*2+3*3)-(1+2+3)*(1+2+3)]  = 3/2

b = (1+2+4)/3-3/2*(1+2+3)/3  = -2/3

  所以可拟合出直线：y=3/2x-2/3，将x=1,2,3带入验算，可以发现拟合的效果真的还是不错的。

  上面只是比较简单的应用场景，我们可以直接使用一个看似不是很复杂的结论。类似的，我们还可以通过最小二乘法去拟合二次曲线（此时我们不再设f(x)=wx+b,而是y=w*x的平方+b*x的一次方+c，然后分别对w，b，c求偏导再解方程即可）——也就是说，我们可以选择不同的f(x)类型，通过最小二乘法得到不一样的拟合曲线。（当然，但当情况复杂之后，我们就很难通过解方程来得到一个实际的答案了， 此时我们更多的是采用梯度下降的方式去直接地优化和逼近结果。）

  小结一下，这篇文章主要梳理了一下最小二乘法的由来以及计算与应用，也用来方便以后温故而知新~