零样本学习—Learning to detect unseen object classes by between-class attribute

零样本学习

算法概要

前提

$$(x_1,l_1),\cdots (x_n,l_n)为训练样本x和相应类别标签l.这样的成对数据共有n组，l中一共有k类，$$
用$$Y=y_1,y_2,...,y_k$$表示，Z = {$z_1,...,z_l$}为测试集所包含的L个类别，这里的$Y和Z$分别为可见类和不可见类，二者之间没有交集。

目标

学习一个分类器 f: X$\to$ Z, 也就是通过学习分类器，找到训练数据$x$和相应的可见类别标签$l$,与位置类别标签$Z$之间的关系。

思路

通过建立一个人工定义的属性层$A$,这个属性层是高维的，可以表征训练样本的各项特征，比如：颜色、条纹等。目的是将基于图片的低维特征分类器转化到一个表征高维语义的特征的属性层，这样使得分类器分类能力更广，具备突破类别边界的可能。
基于这个思路，作者提出了两个方法：DAP和IAP。

具体原理

DAP

DAP在样本和训练类别标签之间加入了一个属性层A，a为M维属性向量$(a_1,a_2,...,a_M)$ 每一维度代表一个属性，且在$0,1$之间取值，对于每个标签都对应一个M维向量，作为其属性向量（原型），通过训练集$X$对应属性进行训练，学习得到属性层参数$\beta$,之后便可以得到$P(a|x)$,将输入测试实例x输出的标签，作为待估计参数，对于测试实例$x$,即可利用MAP思想，找出概率最大类为输出的估计类。

$Z的后验概率为：$
$$P(z|x)=\sum _{a\in (0,1)M}p(z|a)p(a|x)$$

根据贝叶斯公式：
$$=\sum _{a\in (0,1)M}\frac{p(a|z)p(z)}{p(a)}p(a|x)$$

根据文章中的假设各个维度的属性条件独立，公式可以表示为：
$$\sum _{a\in (0,1)M}\frac{p(a|z)p(z)}{p(a)}\prod _{m=1}^{M}p(a_m|x)$$

右DAP的图模型，知$p(a^z)=p(a)$ 可得到：

整理得到：

省略掉为零的项：

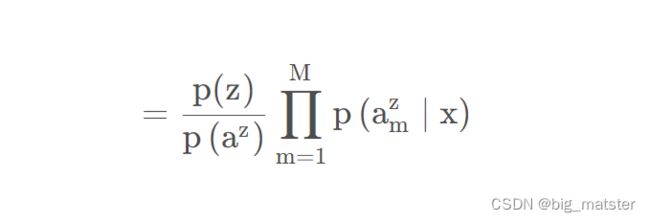
根据属性之间独立：

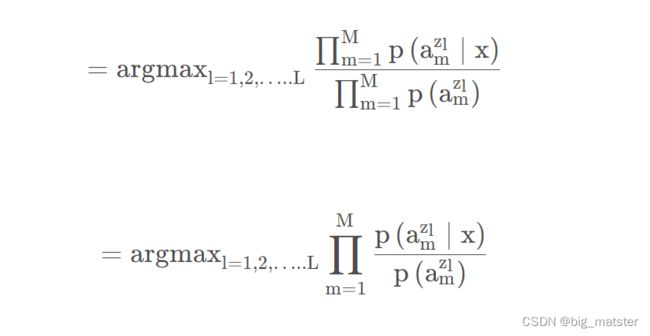
$f(x)$的输出即为对于输入x的预测标签。

IAP

区别于DAP，DAP的PGM中属性层是在实例层和标签层（包括可见和不可见）之间，而IAP则是将属性层置于可见标签层与不可见标签层之间，用来迁移可见类标签与实例的信息到不可见标签层。

此时的后验概率为:
$$p(a_m|x)=\sum _{i=1}^{k}p(a_m|y_k)p(y_k|x)$$

学习心得

慢慢地将各种零学习啥的都全部给其搞彻底，研究透彻！
真心的羞涩难懂，慢慢地将各种东西都研究透彻，真心艰难的理由与打算。全部将其搞定都行啦的回事与样子。