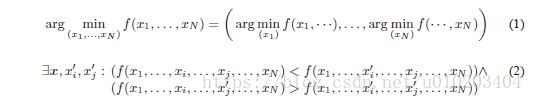使用基于变量交互学习的合作协同进化的大规模全局优化

引用

LaTex

@inproceedings{Chen:2010:LGO:1887255.1887289,
author = {Chen, Wenxiang and Weise, Thomas and Yang, Zhenyu and Tang, Ke},
title = {Large-scale Global Optimization Using Cooperative Coevolution with Variable Interaction Learning},
booktitle = {Proceedings of the 11th International Conference on Parallel Problem Solving from Nature: Part II},
series = {PPSN’10},
year = {2010},
isbn = {3-642-15870-6, 978-3-642-15870-4},
location = {Kraków, Poland},
pages = {300–309},
numpages = {10},
url = {http://dl.acm.org/citation.cfm?id=1887255.1887289},
acmid = {1887289},
publisher = {Springer-Verlag},
address = {Berlin, Heidelberg},
keywords = {cooperative coevolution, incremental group strategy, large-scale optimization, numerical optimization, variable interaction learning},
}

Normal

W. Chen, T. Weise, Z. Yang, and K. Tang, “Large-scale global optimization using cooperative coevolution with variable interaction learning,” in International Conference on Parallel Problem Solving from Nature, 2010, pp. 300–309.

---

主要内容

CC 合作协同进化 Cooperative Coevolution

1. 非交互变量 — 同一组
2. 交互变量 — 可分

早期研究：

1. 单维
2. 对半分

组的大小不一 应该考虑

大规模优化测试集

---

###维度灾难 Curse of Dimensionality

传统算法 解决大规模问题时，性能急剧降低。

CC策略 分而治之： CC 将搜索空间分为低维子空间；将决策变量分为变量组

问题的分解策略需要考虑

本文提出了一种泛化的可拓展的高效方法

---

合作协同进化 CC

基本组成：

1. 分解方法
2. 合作：每个子种群选出代表元素
3. 每组的变量使用优化算子进行优化

每个子种群的优化为一个phase。

所有组的一次迭代优化为一个cycle。

算法1和2中，问题被看作是完全可分的。

---

发现决策变量关系

分解策略是CC最重要的组成部分

若函数$f$满足式（1），即，可以通过相继地沿着各个坐标轴进行线性搜索得到全局最优。

（2）式中，变量$i$和$j$是有交互作用的。

在CC中，决策变量可以分解成多组：$G_1,G_2,\dots ,G_m$，等价于：适应函数$f$能够通过分量函数$f_1,f_2,\dots ,f_m$的线性组合进行估计。

文献【1】中提出了一个简单方法：每个变量的最优值组成$best$向量；在种群$popcc$中，最优个体为$new$，即只改变维度$i$；还有一个随机候选个体$rand$。

由此生成以上两个候选个体，以判断变量$i$和$k$是否依赖。$x$中的$k$来自于最优个体$best$，故其优于$k^{\prime }$（来自于随机生成），因此，$f\left(x\right)\le f\left(x^{\prime }\right)$对于可分变量成立，然而，若$f\left(x\right)>f\left(x^{\prime }\right)$，则变量$i$和$k$是相互作用的。

---

相关工作

早期时：单维或对半分
未考虑变量之间的交互作用

多级金字塔遗传算法【2】
随机分组策略的合作协同进化（DECC-G）【3】
多级合作协同进化（MLCC）【4】

---

CCVIL

提出的CCVIL
Cooperative Coevolution with Variable Interaction Learning
变量交互学习的合作协同进化

首先将所有变量看做是独立的，并分别放到一组；通过迭代，能够发现它们之间的关系，相应地把组融合。

学习阶段

按维进行优化，类似算法2。但是，在每个学习cycle开始前，维度的访问顺序被打乱，每两个维度有相同的概率能够被连续访问。

从随机的角度来看，在一个$N$维问题中，在一次随机排列中，任两个维度相邻的概率为$2/N$。因此，在$K$次学习cycle中，此种情况至少发生一次的概率$p_{capt}$为

算法中的种群大小与内部优化算子代数限制分别设为了3与1。CCVIL在每一个cycle进行了独立的restart操作，以免丢失种群多样性。

设置了学习cycle的上界与下界：$\hat{K}$和$\check{K}$。若在学习阶段的前$\check{K}$个cycle中，不能检测到任何变量交互作用，问题视作是完全可分的，或者存在的交互作用很弱，并转入优化阶段。在$\hat{K}$个cycle后，即使有交互作用没有检测出来，也强制转入优化阶段。推荐设置为$\check{K}=10$与达到$p_{capt}\left(\hat{K}\right)$时的$\hat{K}$。然而，$\hat{K}$不能使学习阶段占用超过60%的FEs。

优化阶段

使用的优化算子为JADE。代数与组的大小有关：$Ge{n}_i=\min \left\{\left|G_i\right|+5500\right\}$。种群大小基于自适应策略：初始为$NP_i = \left| G_i \right| + 10 $；在种群丢失多样性而不能提升时，种群大小变为之前的三倍，并进行独立重启，如【5】，判定条件为$\left( f_{K-1} - f_{K} \right) / f_K < 10^{-2} $。

不同组的优化难度可能不同，若5次cycle都没有提升，认为组已收敛，停止优化。

---

实验研究

设置

1000维问题

所比较的算法为：CCVIL、DECC-G、MLCC与JADE【6】。

3000000的FEs

种群规模：JADE-1000，DECC-G与MLCC为默认值

25次运行。

基准函数与学得的组

函数介绍在文献【7】。

Ackley’s function是可分的，但不是加性可分【8】。
Rosenbrock’s function虽然是完全不可分的，但相互作用很微弱。

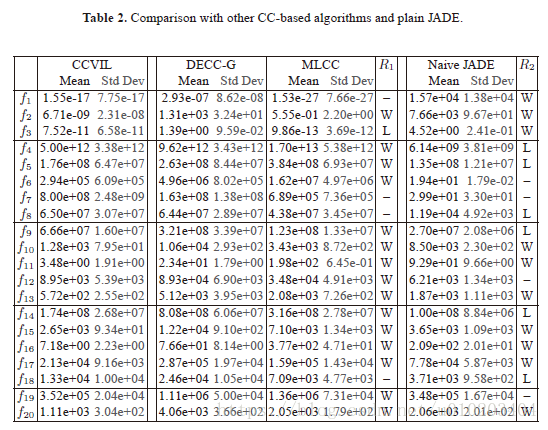
优化效果比较

5%显著级别的双尾Mann-Whitney U 检验
$W$—统计上的明显好于（win）
$L$—失败（loss）
“-”—无明显差异

学习阶段应设置的FEs还应进一步研究。
在学习阶段，是随机打乱变量顺序的。
CMA-ES【9】是更高效的优化算子。

---

---

---

参考文献

【1】 Weicker, K.,Weicker, N.: On the improvement of coevolutionary optimizers by learning variable
interdependencies. In: Proc. 1999 Congress on Evolutionary Computation (CEC’99).
IEEE Press. (1999) 1627–1632
【2】 Aickelin, U.: A Pyramidal Evolutionary Algorithm with Different Inter-Agent Partnering
Strategies for Scheduling Problems. In: GECCO Late-Breaking Papers. 1–8
【3】 Yang, Z., Tang, K., Yao, X.: Large scale evolutionary optimization using cooperative coevolution.
Information Sciences 178(15) (2008) 2985–2999
【4】 Yang, Z., Tang, K., Yao, X.: Multilevel cooperative coevolution for large scale optimization.
In: IEEE Congress on Evolutionary Computation, IEEE Press (2008) 1663–1670
【5】 Auger, A., Hansen, N.: A restart CMA evolution strategy with increasing population size.
In: IEEE Congress on Evolutionary Computation. Volume 2., IEEE Press (2005)
【6】 Zhang, J., Sanderson, A.C.: JADE: adaptive differential evolution with optional external
archive. IEEE Transactions on Evolutionary Computation 13(5) (2009) 945–958
【7】 Tang, K., Li, X., Suganthan, P.N., Yang, Z., Weise, T.: Benchmark functions for the
CEC’2010 special session and competition on large scale global optimization. TR, NICAL,
USTC, Hefei, Anhui, China (2009) http://nical.ustc.edu.cn/cec10ss.php.
【8】 Streeter, M.: Upper bounds on the time and space complexity of optimizing additively separable
functions. In: Genetic and Evolutionary Computation–GECCO 2004, Springer (2004)
186–197
【9】 Hansen, N.,M¨uller, S.D., Koumoutsakos, P.: Reducing the time complexity of the derandomized
evolution strategy with covariance matrix adaptation (CMA-ES). Evolutionary Computation
11(1) (2003) 1–18