Ranked List Loss for Deep Metric Learning | 阅读笔记

Ranked List Loss for Deep Metric Learning | 阅读笔记

---

这是CVPR2019上一篇度量学习的论文。

摘要

深度度量学习（DML）的目的是学习可以捕获数据点之间语义相似性信息的嵌入。在DML中使用的现有成对或三重损失函数在模型改进时由于大量的平凡对或三元组对而导致收敛缓慢。为了改善这一点，最近提出了基于排序的结构化损失，以结合多个示例并利用其中的结构化信息，它们收敛得更快，并实现了最先进的性能。在此基础上，作者提出现有排序激励结构损失的两种局限性，并提出了一种新的排序列表损失方法来解决这两种问题。首先，首先，给定查询，仅结合一部分数据点以构建相似性结构。因此，忽略了一些有用的示例，并且该结构的信息量较少。为了解决这个问题，提出了通过利用图库中的所有实例来构建基于集合的相似性结构。将样本分为正样本集和负样本集，目标是利用一个margin使查询更接近正样本集，而不是负样本集。其次，先前的方法旨在在嵌入空间中尽可能接近正样本对。结果，类内数据分布可能会被丢弃。相反，本文提出为每个类学习一个超球面，以保留其中的相似性结构。 广泛的实验表明，所提出的方法在三个广泛使用的基准上达到了最先进的性能。

---

Introduction：

深度度量学习（DML）在计算机视觉的各种应用中起着至关重要的作用，例如图像检索、聚类和迁移学习。此外，DML是挑战极端分类设置的一个很好的解决方案，其中存在大量的类，而每个类只有很少的图像。一个经典的应用就是人脸识别，Google的FaceNet模型使用Triplet-Loss刷新了当时人脸识别的记录，在人脸验证方面实现了超越人类的性能。

基于深度学习的度量学习其发展主要体现在各种不同的Loss Function 上。最基本的两种损失函数分别是 Contrastive Loss 和 Triplet-Loss。Contrastive Loss 主要是约束成对数据之间的相似或者不相似。Triplet-Loss 则包括一个锚点(anchor)、一个正样本和一个负样本，它的目的是使得锚点和正样本的距离尽可能小，与负样本的距离尽可能大。一般来说，Triplet-Loss的效果比Contrastive Loss的效果要好，因为他考虑了正负样本与锚点的距离关系。基于上述的两种损失函数衍生出了很多变形，比如将数据丰富的结构化信息加入到Loss中，而不仅仅局限于二元组或三元组。

本文贡献如下：

• 提出了一种新颖的基于排序的结构化损失(RLL)来学习判别式嵌入。与以前的排序思想损失相比，是第一个结合所有非平凡数据点并利用其中结构的人。此外，我们还为每个类学习了一个超球面来保存类内的数据分布，而不是将每个类缩小成一个点。
• 在三个主流的基准数据集（即CARS196 ，CUB-200-2011 和SOP ）上达到了最好水平。

---

Structured Losses

符号：
$X=\{(x_i,y_i){\}}_{i=1}^N$ 是输入数据，$(x_i,y_i)$表示第$i$个图像和它对应的类别标签。类别总数为$C$，例如$y_i\in [1,2,...,C]$;来自第$c$类的图像被表示为$\{N_i^c{\}}_{i=1}^{N_c}$,其中$N_c$是第$c$类图像的数量。

Ranking-Motivated Structured Losses

Triplet Loss

Triplet Loss的目的是用一个固定的间隔使锚点更靠近正点而不是负点。
$$L(X;f)=\frac{1}{|\Gamma |}\sum _{(i,j,k)\in \Gamma }[d_{ij}^2+m-d_{ik}^2{]}_{+}(1)$$
$\Gamma$是三元组集合，$i,j,k$对应地表示锚点、正样本和负样本点的下标，$f$是嵌入函数，$d_{ij}^2=||f(x_i)-f(x_j)|{|}_2$是欧氏距离，$[\cdot {]}_{+}$是hinge函数。

N-pair-mc

不同于Triplet Loss使用单个的正负样本，这个损失函数利用了数据之间的结构信息来学习到更有区别性的表示。具体来说，样本由一个正样本和$N-1$个负样本组成，这$N-1$个负样本来自于$N-1$个不同的类别，即每个类别1个负样本。
$$L(\{(x_i,x_i^{+}){\}}_{i=1}^N;f)=\frac{1}{N}\sum _{i=1}^{N}log\{1+\sum _{j\ne i}\exp (f_i^{\top }{f}_j^{+}-f_i^{\top }{f}_i^{+})\}(2)$$
${\mathrm{f}}_i=f\left({\mathrm{x}}_i\right)$和${\left\{\left({\mathbf{x}}_i,{\mathbf{x}}_i^{+}\right)\right\}}_{i=1}^N$是来自$N$种不同类别的$N$对样本，例如$y_i\ne y_j,\forall i\ne j$。这里$x_i$和$x_{+}$分别表示查询和正样本，$x_j^{+},i\ne j$是负样本。

Lifted Struct

这个目标函数比N-pair-mc更进一步，提出引入所有的负样本，通过促使锚点与一个正样本的距离尽可能近，与所有的负样本的距离都大于$\alpha$。
$$\begin{array}{rl}L(\mathbf{X};f)=& \frac{1}{2|\mathbf{P}|}\sum _{(i,j)\in \mathbf{P}}[\{d_{ij}+\log (\sum _{(i,k)\in \mathbf{N}}\exp \left(\alpha -d_{ik}\right){+\sum _{(j,l)\in \mathbf{N}}\exp \left(\alpha -d_{jl}\right))\}]}_{+}\end{array}(3)$$
$P$和$N$分别表示正对和负对的集合，给一个查询$x_i$，Lifted Struct打算从所有对应的负数据点中识别一个正示例。

Proxy-NCA

这个方法提出的目的是用代理去解决采样的问题。假设$W$代表着训练集中的一小部分数据，在采样时通过选择与$W$中距离最近的一个样本$u$作为代理(proxy), 即：
$$p(\mathbf{u})=\arg \underset{\mathbf{w}\in \mathbf{W}}{\min }d(\mathbf{u},\mathbf{w})(4)$$
$p(u)$表示从$W$到$u$的最近点，基于选择的proxy, 使用传统的NCA损失：
$$L(\mathbf{a},\mathbf{u},\mathbf{Z})=-\log \left(\frac{\exp (-d(\mathbf{a},p(\mathbf{u})))}{{\sum }_{\mathbf{z}\in \mathbf{Z}}\exp (-d(\mathbf{a},p(\mathbf{z})))}\right)(5)$$
$Z$是负样本集， $p(u)$ 、$p(z)$分别表示正样本和负样本的代理,$a$是锚点，$d(\cdot ,\cdot )$是两个点间的欧氏距离。
上述几种损失的示意图如下：

Clustering-Motivated Structured Losses

用到再写吧

上述的损失函数都存在如下的两点局限性：

1. 这些损失函数虽然都提出了加入更多的负样本来获得结构化的信息，但是使用的负样本仅仅是一小部分；
2. 另外这些损失函数没有考虑类内的数据分布，都追求将同一个class压缩到一个点上。

本文基于上述的两个原因，提出了相应的改进措施,也即本文提出的Ranked List Loss（RRL）。

Methodology

目标是学习可判别的的函数$f$（又称深度度量），以使正样本对之间的相似度高于特征空间中负样本对之间的相似度，在这种情况下，给定来自任何类的查询，旨在从所有其他示例中识别其匹配样本。

Pairwise Constraint

为了将正负样本区分开，希望负样本之间的距离大于某个阈值$\alpha$，并且正样本之间的距离小于α-m，即正负样本之间至少有m的间隔。基于此，选择pairwise margin loss作为基本的承兑对比损失去构造基于集合相似度的结构：

给一个图像$x_i$,目标是将其负样本点推到比边界$\alpha$更远的位置，将其正样本点推到比另一个边界$\alpha -m$更近的位置,因此$m$是两个边界的间隔。数学形式：
$$L_{\mathrm{m}}\left({\mathrm{x}}_i,{\mathrm{x}}_j;f\right)=\left(1-y_{ij}\right){\left[\alpha -d_{ij}\right]}_{+}+y_{ij}{\left[d_{ij}-(\alpha -m)\right]}_{+}（8）$$
其中当$y_i=y_j$时，$y_{ij}=1$;反之,$y_{ij}=0$。$d_{ij}={\Vert f({\mathrm{x}}_i)-f({\mathrm{x}}_j)\Vert }_2$是两点间的欧式距离。

Ranked List Loss

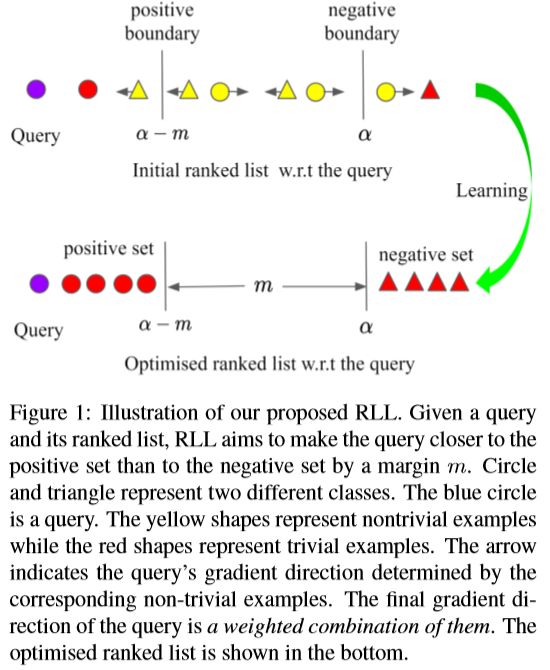
给定一个anchor ($x_i$),基于相似度对其他样本进行排序,如下图所示，在这个排序的结果中，正样本集${\mathbf{P}}_{c,i}=\left\{{\mathbf{x}}_j^c|j\ne i\right\}$,$\left|{\mathbf{P}}_{c,i}\right|=N_c-1$中有$N_c-1$个正样本,同样地，负样本集${\mathbf{N}}_{c,i}=\left\{{\mathbf{x}}_j^k|k\ne c\right\}$,$\left|{\mathbf{N}}_{c,i}\right|={\sum }_{k\ne c}{N}_k$中有${\sum }_{k\ne c}{N}_k$个负样本。

Non-trivial Sample Mining

对样本进行合适采样可以加快模型的收敛速率和提高模型性能，比如常见的难样本挖掘。本文使用的采样策略很简单，就是损失函数不为0的样本(非平凡样本有非零损失，由于它们具有零梯度，因此随着模型的改进，将它们包括在内进行训练将在梯度融合过程中“削弱”非平凡示例的贡献)，具体来说，对于正样本，损失函数不为0意味着它们与anchor之间的距离大于$\alpha -m$, 类似的，对于负样本，损失函数不为0意味着它们与anchor之间的距离小于$\alpha$。
挖掘非平凡正样本和负样本。对于$x_i$,挖掘后的非平凡正样本集表示为$P_{c,i}^{\ast }=\left\{{\mathbf{x}}_j^c|j\ne i,d_{ij}>(\alpha -m)\right\}$；同理，负样本集表示为$N_{c,i}^{\ast }=\left\{{\mathrm{x}}_j^k|k\ne c,d_{ij}<\alpha \right\}$。

Loss-based Negative Examples Weighting
但是存在一个问题就是非平凡负样本的数量通常比较大，并且它们的损失值幅度范围也较大，为了更好的利用它们，作者基于他们损失值进行加权。加权的方式为：
$$w_{ij}=\exp \left(T\cdot \left(\alpha -d_{ij}\right)\right),{\mathrm{x}}_j^k\in {\mathrm{N}}_{c,i}^{\ast }(9)$$
注意到，相对于任何嵌入的梯度幅度在等式（8）中始终为1。数学上：
$${\Vert \frac{\partial L_{\mathrm{m}}\left({\mathrm{x}}_i,{\mathrm{x}}_j;f\right)}{\partial f\left({\mathrm{x}}_j\right)}\Vert }_2={\Vert \frac{f\left({\mathrm{x}}_i\right)-f\left({\mathrm{x}}_j\right)}{{\Vert f\left({\mathrm{x}}_i\right)-f\left({\mathrm{x}}_j\right)\Vert }_2}\Vert }_2=1(10)$$
因此，任何嵌入的梯度大小仅由加权策略$w_{i}j$确定。在这种情况下，评估其影响也很方便。在等式中（9），$T\ge 0$是控制加权负例的程度（斜率）的温度参数。如果$T=0$，它将平等对待所有非平凡的否定例子。如果$T=+\infty$，它将成为最难的负示例挖掘。

Optimisation Objective
对于每个anchor, 希望使得它与正样本集$P$的距离越近越好，并且与负样本集$N_{c,i}$之间存在着$m$的间隔，同时，我们还希望使得负样本的之间大于边界$\alpha$。因此相当于使得同一类别位于一个半径为$\alpha -m$大小的超球体内。
为了将$P_{c,i}^{\ast }$中所有非平凡的正样本点汇集在一起并学习一个类超球面，最小化下列损失：
$$L_{\mathrm{P}}\left({\mathrm{x}}_i^c;f\right)=\frac{1}{\left|{\mathbf{P}}_{c,i}^{\ast }\right|}\sum _{{\mathbf{x}}_j^c\in {\mathbf{P}}_{c,i}^{\ast }}{L}_{\mathrm{m}}\left({\mathrm{x}}_i^c,{\mathrm{x}}_j^c;f\right)(11)$$
不加劝正样本是因为仅仅存在很少正样本。同理，为了拉远$N_{c,i}^{\ast }$中的非平凡负样本超过边界$\alpha$，需要最小化下列式子：
$$L_{\mathrm{N}}\left({\mathrm{x}}_i^c;f\right)=\sum _{{\mathbf{x}}_j^k\in \left[{\mathbf{N}}_{c,i}^{\ast }\right]}\frac{w_{ij}}{{\sum }_{{\mathbf{x}}_j^k\in \left[{\mathbf{N}}_{c,1}^{\ast }\right]}{w}_{ij}}{L}_{\mathrm{m}}\left({\mathrm{x}}_i^c,{\mathrm{x}}_j^k;f\right)(12)$$
因此，整个损失函数为：
$$L_{\mathrm{R}\mathrm{L}\mathrm{L}}\left({\mathrm{x}}_i^c;f\right)=L_{\mathrm{P}}\left({\mathrm{x}}_i^c;f\right)+\lambda L_{\mathrm{N}}\left({\mathrm{x}}_i^c;f\right)(13)$$
$\lambda$控制正负样本集间的平衡，实验中设为1。将其他样本的特征视为常量。 因此，只有$f(x_i^c)$是根据其他元素加权组合的影响进行更新的。

算法流程如下：

---

论文链接 : https://arxiv.org/pdf/1903.03238.pdf