2020蓝桥杯JAVA A组填空题
参加了本届蓝桥杯JAVA A组,有幸进入国赛,于是回顾下省赛的填空题,大题到时再回忆下,下面思路仅供参考。
A 门牌制作
【问题】小蓝要为一条街的住户制作门牌号。这条街一共有2020 位住户,门牌号从1 到2020 编号。小蓝制作门牌的方法是先制作0 到9 这几个数字字符,最后根据需要将字符粘贴到门牌上,例如门牌1017 需要依次粘贴字符1、0、1、7,即需要1 个字符0,2 个字符1,1 个字符7。请问要制作所有的1 到2020 号门牌,总共需要多少个字符2?
【思路】遍历1到2020,数2的个数就好。
public static void main(String[] args) {
int ans=0;
for (int i = 1; i <= 2020; i++) {
char[] c=Integer.toString(i).toCharArray();
for (int j = 0; j < c.length; j++) {
if (c[j]=='2') {
ans++;
}
}
}
System.out.println(ans);
}
运行结果
624
B 既约分数
【问题】如果一个分数的分子和分母的最大公约数是1,这个分数称为既约分数。例如,3/4 , 5/2 , 1/8 , 7/1都是既约分数。请问,有多少个既约分数,分子和分母都是1 到2020 之间的整数(包括1和2020)?
【思路】暴力枚举,每次判断分子和分母是否互质就OK了
public class Two {
//求两数的最大公约数
static int gcd(int a,int b){
int t;
if(a<b){
t=a;
a=b;
b=t;
}
while(a%b!=0){
t=b;
b=a%b;
a=t;
}
return b;
}
public static void main(String[] args) {
int ans=0;
for (int i = 1; i <= 2020; i++) {
for (int j = 1; j <= 2020; j++) {
if (gcd(i, j)==1)ans++;
}
}
System.out.println(ans);
}
}
运行结果
2481215
C 蛇形填数
【问题】如下图所示,小明用从1 开始的正整数“蛇形”填充无限大的矩阵。
| 1 | 2 | 6 | 7 | 15 | … |
|---|---|---|---|---|---|
| 3 | 5 | 8 | 14 | … | |
| 4 | 9 | 13 | … | ||
| 10 | 12 | … | |||
| 11 | … | ||||
| … |
容易看出矩阵第二行第二列中的数是5。请你计算矩阵中第20 行第20 列的数是多少?
【思路】一个思路是可以老老实实按着要求斜着走,下面提供了这种思路代码;另一种可以观察题目问的是20行20列,即对角线中间位置,可以发现,对角线中间位置无论怎么绕,都是不变的,因此可以顺序输出金字塔形,如下图:
| 1 | ||||||
|---|---|---|---|---|---|---|
| 2 | 3 | |||||
| 4 | 5 | 6 | ||||
| 7 | 8 | 9 | 10 | |||
| … | … |
第20行20列对应金字塔的39行中间的数。
public class Three {
public static void main(String[] args) {
boolean flag = true;
for (int x = 1, y = 1, k = 1; ; k++) {
if (x == 20 && y == 20) {
System.out.println(k);
break;
}
if (flag){//斜向下走
if (x - 1!=0){
x--;
y++;
}
else {//到左边界时,直接下走
y++;
flag = false;
}
}
else {//斜向上走
if (y - 1!=0) {
x++;
y--;
}
else {
x++; //到上边界时,直接横走
flag = true;
}
}
}
}
}
运行结果
761
D 七段码
【问题】小蓝要用七段码数码管来表示一种特殊的文字。
七段码上图给出了七段码数码管的一个图示,数码管中一共有7 段可以发光的二极管,分别标记为a, b, c, d, e, f, g。小蓝要选择一部分二极管(至少要有一个)发光来表达字符。在设计字符的表达时,要求所有发光的二极管是连成一片的。
例如:b 发光,其他二极管不发光可以用来表达一种字符。
例如:c 发光,其他二极管不发光可以用来表达一种字符。这种方案与上一行的方案可以用来表示不同的字符,尽管看上去比较相似。
例如:a, b, c, d, e 发光,f, g 不发光可以用来表达一种字符。
例如:b, f 发光,其他二极管不发光则不能用来表达一种字符,因为发光的二极管没有连成一片。
请问,小蓝可以用七段码数码管表达多少种不同的字符?
【思路】利用dfs选择排列,枚举所有情况,再利用邻接表判断每种情况是否连成一片,是的话就计数,结果输出了所有可行情况。
public class Four {
static String s="abcdefg";
static char[] c=s.toCharArray();
static int vis[]=new int[7];
static char[][]table={//建立邻接表
{'b','f'},{'a','g','c'},{'b','g','d'},
{'c','e'},{'f','g','d'},{'a','g','e'},
{'f','b','c','e'}
};
static int ans=0;
static boolean check(String s){//判断选择的二极管能否连成一片
char[] num=s.toCharArray();
for (int i = 0; i < num.length; i++) {
boolean flag0=false;
for (int j = 0; j < num.length; j++) {
boolean flag=false;
for (int k = 0; k < table[num[i]-'a'].length; k++) {
if (num[j]==table[num[i]-'a'][k]) {
flag=true;
break;
}
}
if (flag) {
flag0=true;
break;
}
}
if (flag0==false) {
return false;
}
}
return true;
}
static void dfs(int step,int pos,int n,int k,String s){
if (step==k) {
if (k==1) {
System.out.println(s);
ans++;
}
else {
if (check(s)) {
System.out.println(s);
ans++;
}
}
return;
}
if (pos==n) {
return;
}
if (vis[pos]==0) {
vis[pos]=1;
dfs(step+1, pos, n, k, s+c[pos]);
vis[pos]=0;
}
dfs(step, pos+1, n, k, s);
}
public static void main(String[] args) {
for (int i = 1; i <= 7; i++) {
dfs(0, 0, 7, i, "");
}
System.out.println(ans);
}
}
运行结果
a
b
c
d
e
f
g
ab
af
bc
bg
cd
cg
de
ef
eg
fg
abc
abf
abg
aef
afg
bcd
bcg
beg
bfg
cde
cdg
ceg
cfg
def
deg
efg
abcd
abcf
abcg
abde
abef
abeg
abfg
acdf
acfg
adef
aefg
bcde
bcdg
bcef
bceg
bcfg
bdeg
befg
cdef
cdeg
cdfg
cefg
defg
abcde
abcdf
abcdg
abcef
abceg
abcfg
abdef
abdeg
abefg
acdef
acdfg
acefg
adefg
bcdef
bcdeg
bcdfg
bcefg
bdefg
cdefg
abcdef
abcdeg
abcdfg
abcefg
abdefg
acdefg
bcdefg
abcdefg
83
E 平面分割
【问题】20个圆和20 条直线最多能把平面分成多少个部分?
【思路】下面是我自己画图找规律的分析,似乎是这样子,不确保答案对不对,如有问题,欢迎指正。
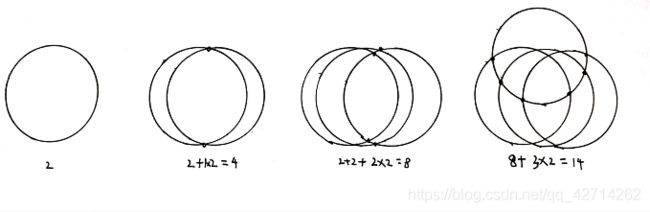
1.先考虑只有圆的情况
- 一个圆最多能把平面分成2个部分,
- 2个圆最多能把平面分成4个部分;
- 3个圆最多能把平面分成8个部分;
- 现在加入第4个圆,为了使分成的部分最多,第4个圆必须与前面3个圆都有两个交点,因此得6个交点将第4个圆的圆周分成6段圆弧,而每一段圆弧将原来的部分一分为二,即平面增加了一个部分,于是4个圆最多将平面分成8+6=14个部分,
- 同理,5个圆最多将平面分成14+8=22个部分
- 最终可推算出n个圆最多把平面分成2+1x2+2x2+…+(n-1)x2部分
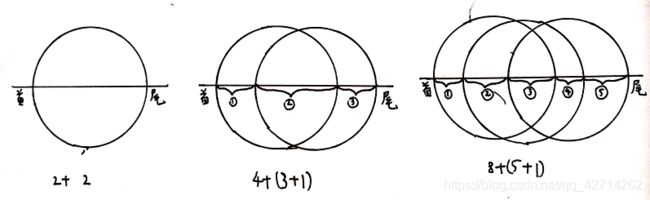
2.再考虑引入1条直线的情况
- 假设只有一个圆,其把平面分成2部分
- 引入一条直线,一条直线最多和此圆有2个交点,此直线被分成3段,中间一段把原来部分一分为2,首尾共同把原来部分一分为2,因此平面增加1+1=2部分,得2+2=4
- 如果有两个圆,两个圆最多把平面分成4部分,那么一条直线最多和两个圆有4个交点,直线被分成5段有中间三段把原来部分一分为二,首尾共同把原来部分一分为2,因此平面增加3+1=4
- 如果有三个圆,三个圆最多把平面分成8部分,那么一条直线最多和三个圆有6个交点,直线被分成7段,中间5段段把原来部分一分为二,首尾共同把原来部分一分为2,因此平面增加5+1=6
- 可总结出,引入一条直线,原来的n个圆会把直线最多分成2n+1段,平面增加2n部分
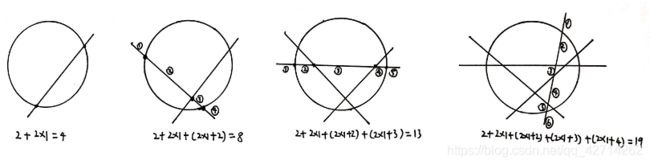
3.最后考虑引入m条直线的情况
首先每条直线都会最多与原来的圆有2n个交点,平面增加2n部分。再此基础上,我们再考虑直线与直线相交的情况,为方便画图找规律,设n=1。
- 引入1条直线,其和圆最多2个交点,此直线被分成3段,中间一段把原来部分一分为2,首尾共同把所在区域一分为2,因此平面增加2x1=2部分
- 引入第2条直线,其和圆与之前直线最多产生2x1+1=3个交点,此直线被分成2x1+2=4段,每段把其所在区域一分为二,因此平面增加4部分
- 引入第3条直线,其和圆与之前直线最多产生2x1+2=4个交点,此直线被分成2x1+3=5段,每段把其所在区域一分为二,因此平面增加5部分;
- 引入第4条直线,其和圆与之前直线最多产生2x1+3=5个交点,此直线被分成2x1+4=6段,每段把其所在区域一分为二,因此平面增加6部分;
由此总结一般规律,引入第m条直线,其和n个圆与之前m-1直线最多产生2n+m-1个交点,此直线被分成2n+m段,每段把其所在区域一分为二,因此平面增加2n+m部分(m>=2,当m=1时,增加2n部分);
public class Five {
public static void main(String[] args) {
int ans=2;//第一个圆把平面分成2部分
for (int i = 1; i <= 20; i++) {
ans+=(i-1)*2;//第i个圆依次和前面(i-1)个圆产生(i-1)*2个交点,即被分成(i-1)*2段,亦即产生(i-1)*2个部分
}
System.out.println(ans);
int n=20;
ans+=n*2;//第一条直线和20个圆相交,平面增加2*n部分
for (int i = 2; i <=20 ; i++) {
ans+=(2*n+i);//第i条直线和前面20个圆和i-1条线最多产生40+i-1个焦点,被分成40+i段,亦即增加40+i个部分
}
System.out.println(ans);
}
}
运行结果
1391