python实现梯度下降法
文章目录
- 一、什么是梯度下降法
- 二、如何理解梯度下降法
-
-
- 2.1 概念
- 2.2 举例说明
-
- 三、求解梯度下降法
- 四、python编程演算】
- 五、资料引用
一、什么是梯度下降法
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。
二、如何理解梯度下降法
2.1 概念
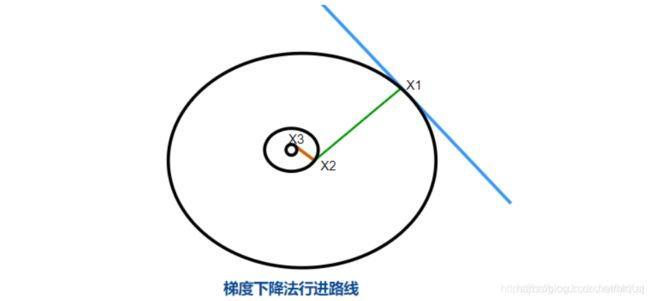
顾名思义,梯度下降法的计算过程就是沿梯度下降的方向求解极小值(也可以沿梯度上升方向求解极大值)。
其迭代公式为 ,其中代表梯度负方向,表示梯度方向上的搜索步长。梯度方向我们可以通过对函数求导得到,步长的确定比较麻烦,太大了的话可能会发散,太小收敛速度又太慢。一般确定步长的方法是由线性搜索算法来确定,即把下一个点的坐标看做是ak+1的函数,然后求满足f(ak+1)的最小值的ak+1即可。
因为一般情况下,梯度向量为0的话说明是到了一个极值点,此时梯度的幅值也为0.而采用梯度下降算法进行最优化求解时,算法迭代的终止条件是梯度向量的幅值接近0即可,可以设置个非常小的常数阈值。
2.1.1 微分理解
我们所要优化的函数必须是一个连续可微的函数,可微,既可微分,意思是在函数的任意定义域上导数存在。如果导数存在且是连续函数,则原函数是连续可微的。
梯度下降法的基本思想:梯度下降法(Gradient Descent) –
现代机器学习的血液
- 函数图像中,某点的切线的斜率
- 函数的变化率
以二元函数z=f(x,y)为例,假设其对每个变量都具有连续的一阶偏导数例 ∂ u ∂ x \frac{\partial u}{\partial x} ∂x∂u和 ∂ u ∂ y \frac{\partial u}{\partial y} ∂y∂u,则这两个偏导数构成的向量[ ∂ u ∂ x \frac{\partial u}{\partial x} ∂x∂u, ∂ u ∂ y \frac{\partial u}{\partial y} ∂y∂u],即为该二元函数的梯度向量,一般记作∇ f(x,y),其中∇读作“Nabla”。
例子:
J(Θ) = 0.55 -(5θ1+2θ2-12θ3)
∇J(Θ) = [ ∂ J ∂ θ 1 \frac{\partial J}{\partial θ _1 } ∂θ1∂J, ∂ J ∂ θ 2 \frac{\partial J}{\partial θ _2} ∂θ2∂J, ∂ J ∂ 3 \frac{\partial J}{\partial _3 } ∂3∂J] = [−5,−2,12]
梯度的意义:
- 在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
- 在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
从几何意义来讲,梯度的方向表示的是函数增加最快的方向,这正是我们下山要找的“最陡峭的方向”的反方向!因此后面要讲到的迭代公式中,梯度前面的符号为“-”,代表梯度方向的反方向。
2.2 举例说明
举一个非常简单的例子,如求函数f(x) = x² 的最小值。
利用梯度下降的方法解题步骤如下:
- 1、求梯度,∇ = 2x
- 2、向梯度相反的方向移动x ,如下

- 3、循环迭代步骤2,直到x 的值变化到使得 f(x)在两次迭代之间的差值足够小,比如0.00000001,也就是说,直到两次迭代计算出来的 f(x)基本没有变化,则说明此时 f(x)已经达到局部最小值了。
- 4、此时,输出x ,这个 x就是使得函数f(x) 最小时的 x的取值 。

三、求解梯度下降法
问题描述:
f ( X ) = f ( x 1 , x 2 ) = 1 3 x 1 2 + 1 2 x 2 2 f(X)\,=f(x_1,x_2)=\frac{1}{3}x_1^2+\frac{1}{2}x_2^2 f(X)=f(x1,x2)=31x12+21x22的 极小值点。
解:设初始点为 X 1 = ( 3 , 2 ) X _1 = ( 3 , 2 ) X1=(3,2),学习率为 α \alpha α 。
∇ f ( X 1 ) = ( 2 3 ) × 3 , 2 2 × 2 ) = ( 2 , 2 ) \nabla f(X_1)=(\frac{2}{3})\times3,\frac{2}{2}\times2)=(2,2) ∇f(X1)=(32)×3,22×2)=(2,2)
因此更新迭代公式带入原函数中,得:
f ( X 2 ) = f ( X 1 − α ∇ f ( X 1 ) ) = 10 3 α 2 − 8 α + 5 f(X_2)=f(X_1-\alpha\nabla f(X_1))=\frac{10}{3}\alpha^2-8\alpha+5 f(X2)=f(X1−α∇f(X1))=310α2−8α+5
此时, α 1 ∗ = 6 5 \alpha_1^*=\frac{6}{5} α1∗=56时,为函数极小点。
因此,再将 X 2 X_2 X2 作为初始点,重复上面的迭代步骤,
得到: X 3 = ( 3 5 2 , 2 5 2 ) X_3=(\frac{3}{5^2},\frac{2}{5^2}) X3=(523,522)
根据规律显然可知: X k = ( 3 5 k − 1 , ( − 1 ) k − 1 , 2 5 k − 1 ) X_k=(\frac{3}{5^k-^1},(-1)^k-^1,\frac{2}{5^k-^1}) Xk=(5k−13,(−1)k−1,5k−12)
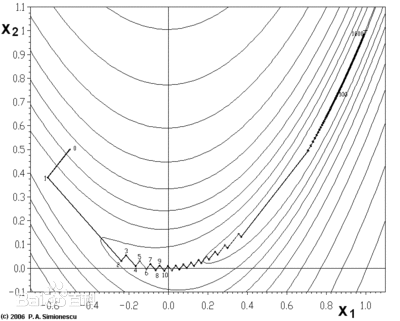
例中目标函数 f ( X ) f(X) f(X)是三维空间中的椭圆抛物面,其投影至二维空间上的等高线是一簇椭圆(下图所示)。 f ( X ) f(X) f(X)的极小点就是这簇椭圆的中心 X ∗ = ( 0 , 0 ) X*=(0,0) X∗=(0,0)。我们求得的迭代公式{ X k X_k Xk}是逐渐趋近于 X ∗ X^* X∗的。
四、python编程演算】
实验环境:
python3.8
函数:
z = 2 ( x − 1 ) 2 + y 2 z=2(x-1)^2+y^2 z=2(x−1)2+y2
求出:
( ∂ z ∂ x , ∂ z ∂ y ) = ( 4 x − 4 , 2 y ) (\frac{\partial z}{\partial x },\frac{\partial z}{\partial y})=(4x-4,2y) (∂x∂z,∂y∂z)=(4x−4,2y)
4.1 初始设定
给出初始位置 ( x i , y i ) , i = 0 (x_i,y_i),i=0 (xi,yi),i=0与学习率 α = 0.1 \alpha=0.1 α=0.1
源码:
# 导入所需库
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings
# 原函数
def Z(x,y):
return 2*(x-1)**2 + y**2
# x方向上的梯度
def dx(x):
return 4*x-4
# y方向上的梯度
def dy(y):
return 2*y
# 初始值
X = x_0 = 3
Y = y_0 = 2
# 学习率
alpha = 0.1
# 保存梯度下降所经过的点
globalX = [x_0]
globalY = [y_0]
globalZ = [Z(x_0,y_0)]
# 迭代30次
for i in range(30):
temX = X - alpha * dx(X)
temY = Y - alpha * dy(Y)
temZ = Z(temX, temY)
# X,Y 重新赋值
X = temX
Y = temY
# 将新值存储起来
globalX.append(temX)
globalY.append(temY)
globalZ.append(temZ)
# 打印结果
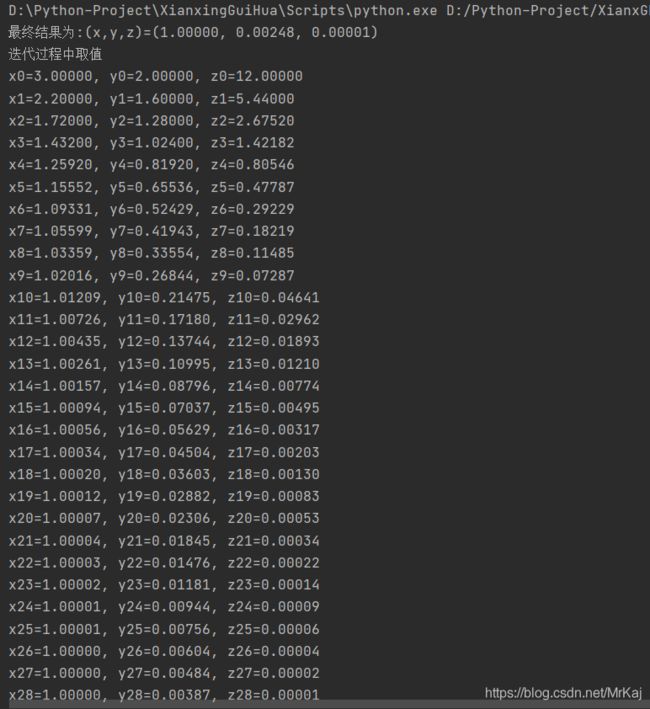
print(u"最终结果为:(x,y,z)=(%.5f, %.5f, %.5f)" % (X, Y, Z(X,Y)))
print(u"迭代过程中取值")
num = len(globalX)
for i in range(num):
print(u"x%d=%.5f, y%d=%.5f, z%d=%.5f" % (i,globalX[i],i,globalY[i],i,globalZ[i]))
五、资料引用
Excel和Python实现梯度下降法