机器学习：随机梯度下降法

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDClassifier
from sklearn.datasets.samples_generator import make_blobs

##生产数据
X, Y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60)

##训练数据
clf = SGDClassifier(loss="hinge", alpha=0.01)
clf.fit(X, Y)

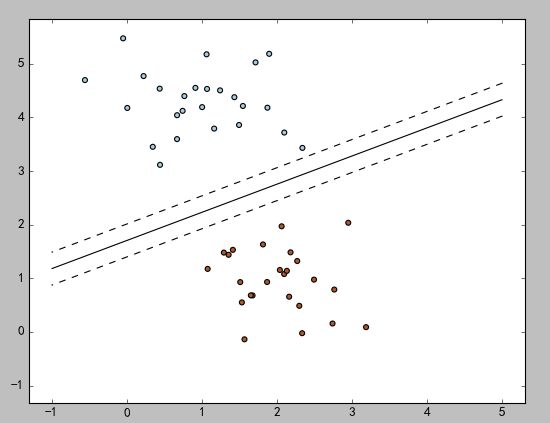
## 绘图
xx = np.linspace(-1, 5, 10)
yy = np.linspace(-1, 5, 10)

##生成二维矩阵
X1, X2 = np.meshgrid(xx, yy)
##生产一个与X1相同形状的矩阵
Z = np.empty(X1.shape)
##np.ndenumerate 返回矩阵中每个数的值及其索引
for (i, j), val in np.ndenumerate(X1):
    x1 = val
    x2 = X2[i, j]
    p = clf.decision_function([[x1, x2]]) ##样本到超平面的距离
    Z[i, j] = p[0]
levels = [-1.0, 0.0, 1.0]
linestyles = ['dashed', 'solid', 'dashed']
colors = 'k'
##绘制等高线：Z分别等于levels
plt.contour(X1, X2, Z, levels, colors=colors, linestyles=linestyles)
##画数据点
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired,
            edgecolor='black', s=20)
plt.axis('tight')
plt.show()

梯度下降的变形形式

         根据处理的训练数据的不同，主要有以下三种形式：

       1）批量梯度下降法BGD(Batch Gradient Descent):

             针对的是整个数据集，通过对所有的样本的计算来求解梯度的方向。

             优点：全局最优解；易于并行实现；

             缺点：当样本数据很多时，计算量开销大，计算速度慢

        2）小批量梯度下降法MBGD（mini-batch Gradient Descent）

            把数据分为若干个批，按批来更新参数，这样，一个批中的一组数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性

            优点：减少了计算的开销量，降低了随机性

         3）随机梯度下降法SGD（stochastic gradient descent）

            每个数据都计算算一下损失函数，然后求梯度更新参数。

            优点：计算速度快

            缺点：收敛性能不好

        总结：SGD可以看作是MBGD的一个特例，及batch_size=1的情况。在深度学习及机器学习中，基本上都是使用的MBGD算法。

随机梯度下降（SGD）是一种简单但非常有效的方法，多用用于支持向量机、逻辑回归等凸损失函数下的线性分类器的学习。并且SGD已成功应用于文本分类和自然语言处理中经常遇到的大规模和稀疏机器学习问题。

       SGD既可以用于分类计算，也可以用于回归计算。

    1）分类

        a）核心函数

            sklearn.linear_model.SGDClassifier

       b）主要参数（详细参数）

            loss ：指定损失函数。可选值：‘hinge’(默认), ‘log’, ‘modified_huber’, ‘squared_hinge’, ‘perceptron’,

                       "hinge":线性SVM
                       "log":逻辑回归
                       "modified_huber":平滑损失，基于异常值容忍和概率估计
                       "squared_hinge": 带有二次惩罚的线性SVM
                       "perceptron":带有线性损失的感知器

             alpha:惩罚系数

回归

         SGDRegressor非常适合回归问题具有大量训练样本（> 10000），对于其他的问题，建议使用的Ridge， Lasso或ElasticNet。

        a）核心函数

             sklearn.linear_model.SGDRegressor

        b）主要参数（详细参数）

             loss：指定损失函数。可选值‘squared_loss’（默认）, ‘huber’, ‘epsilon_insensitive’,  ‘squared_epsilon_insensitive’

                     说明：此参数的翻译不是特别准确，请参考官方文档。

                    "squared_loss":采用普通最小二乘法
                    "huber": 使用改进的普通最小二乘法，修正异常值
                    "epsilon_insensitive": 忽略小于epsilon的错误
                    "squared_epsilon_insensitive":

             alpha:惩罚系数

         c）示例代码

              因为使用方式与其他线性回归方式类似，所以这里只举个简单的例子： 

import numpy as np
from sklearn import linear_model
n_samples, n_features = 10, 5
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
clf = linear_model.SGDRegressor()
clf.fit(X, y)