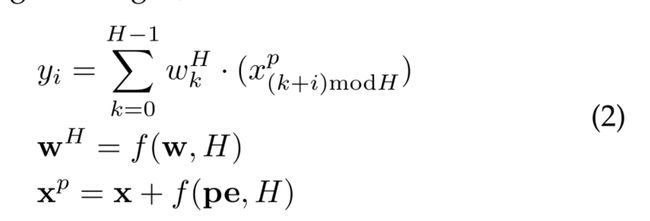Fast-ParC学习笔记

Fast-ParC学习笔记

Fast-ParC: Position Aware Global Kernel for ConvNets and ViTs

Abstract

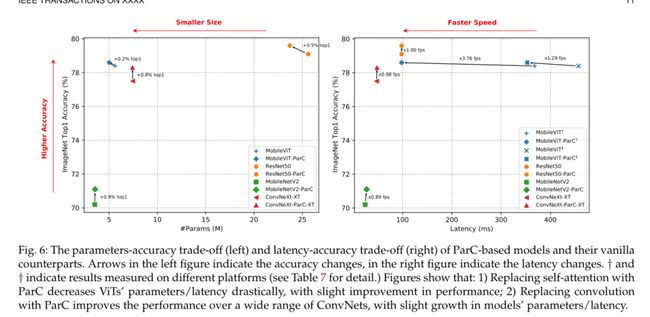
近年来，T型变压器模型在各个领域都取得了长足的进步。在计算机视觉领域，视觉变压器(ViTs)也成为卷积神经网络(ConvNets)的有力替代品，但由于卷积神经网络和视觉变压器都有各自的优点，所以它们无法取代卷积神经网络。例如，vit善于利用注意机制提取全局特征，而ConvNets则因其强烈的归纳偏差而更有效地建模局部关系。一个自然产生的想法是结合ConvNets和vit的优点来设计新的结构。本文提出了一种新的基本神经网络算子——位置感知圆卷积(ParC)及其加速版Fast-ParC。ParC算子可以通过使用全局核和循环卷积捕获全局特征，同时通过使用位置嵌入保持位置敏感性。我们的Fast-ParC使用快速傅里叶T变换进一步将ParC的$O(n^2)$时间复杂度降低到$O(nlogn)$。这种加速使得在具有大型特征映射的模型的早期阶段使用全局卷积成为可能，但仍然保持与使用3x3或7x7核相比的总体计算成本.该操作可以plug-and-play(即插即用)地实现1)将vit转换为纯convnet架构，以获得更广泛的硬件支持和更高的推理速度;2)在卷积网络的深层阶段取代传统的卷积，通过扩大有效接受域来提高精度。实验结果表明，我们的ParC op可以有效地扩大传统ConvNets的接受域，采用所提出的op对ViTs和ConvNet模型在图像分类、目标检测和语义分割这三种常见视觉任务上都有优势。

https://github.com/yangtao2019yt/Fast_ParC.git.

Index Terms: 全局感受域，位置感知圆卷积，位置嵌入，纯卷积运算，快速傅里叶变换

1 INTRODUCTION

近年来，vision变压器已逐渐兴起。Transformer在2017年首次提出，用于解决NLP任务[2]。2020年，Dosovitskiy等人[3]直接将原始变压器应用于图像分类任务，发现在大型数据集(例如ImageNet-21K或JFM-300M[4])上预训练时，它取得了比卷积网络(ConvNets)更好的结果。ViT及其变体随后被广泛应用于其他下游视觉任务，如物体检测[5][6]、语义分割[7]和多模态任务，如人-物交互(HOI)[8]、文本-图像合成(T2I)[9]等。尽管变压器取得了巨大的成功，但它们仍然不能完全取代ConvNets。如前文[1][10][11][12]总结，与ViTS相比，ConvNets有更好的硬件支持，更容易训练。此外，ConvNets在移动和其他边缘计算场景的轻量级模型[13][14]领域仍然占主导地位。

变压器和convnet都有各自的特点。对于变压器，广泛公认的多头注意机制被设计来捕获令牌之间的远程成对关系，这提供了具有强大全局建模能力的transformer。在获得这种表示能力的同时，也需要较高的计算预算。自我注意的时间复杂度是令牌数量的二次方，因此处理高分辨率特征映射的速度较慢。与之不同的是，卷积运算擅长于提取局部信息。它在一个小的滑动窗口(通常为3x3)内捕获局部信息，并对不同的输入和不同的空间位置重用相同的卷积核。它可以被解释为一种有效的隐式权值共享方案，使卷积所需参数仅随输入线性增长。此外，ConvNets已经得到了很长时间的研究和使用，因此它们还具有其他一些独特的优势。例如，对于ConvNets，像修剪[17]和量化[18]这样的压缩算法是成熟的。至于硬件实现，也有许多现有的加速方案(例如Winograd [19]， FFT [20]， im2col[21])，无论是在一般的平台上，如CPU, GPU或专用的加速器，如FPGA, ASIC。总之，卷积运算实现成本较低，但不能像自我注意那样捕捉全局关系。显然，在变压器的表示能力和卷积网络的效率之间存在着一种互补关系，两者对于实际应用都是不可或缺的。

最近有一些结合变压器和convnet优点的工作。PVT [22]， Swin[23]和CoAtNet[24]试图重新引入卷积的归纳偏差(例如它的滑动窗口策略)，以帮助变压器模型更好地学习。就像LeViT [25]，MobileViT [11]， EfficientFormer[26]专注于设计高效的混合架构。这些工作大多将这两种网络结合在一起，但它们未能解决关键问题:新引入的注意算子的额外计算和工程复杂性。人们很自然地会问:是否有可能设计出一种不同于自注意和传统卷积的新算子，同时具有两者的优点?

本文结合变压器和ConvNets的优点，构造了一个新的即插即用算子ParC。由于采用全局核($K_h=H或K_w=W$)，并采用循环卷积方案，ParC具有全局接受域。然后在卷积前采用显式可学习的位置嵌入，以保持模型的位置敏感性。如图1所示，不同的ConvNet模型通过简单地应用所提出的ParC算子将其有效接受域提高为全局的。由于ParC采用纯卷积运算，在不同平台上部署效率高。最后，我们将二维卷积分解为两个一维卷积，以克服flop /参数的增加。基于上述设计，我们实现了提取全局特征的目标，同时在空间和时间复杂度上保持了较低的成本。通过实验，我们验证了新算子在广泛的任务和模型中的有效性。总之，本文的贡献可以概括为以下三点:

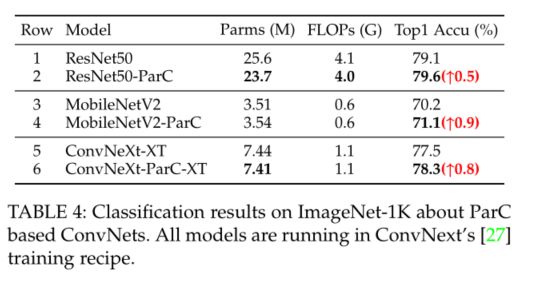
1)结合ViTs和ConvNets的优点，提出了一种有效的新算子ParC。实验证明了ParC的优势，将其应用于广泛的模型，包括MobileViT [27]， ResNet50 [28]， MobileNetV2[14]和ConvNext[27]。我们还在多个任务上评估这些模型，包括分类、检测和分割。

2)针对输入特征分辨率较大时ParC算法复杂度过大的问题，提出了快速ParC算法。Fast-Parc在理论上等同于ParC，例如，当给定相同的输入时，它们的输出是相同的。然而，当给出大分辨率时，它比ParC要高效得多(例如112×122)。Fast-ParC扩展了ParC的使用场景，使其成为一个应用范围更广的运营商。

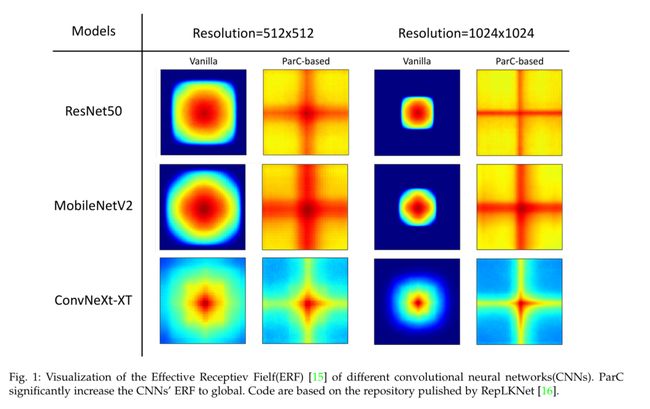
3)分析了新算子的内在机理。通过可视化，我们展示了ParC和纯卷积之间的几个明显区别。研究表明，普通ConvNet的有效接受域[15]是非常有限的，而基于parcel的网络的有效接受域[15]是全局的。我们还通过Grad-CAM[29]表明，基于parcel的网络在聚焦图像的重要区域方面比普通的ConvNets更全面。我们还详细分析了ParC和香草卷积的区别。

2 RELATER WORK

2.1 Theoretical/Effective Receptive Field

Hebel等[30]在神经科学中发现，浅层神经元只提取局部特征，覆盖的范围层层累积，称为“接受野(RF)”。自从VGGNet[31]成功以来，CNN架构的设计遵循类似的模式[28] [32] [14] [13]-使用小内核的堆叠，如3×3，而不是较大的内核。前人的一些工作给出了CNN的感受野[33] [34]的理论计算，即理论感受野(TRF)，在此概念下，3×3的两层感受野等于5×5的一层感受野。然而，一些作品[15] [34]对这一观点提出了质疑，因为事实上像素的重要性在特征图中从中心迅速退化到边缘。随后，提出了有效感受野(ERF)来测量输入图像中实际影响神经元激活模式的区域。Luo等人[15]反向传播中心像素，并计算输入图像的偏导数来检查该区域。通过研究一系列的卷积网络，他们发现有效的接受电场通常比理论的要小得多。SKNet[35]采用注意机制选择合适的感受野。RF-Next[36]提出了一个基于nas的工作流来自动搜索模型的接收域。这些工作表明，适当的接受域的确定对网络的性能是非常有益的。最近的研究还发现，增大卷积网络的接受域可以获得更好的模型性能。我们称之为“大核卷积网络”，这将在后面的2.3节中讨论。

2.2 Vision Transformer and Hybrid Structures

ViTs在各种视觉任务中取得了令人印象深刻的表现。但是，最初的ViT[3]有一些限制。例如，它的权重大，计算效率低，难以训练。为了克服这些问题，提出了vit的后续变体。从改进训练策略的角度出发，Touvron等[37]提出使用知识蒸馏来训练ViT模型，并以较少的训练前数据达到竞争精度。为了进一步改进模型体系结构，一些研究人员尝试借鉴ConvNets对ViTs进行优化。其中，PVT[22]和CVT[38]在ViT的每个阶段插入卷积运算，减少令牌数量，构建层级化的多级结构。Swin变压器[23]在移位的局部窗口内计算自注意。PiT[39]联合使用池化层和深度卷积层实现信道倍增和空间约简。CCNet[40]提出了一种简化版的自我注意机制——交叉注意，并将其插入到ConvNets中，构建具有全局接受场的ConvNets。这些论文清楚地表明，ConvNets的一些技术可以应用于视觉变压器，以设计更好的视觉变压器模型。

另一个流行的研究方向是结合vit和ConvNets的元素来设计新的骨干。Graham等人在他们的LeViT[25]模型中混合了ConvNet和变压器，该模型在速度/精度权衡方面显著优于以前的ConvNet和ViT模型。BoTNet[41]在ResNet的最后几个块用多头注意代替了标准的卷积。vit-c[42]为纯ViT添加早期卷积。ConViT[43]通过门控位置自注意融合了软卷积归纳偏差。CMT[10]块由基于深度卷积的局部感知单元和一个轻型变压器模块组成。CoatNet[24]融合了卷积和自关注，设计了一个新的变压器模块，它既关注局部信息，也关注全局信息。

2.3 Large Kernel Convolution Network

早期的ConvNets如AlexNet[44]和GoogleNet[45]使用大内核，如5×5或7×7。但是自从VGGNet[31]成功之后，堆积像3x3和1x1这样的小内核被认为是计算和存储的有效选择。最近，受视觉变形器成功的启发，大内核再次被重用为改进模型性能的强大工具。ConvNext[27]通过引入一系列增量但有效的设计，使标准ResNet朝着视觉转换器的设计现代化，其中7×7深度卷积遵循Swin[23]中的窗口- sa的精神使用。RepLKNet[16]将卷积核扩展到31×31并获得性能增益，但是使用的重新参数化技巧会增加训练过程的负担，并且需要一个额外的转换步骤来部署模型。后来，Rao等人使用了一个更大的内核51×51，它具有动态稀疏度[46]。GFNet[47]用一个全局傅里叶卷积代替变压器块中的SA(自我注意)，用FFT实现。

我们的工作与RepLKNet[16]和GFNet[47]密切相关。这些方法和我们提出的ParC方法都关注于扩大有效接受域，但我们提出的op不同于以下观点:1)我们的ParC使用可学习的位置嵌入来保持结果特征图的位置敏感。这对于位置敏感的任务(如语义分割和目标检测)非常重要。烧蚀研究的实验也证实了这一点。2)我们的ParC采用轻量化设计。RepLKNet使用重二维卷积核，GFNet使用形状为2CHW的可学习复权矩阵，而我们使用两个一维卷积，将核减少为CH或CW。3)不同于强调网络整体设计的RepLKNet和GFNet，我们提出的ParC是一种新型的基础算子，可以插入到vit和ConvNets中，即插即用。我们在4.1节和4.2节的实验结果验证了这一点。此外，我们还提出了Fast-ParC，进一步拓宽了ParC的使用场景。

3 THE PROPOSED FAST-PARC OPERATOR

在本节中，我们首先通过与普通卷积算子的比较来介绍所提出的ParC算子。然后，我们提出了FFT加速版本的ParC，命名为Fast-ParC。最后，我们解释了如何在ViT和ConvNet模型中使用所提出的ParC。

3.1 ParC Operation

3.1.1 Vanilla Depth-wise Convolution

为了描述在形状为B×C×H×W的4D输入张量上进行的水平维一维深度卷积(记为Conv1d-H)，我们可以首先关注一个特定的通道。我们将输出表示为$y=y_1，\dots ，y_{H-1}$，输入为$x=x_0,x_1，\dots ，x_{H-1}$，卷积权值为$w=w_0,w_1，\dots ,w_{K_h-1}$}。带零填充的pytorch式卷积(即f.c conv1d)可以表示为

其中$K_h/2$用于抵消输入两端$K_h/2$标量的额外填充。公式1表明yi是它的局部邻近输入的函数(即$x_i-K_h/2，\dots ，x_{K_h/2-1+i}$)，邻域的大小由核大小$K_h$控制。因此，单层小的核卷积是不可能收集长距离信息的。为了解决香草卷积的这一缺点，我们提出了具有全局接受野的ParC。

3.1.2 ParC: Positional-Aware Circular Convolution

定义$w=w_0,w_1，\dots ，w_{K_h-1}$为核权值，$pe=p{e}_0,p{e}_1，\dots ，p{e}_{K_h-1}$为位置嵌入。对应图2,ParC可描述为:

这里$I=0,1，\dots ，h-1$。w为固定大小的可学习内核(由超参数指定)，$w_H$为调整后的可学习内核，其大小与相应的输入特征映射大小相匹配。PE为位置嵌入。这里我们采用插值函数f(·，N)(如双线性，双立方)来适应核的大小和位置嵌入(从$K_h$到H)， mod表示取模运算。

与常规卷积相比，ParC算子有四个主要的区别:1)全局核;2)圆卷积;3)位置嵌入;4)一维分解。为了有效地提取全局特征，这些设计都是必不可少的，这将在后面4.4节的烧蚀实验中得到证明。下面，我们将详细阐述这些设计差异的原因:

Global kernel and Circular Convolution.

为了提取整个输入映射的全局关系，ParC采用全局核，全局核的大小与对应特征映射的大小相同，记为$K_h=H$或$K_w=W$。在一些体系结构中，这在每个阶段都缩小了一半。例如在ResNet50或ConvNeXt中，四个阶段的特征分辨率分别为[56,28,14,7]。但是单纯地扩大普通卷积核本身的大小并不能有效地提取全局关系。由于使用了零填充，即使内核大小增加到分辨率，内核权重也将与零填充对齐，这除了绝对位置外不能提供有用的信息。当核与图像的边缘对齐时，这种效应发生得最为严重——对于二维卷积，3/4的输入实际上是零。因此，我们额外提出使用圆卷积。在进行圆卷积时，滑动窗口时，核权始终与有效像素对齐，如图2所示。

**Positional Embedding. **

正如前面的工作[48]所总结的，香草卷积可以在使用零填充时对位置信息进行编码。而循环卷积对输入图像进行周期性重用，会丢失部分位置信息。为了克服这个问题，我们引入了可学习的位置编码，插入到圆卷积之前。在接下来的实验中，我们证明了这对模型的性能非常重要，特别是对于对空间信息敏感的下游任务。

1D Decomposition

最后，为了保证模型尺寸和计算的可接受成本。我们将二维卷积和位置编码分为H(水平)和V(垂直)方向，这将参数和FLOPs的数量从O(H × W)减少到O(H + W)，这是一个相当大的压缩，当分辨率较大时。

**Implementation of Circular Convolution. **

从概念上讲，圆卷积需要与普通卷积分开实现，因为在计算卷积像素的索引时需要额外的模op。实际上，在调用普通的一维卷积例程之前，通过使用’ concat '函数填充输入特征映射，可以很容易地实现它(参见算法1)。

当考虑垂直维度W和通道维度C时，式2可扩展为

$\forall i\in [0,H-1]，\forall j\in [0,W-1]和\forall c\in [0,c-1]$，这是通道c的一层深度ParC-H的完整表示，输入分辨率为H×W。在ResNet50ParC中，我们也将每通道的ParC扩展到它的密集对应部分，重新引入通道相互作用，可以表示为:

considering $\forall i\in [0,H-1],\forall j\in [0,W-1],\forall c_i\in [0,C_{i-1}]$ and $\forall c_o\in [0,C_o-1]$.

3.2 Fast-ParC: Speed up ParC with its FFT Equivalent

Form

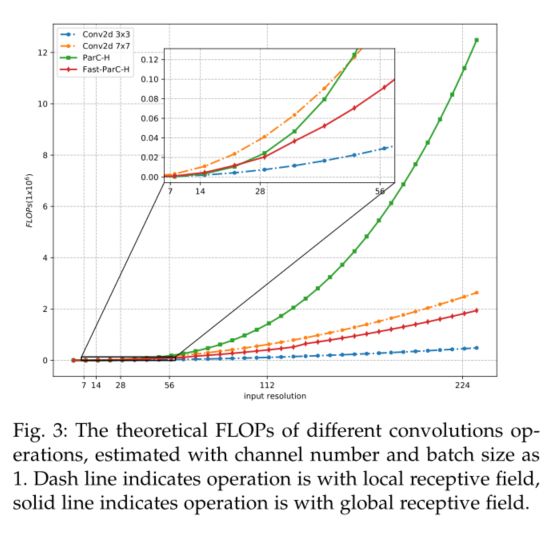
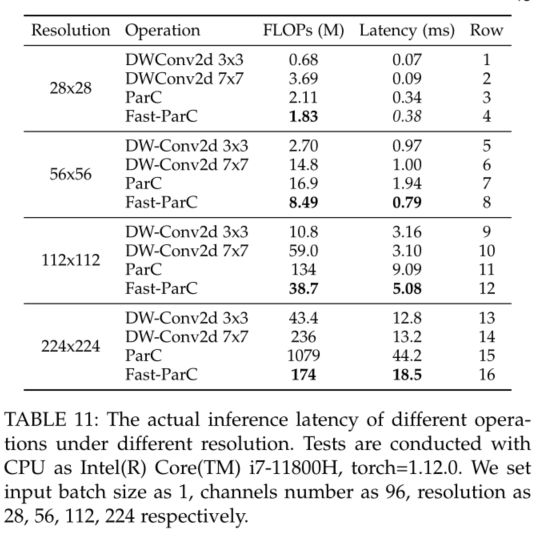
如图3所示，当特征分辨率较小时(如7×7)，应用ParC可以有效提取全局特征，降低计算复杂度。但是随着输入分辨率的增长，ParC的复杂度迅速超过了7×7卷积。为了克服这个问题，我们提出了一个名为Fast-ParC的ParC加速版本。当特征分辨率较大时(例如56×56)， Fast-ParC比ParC更有效。事实上，Fast-ParC在具有全局提取能力的同时，在较宽的分辨率区间内甚至比7×7卷积更高效。

我们在快速傅里叶变换(FFT)的帮助下推导出了快速parc。众所周知，FFT[50]可以简化线性卷积运算。但根据卷积定理[50]，对于离散信号，傅里叶域中的点积更接近于空间域中的圆卷积。这正是ParC与普通卷积的显著区别之一。此外，ParC的其他两个特性，全局核和右填充，也很好地符合傅里叶域的默认卷积模式。这个有趣的事实允许我们为ParC开发一个非常整洁和漂亮的频域实现。定义$x(n)，w(n)，y(n)$为时域的输入、权值和输出序列，$x(k)，w(k)，y(k)$为傅里叶域中的序列，可以得到如下等价关系:

Eq. 5给出了两个严格等价的数学表达式。空间域的ParC需要卷积式的运算，而在傅里叶域中则变成了简单的元乘法运算。在此基础上，我们提出了ParC运算的傅里叶域版本，称为Fast-ParC。从理论上可以证明Fast-ParC在空间域上与ParC是严格等价的(见附录A.1)。这两个实现之间的误差可以忽略不计。我们可以选择适当的实现根据实际使用的平台，分别用于训练和推断。这为ParC提供了强大的灵活性。算法1给出了伪代码。Fast-ParC的优势很明显:

首先，长度为N的一维- fft的乘法复杂度仅为O(N logN)，而空间域的一维卷积则需要$O(n^2)$。

由表1可知，当N较大时，空间卷积的复杂度大大超过基于fft的卷积。ParC采用全局核和圆卷积，与傅里叶卷积的默认空间格式相匹配。对于下游任务，如多实例的检测或分割，通常需要更高的分辨率。例如，对于COCO[51]，通常用于测试的分辨率是1280×800，对于ADE20k[52]是2048×512。当N较大时，Fast-ParC可以节省模型的flop，并获得更好的加速度。Fast-ParC还允许我们在计算预算可接受的较浅阶段使用ParC。这对于在新的体系结构[53]中实现ParC是必要的。

另一个优势实际上来自于FFT的软件/硬件支持。

由于FFT是一种经典的信号处理算法，许多平台对其加速都有现成的支持。当ParC应用于FPGA等定制平台时，可以有效利用片上DSP、预设计IP核等多种资源。此外，通用计算平台也有开箱即用的工具包(如CPU: torch)。FFT [54]， numpy .fft [55];GPU: cuFFT[56])。Fast-ParC的灵活性使我们能够根据不同的标准(例如，最大吞吐量，最小内存占用)，以及根据不同计算平台对算法的实际偏好，选择更好的实现。

幸运的是，Fast-ParC完全等同于ParC，而且替换不需要任何额外的转换。我们可以根据平台的要求选择ParC的具体实现形式。由于ParC和Fast-ParC具有最高的灵活性，用于训练和推断的实现也可以解耦。进一步探索基于FFT的其他高效卷积运算也是很有前途的方向，我们把这个问题留给未来。

3.3 Applying ParC on ViTs and ConvNets

为了验证ParC作为即插即用元操作器的有效性，我们基于3.1节中提出的操作构建了一系列基于ParC的模型。在这里，基线模型包括vit和ConvNets。具体来说，对于ViTs，选择MobileViT[11]作为基线，因为它在最近提出的轻型混合结构中实现了最佳的参数/精度权衡。采用ResNet50[28]、MobileNetv2[14]、ConvNext[27]作为ConvNet基线。ResNet50是实际应用中应用最广泛的模型。MobileNetV2是移动设备中最流行的模型。ConvNext是第一个保留了纯ConvNet架构，同时集成了vit的一些特性的ConvNet。我们在这里采用的四个模型都是具有代表性的。

3.3.1 ParC-ViTs

ParC-MetaFormer块。如图4和图5所示，ConvNets和vit在外层结构上存在较大差异。vit一般采用元前块作为基本体系结构。为了在vit中应用ParC算子，我们设计了ParC- metaformer块，用它来代替vit中的变压器块。

采用类似MetaFormer的结构。MetaFormer[49]块是vit最常使用的块结构，它通常由两个块序列组成组件:令牌混合器和通道混合器。这两个组件都使用残余结构。我们采用ParC作为令牌混合器来构建ParC- metaformer块。我们这样做是因为ParC可以从全局空间中提取全局特征和像素之间的交互信息，满足token mix模块的要求。与自我注意的复杂度是二次的不同，ParC的计算效率要高得多。用ParC替换这部分可以显著降低计算成本。在parparmetaformer Block中，我们采用了ParC-H和ParC-V的串行结构。考虑到对称性，有一半通道先通过ParC-H，另一半通道先通过ParC-V(如图4所示)。

添加通道时要注意通道混合器部分。尽管ParC保持了全局接受域和位置嵌入，vit相对于ConvNets的另一个优点是数据驱动。在ViTs中，自注意模块可以根据输入自适应权重。这使得vit成为数据驱动的模型，它可以专注于重要的特性并抑制不必要的特性，从而带来更好的性能。先前的文献[57] 58] [59]已经解释了保持模型数据驱动的重要性。用提出的全局圆卷积代替自注意，得到了一个能提取全局特征的纯卷积网络。但被取代的模型不再是数据驱动的。为了补偿，我们将通道明智注意模块插入通道混频器部分，如图4所示。在SENet[57]之后，我们首先通过全局平均池对输入特征$x\in R^{c\times h\times w}$的空间信息进行聚合，得到聚合特征$x_a\in R^{c\times 1\times 1}$，然后将$x_a$输入到多层感知中，生成通道wise权重$a\in R^{c\times 1\times 1}$，将a与x通道wise相乘，生成最终输出。

MobieViT-ParC Network.

目前，现有杂化构造基本可分为三种主要构造，分别为串联构造[25] [42]、平行构造[12]和分叉构造[11] [24]。在这三种结构中，第三种结构目前性能最好。MobileViT[11]也采用了分叉结构。受此启发，我们基于MobileViT构建了我们的分岔结构模型。MobileViT由两大类模块组成。浅阶段由MobileNetV2块组成，有局部感受野。深段由ViT区块组成，具有全局接受野。我们保留所有的MobileNetV2块，并用相应的ParC块替换所有的ViT块。该替换将混合结构模型转换为纯ConvNet模型，同时保留了其全局特征提取能力。

3.3.2 ParC-ConvNets

对于ParC-ConvNets，我们专注于为ConvNets提供全局接受域。用ParC运算代替香草卷积(如图5 (a)所示)，我们构建了不同的基于ParC的块(如图5 (b)©(d)所示)。以往的混合结构工作[25] [42] [11]也得出了类似的结论:早期阶段采用局部提取块，深部阶段采用全局提取块的模型性能最好。由于ParC拥有全局接受域，我们按照此规则将基于ParC的块插入到ConvNets中(如图5 (e)所示)。

ParC BottleNeck and ResNet50-ParC Network.

ResNet[28]是最经典的ConvNet之一。简单地用ParC算子替换原来ResNet50瓶颈的3×3卷积，我们就可以得到ParC瓶颈(见图5 (b))。由于ParC-H和ParCV的特性可能存在显著差异，因此它们之间不存在通道相互作用。这类似于采用group=2的组卷积[60]。ResNet的主体部分可分为4个阶段，每个阶段由一对重复的瓶颈块组成。具体来说，ResNet50在四个阶段分别有[3,4,6,3]块。用ParC瓶颈替换ResNet50倒数第二段的最后1/2和最后一段的最后1/3，得到ResNet50-ParC。

ParC-MobileNetV2 Block and MobileNetV2-ParC Net-work.

MobileNetV2[14]是轻量级模型的典型代表。通过将倒置瓶颈中的3×3深度卷积替换为深度ParC，我们得到了ParC- mobilenetv2块(见图5 ©)。MobileNetV2比Resnet50更薄、更深，7级的区块数量分别为[1、2、3、4、3、1]。用ParC-MobileNetV2块替换stage 4的最后1/2块和stage[5,6]的最后1/3块可以得到MobilenetV2-ParC。

ParC-ConvNeXt Block and ConvNeXt-ParC Network.

ConvNeXt[27]对原ResNet50结构进行了一系列的修改，向变压器学习。在此期间，3×3卷积将被7×7深度卷积替换。这扩大了局部的接受域，但仍不能对全局信息进行分级。我们进一步用深度ParC代替ConvNeXt Block中的7×7深度卷积。这样我们就得到了ParC-ConvNeXt块(见图5 (d))。将ConvNeXt最后两个阶段的最后1/3块替换为ParC-ConvNeXt块，得到了一个ConvNeXtParC示例。我们将ConvNeXt-T中的基本通道数减少到48个(即每个级[48,96,192,384])，从而得到轻量级的ConvNeXt-XT，这在部署在边缘计算设备上更受欢迎，并且具有更短的实验周期。

需要注意的是，在ParC-MetaFormer中，采用了ParC-H和ParC-W的序列，使接受场与自我注意保持一致，因为这种设计是用来取代自我注意的。在ParC- convnets中，我们采用了ParC H和ParC- v的并行(每一层)，如图5所示。根据实验结果，这种设置已经可以提供足够的性能增益相对于传统的ConvNets。事实上，由于我们不只是使用一个ParC-ConvNet块，ParC-ConvNet仍然具有全局接受野。

4 EXPERIMENT

5 DISCUSSION

在本节中，我们首先分析了香草卷积和ParC学习到的权值的空间分布。在此基础上，进一步说明它们仍然学习相似的特征提取模式。

此外，我们还提供了两种常用的可视化方案，有效接受域(ERF)[15]和grada - cam[29]的结果，以分析ParC的机制。结果表明，基于parc的模型即使在高分辨率下也能获得全局特征，这使得模型在获取实例相关语义信息时更加全面。

6 CONCLUSION

我们设计了一个新的即插即用算子ParC(位置感知圆形卷积)。ParC具有像ViT中的自我注意一样的全局接受域，但由于采用纯卷积运算，不同的硬件平台可以更方便地支持它。我们证明了它提高了网络的分类性能，无论是插入到基于变压器的网络还是基于卷积的网络。此外，基于parcel的模型在处理下游任务时也具有优势。分析了其内部机制及其与普通大核卷积的区别，并对其优越性给出了令人信服的解释。为了在大分辨率条件下应用ParC，还提出了基于ffc的快速ParC。快速ParC操作能够在高输入分辨率的情况下保持较低的计算预算，使ParC成为大多数计算机视觉任务具有竞争力的通用选择。