【菜菜的sklearn课堂笔记】决策树-决策树的优缺点 & 分类树在合成数集上的表现

视频作者：菜菜TsaiTsai
链接：【技术干货】菜菜的机器学习sklearn【全85集】Python进阶_哔哩哔哩_bilibili

决策树的优缺点

决策树优点

1. 易于理解和解释，因为树木可以画出来被看见
2. 需要很少的数据准备。其他很多算法通常都需要数据规范化，需要创建虚拟变量并删除空值等。但请注意， sklearn中的决策树模块不支持对缺失值的处理。
3. 使用树的成本（比如说，在预测数据的时候）是用于训练树的数据点的数量的对数，相比于其他算法，这是一个很低的成本。

个人理解，对于一个树模型，假设有n级，那么我们树木的结点数目最大为$2^{n-1}$，对于一个新的样本，我们要预测其标签，我们就需要判断$n-1$次
$$n-1=\log 2^{n-1}$$
这就是为什么说使用树的成本是用于训练树的数据点的数量的对数

5. 能够同时处理数字和分类数据，既可以做回归又可以做分类。其他技术通常专门用于分析仅具有一种变量类型的数据集。

类DecisionTreeClassifier和DecisionTreeRegressor
分类树是根据叶结点处所含样本的标签的多数类来决定该叶结点的标签
回归树可以认为是根据叶结点处所含样本的均值来决定该叶结点的标签

7. 能够处理多输出问题，即含有多个标签的问题，注意与一个标签中含有多种标签分类的问题区别开

个人理解，多个标签指输入的Y为多列，即多标签问题；一个标签中含有多种标签值输入的Y为一列，但是这一列的取值有多种，即单标签多分类问题，对应的是二分类问题

9. 是一个白盒模型，结果很容易能够被解释。如果在模型中可以观察到给定的情况，则可以通过布尔逻辑轻松解释条件。相反，在黑盒模型中（例如，在人工神经网络中），结果可能更难以解释。
10. 可以使用统计测试验证模型，这让我们可以考虑模型的可靠性。
11. 即使其假设在某种程度上违反了生成数据的真实模型，也能够表现良好。

决策树的缺点

1. 决策树学习者可能创建过于复杂的树，这些树不能很好地推广数据。这称为过度拟合。修剪，设置叶节点所需的最小样本数或设置树的最大深度等机制是避免此问题所必需的，而这些参数的整合和调整对初学者来说会比较晦涩
2. 决策树可能不稳定，数据中微小的变化可能导致生成完全不同的树，这个问题需要通过集成算法来解决。
3. 决策树的学习是基于贪婪算法，它靠优化局部最优（每个节点的最优）来试图达到整体的最优，但这种做法不能保证返回全局最优决策树。这个问题也可以由集成算法来解决，在随机森林中，特征和样本会在分枝过程中被随机采样。

2、3都被集成算法很好的解决，也就是后面要讲的随机森林算法

4. 有些概念很难学习，因为决策树不容易表达它们，例如XOR，奇偶校验或多路复用器问题。
5. 如果标签中的某些类占主导地位，决策树学习者会创建偏向主导类的树。因此，建议在拟合决策树之前平衡数据集。

可以考虑上采样（？）或者调整class_weight

分类树在合成数集上的表现

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons,make_circles,make_classification
from sklearn.tree import DecisionTreeClassifier

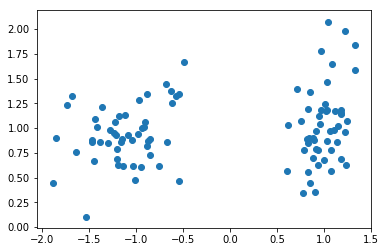
X, y = make_classification(n_samples=100
                          ,n_features=2
                          ,n_redundant=0
                          ,n_informative=2
                          ,random_state=1
                          ,n_clusters_per_class=1)
plt.scatter(X[:,0],X[:,1])

关于make_classification

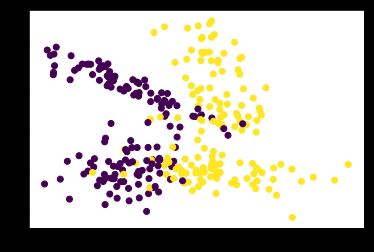
X, y = make_classification(n_samples=300
                          ,n_features=2
                          ,n_redundant=0
                          ,n_informative=2
                          ,random_state=1
                          ,n_clusters_per_class=2)
plt.scatter(X[:,0],X[:,1],c=y)
# n_clusters_per_class每个类的集群数
# n_features：int，默认20，特征总数。这些包括n_informative 信息特征、n_redundant冗余特征、 n_repeated重复特征和 n_features-n_informative-n_redundant-n_repeated随机抽取的无用特征。
# n_informative：int，默认2，信息特征的数量。
# n_redundant：int，默认2，冗余特征的数量。这些特征是作为信息特征的随机线性组合生成的。(假设n_informative=F1,F2,…那么n_redundant= aF1+bF2+… a,b,c就是随机数)
# n_repeated：int，默认0，从信息特征和冗余特征中随机抽取的重复特征的数量。
# n_classes：int，默认2，分类问题的类（或标签）数。
# 关于冗余特征好像有个叫mRMR算法的，不太了解

链接：make_classification函数_BlackStar_L的博客-CSDN博客_make_classification

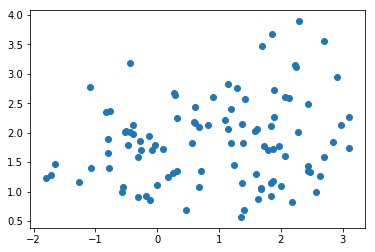
从图上可以看出，生成的二分型数据的两个簇离彼此很远，这样不利于我们测试分类器的效果，因此我们生成随机数组，通过让已经生成的二分型数据点加减0~1之间的随机数，使数据分布变得更散更稀疏

注意，这个过程只能够运行一次，因为多次运行之后X会变得非常稀疏，两个簇的数据会混合在一起，分类器的效应会继续下降

rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
# 加0~2之间的随机数
# uniform(low,high,size)，从一个均匀分布[low,high)中随机采样
# 默认low=0，high=1
linearly_separable = (X,y)

plt.scatter(X[:,0],X[:,1])

datasets = [make_moons(noise=0.3,random_state=0)
           ,make_circles(noise=0.2,factor=0.5,random_state=1)
           ,linearly_separable]

画出三种数据集和三棵决策树的分类效应图像

figure = plt.figure(figsize=(6,9))
# figsize中的元组第一个6对应列宽，第二个9对应行高
i = 1
# 设置用来安排图像显示位置的全局变量i

for ds_index, ds in enumerate(datasets):
    X,y = ds
    # 对X中的数据进行标准化处理，然后分训练集和测试集
    # 决策树不进行数据标准化应该也没什么问题，而且数据标准化后会让取值更难解释
    X = StandardScaler().fit_transform(X)
    X_train,X_test,Y_train,Y_test = train_test_split(X,y,test_size=0.4,random_state=42)
    
    X1_min, X1_max = X[:,0].min() - 0.5, X[:,0].max() + 0.5
    X2_min, X2_max = X[:,1].min() - 0.5, X[:,1].max() + 0.5
    
    array1,array2 = np.meshgrid(np.arange(X1_min,X1_max,0.2)
                               ,np.arange(X2_min,X2_max,0.2))
    # array1可以看做一行横坐标纵向复制铺满一个矩阵，从负到正
    # array2可以看做一列纵坐标横向复制铺满一个矩阵，从负到正
    
    # 用ListedColormap为画布创建颜色，#FF0000正红，#0000FF正蓝
    cm = plt.cm.RdBu
    cm_bright = ListedColormap(['#FF0000','#0000FF'])
    
    ax = plt.subplot(len(datasets),2,i)
    # 在画布上加上一个子图，数据为len(datasets)行，2列，放在位置i上
    # i的取值对于整个画布，从左到右，从上到下，一行一行的向下增加
    # subplots和subplot。两者都可以实现画子图功能，只不过subplots帮我们把画板规划好了，并且创建时可以直接指定画板的大小，返回画布对象和坐标数组对象。而subplot是在已经创建好的画布上增加子图，每次只能返回一个坐标对象。
    
    if ds_index == 0:
        ax.set_title("Input data")
    
    ax.scatter(X_train[:,0],X_train[:,1],c=Y_train,cmap=cm_bright,edgecolors='k')
    ax.scatter(X_test[:,0],X_test[:,1],c=Y_test,cmap=cm_bright,edgecolors='k',alpha=0.6)
    # 其实基本区分不出测试集的点hhhh
    # 为图设置坐标轴的最大值和最小值，并设定没有坐标轴
    ax.set_xlim(array1.min(),array1.max())
    ax.set_ylim(array2.min(),array2.max())
    ax.set_xticks(())
    ax.set_yticks(())
    
    # 每次循环之后，改变i的取值让图每次位列不同的位置
    i += 1
    
    ax = plt.subplot(len(datasets),2,i)
    # 在函数最开始，我们定义了i=1，并且在上边建立数据集的图像的时候，已经让i+1，所以i在这里每次循环中的取值为2,4,6
    
    clf = DecisionTreeClassifier(max_depth=5,random_state=1) # 也有随机性
    clf.fit(X_train,Y_train)
    score = clf.score(X_test,Y_test)
    
    Z = clf.predict_proba(np.c_[array1.ravel(),array2.ravel()])[:,1]
    # np.c_[array1.ravel(),array2.ravel()]返回的就是坐标点
    # np.c_是能够将两个数组组合起来的函数
    # 从左下，到右下，然后一行一行的从左向右往上走
    Z = Z.reshape(array1.shape)
    
    ax.contourf(array1,array2,Z,cmap=cm,alpha=0.8)
    # 将返回的类概率作为数据，放到contourf里面绘制去绘制轮廓
    # 这里我们指定levels是没有意义的，如果查看Z会发现，任何一个维度的所有数据只有两个取值，即0,1
    # 所以说如果我们使用contour，因为无法指定level就没有意义了
    # 如果使用contour配合pcolormesh着色，但是要指定Z的范围，交界处依然会有问题，所以考虑使用contourf
    # 相比于contour，contourf本身就会对不同区域进行着色
    # 实际上predict_proba返回的不只是0,1，根据定义它可以返回[0,1]
    # 只是因为这里样本太少，导致生成的决策树每个叶结点上恰好只有一类样本，所以返回值只有0,1
    
    ax.scatter(X_train[:,0],X_train[:,1],c=Y_train,cmap=cm_bright,edgecolors='k')
    ax.scatter(X_test[:,0],X_test[:,1],c=Y_test,cmap=cm_bright,edgecolors='k',alpha=0.6)
    ax.set_xlim(array1.min(),array1.max())
    ax.set_ylim(array2.min(),array2.max())
    ax.set_xticks(())
    ax.set_yticks(())
    
    if ds_index == 0:
        ax.set_title("Decision Tree")
    
    # 写在右下角的数字
    ax.text(array1.max() - 0.3,array2.min() + 0.3
           ,("{:.1f}%").format(score*100)
           ,size=15
           ,horizontalalignment='right')
    
    # 让i继续加一
    i += 1
    
plt.tight_layout()
plt.show()

很容易看得出，分类树天生不擅长环形数据。每个模型都有自己的决策上限，所以一个怎样调整都无法提升表现的可能性也是有的。当一个模型怎么调整都不行的时候，我们可以选择换其他的模型使用。

最擅长月亮型数据的是最近邻算法，RBF支持向量机和高斯过程；最擅长环形数据的是最近邻算法和高斯过程；最擅长对半分的数据的是朴素贝叶斯，神经网络和随机森林。