自己对粒子群算法的理解（附matlab直接运行代码)(二维)

               首先声明，作者为准大二学生，由于一些特殊原因被某研究生老师拉近了一个研究组，为了更好地记忆和复习，所以写了一下内容，如有错误，希望提出，直接骂我都可以。

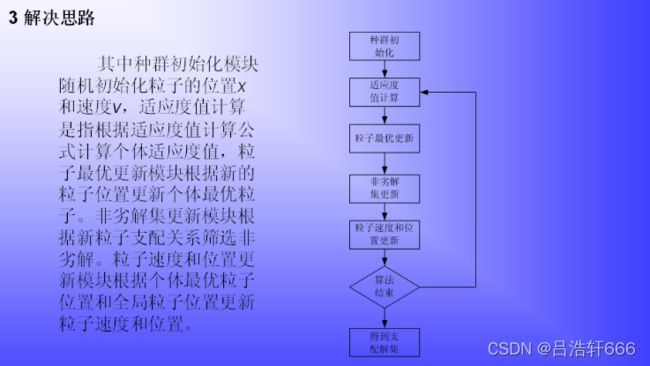
现在开始正文，首先老样子，介绍一下粒子群算法的定义。

①定义（原理）

粒子群算法(PSO)是由Kennedy 和Eberhart等于1995 年开发的一种演化计算技术, 来源于Millonas 对一个简化社会模型的模拟。

其中“群( swarm )”来源于粒子群符合在开发应用于人工生命(artificiallife) 的模型时所提出的群体智能的5个基本原则。而“粒子(particle)”则是一个折衷的选择，因为既需要将群体中的成员描述为没有质量、没有体积的，同时也需要描述它的速度和加速状态。

由于PSO 算法概念简单，实现容易，短短几年时间，PSO 算法便获得了很大的发展，并在一些领域得到应用。

PSO 模拟鸟群的捕食行为。一群鸟在随机搜索食物，在这个区域里只有一块食物。所有的鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢。最简单有效的就是搜寻目前离食物最近的鸟的周围区域。 PSO 从这种模型中得到启示并用于解决优化问题。

PSO 中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitness value)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。 PSO 初始化为一群随机粒子(随机解)，然后通过迭代找到最优解，在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值 p Best，另一个极值是整个种群目前找到的最优解，这个极值是全局极值 g Best。另外也可以不用整个种群而只是用其中一部分最优粒子的邻

居，那么在所有邻居中的极值就是局部极值。

在每一次迭代过程中，粒子通过个体极值和群体极值更新自身的速度和位置，更新公式如下:

PSO 算法与其他演化算法相似, 也是基于群体的, 根据对环境的适应度将群体中的个体移动到好的区域，然而它不像其他演化算法那样对个体使用演化算子, 而是将每个个体看作n维搜索空间中的一个没有体积的微粒(点)，在搜索空间中以一定的速度飞行。这个速度根据它本身的飞行经验以及同伴的飞行经验进行动态调整。

其中：

W：惯性权重

r1 r2：分布于[0,1]区间的随机数；

k：是当前迭代次数

pk id :个体最优例子位置

pk gd：全局最优粒子位置

c1,c2:常数

V：粒子速度

X：粒子位置

②算法步骤（过程）

 发现了吗，PSO（粒子群算法）是不是有那么一点眼熟，是不是很像进化算法？他们都以随机的方式初始化了种群，都用适应值来评价了系统，都根据适应值来进行了一定的随机搜索，甚至都不能找到最优的解。

但差别还是很大的，PSO没有遗传操作（比如变异），它是依靠自己的运行速度来决定搜索。而且他不像遗传算法，粒子群算法是有记忆的。

在PSO中，只有的全局最优粒子位置（pBest）给出的信息给其他的例子，这是单向的信息流动。整个搜索更新过程是跟随当前最优解的过程。与进化算法比较，在大多数的情况下，所有的粒子可能更快的收敛于最优解。研究表明 PSO 是一种很有潜力的神经网络算法，同时 PSO 速度比较快而且可以得到比较好的结果。

但是！！，问题还是大大滴有，这类智能算法都不可避免的有陷入局部最优解的风险。

③PSO的MATLAB实现（以matlab为主）

基于粒子群算法的二维背包问题

首先还要先说一下多目标优化问题的原理，毕竟是写给自己看的，多写一点，忘了也

方便理解。要看代码的直接往下滑就好。

        多目标问题显著特点是优化各个目标使其达到综合的最优值。然而，由于多目标优化问题的

各个目标之间往往是相互冲突的，在满足其中一个目标最优的同时，其他的目标往往可能

会受其影响变差。所以一般适用于单目标问题的方法难以用于多目标问题的求解。

        多目标优化问题求解中的重要概念就是非劣解和非劣解集，

非劣解：在多目标优化问题的可行域中存在一个问题解，不存在另一个可行解，使得一个解中的目标全部劣于该解，则称该解为多目标优化问题的非劣解。说白了就是不是最差的那个解

非劣解集：所有非劣解的集合叫做非劣解集

下面就是运用标准粒子群算法求解多目标背包问题的步骤

 

 

 

  

main.m

%% 该函数演示多目标perota优化问题
%清空环境
clc
clear
%load data
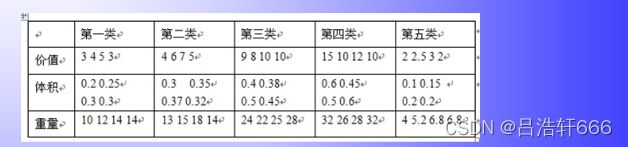
P = [3 4 9 15 2;4 6 8 10 2.5;5 7 10 12 3;3 5 10 10 2]
R = [0.2 0.3 0.4 0.6 0.1;0.25 0.35 0.38 0.45 0.15;0.3 0.37 0.5 0.5 0.2;0.3 0.32 0.45 0.6 0.2]
C = [10 13 24 32 4;12 15 22 26 5.2;14 18 25 28 6.8;14 14 28 32 6.8]

%% 初始参数
objnum=size(P,1); %类中物品个数
weight=92;        %总重量限制
%初始化程序
Dim=5;     %粒子维数
xSize=50;  %种群个数

%下面这五个参数是要自己设置的，为什么c1=c2=1.497,因为我之前在别人的一篇论文里见过说是取1.497的时候效果最好，最大速度通常设定为粒子的范围宽度。将c1和c2统一为一个控制参数φ=c1+c2。当φ=4.1时具有良好的收敛效果。
ω=0.7298和c1=c2=1.497时算法有较好的收敛性能。
MaxIt=200; %迭代次数
c1=1.497;    %算法参数
c2=1.497;    %算法参数 
wmax=1.2;  %惯性因子
wmin=0.1;  %惯性因子

x=unidrnd(4,xSize,Dim);  %粒子初始化
v=zeros(xSize,Dim);      %速度初始化

xbest=x;           %个体最佳值
gbest=x(1,:);      %粒子群最佳位置

% 粒子适应度值 
px=zeros(1,xSize);   %粒子价值目标
rx=zeros(1,xSize);   %粒子体积目标
cx=zeros(1,xSize);   %重量约束

% 最优值初始化
pxbest=zeros(1,xSize); %粒子最优价值目标
rxbest=zeros(1,xSize); %粒子最优体积目标
cxbest=zeros(1,xSize);  %记录重量，以求约束

% 上一次的值
pxPrior=zeros(1,xSize);%粒子价值目标
rxPrior=zeros(1,xSize);%粒子体积目标
cxPrior=zeros(1,xSize);%记录重量，以求约束

%计算初始目标向量
for i=1:xSize
    for j=1:Dim %控制类别
        px(i) = px(i)+P(x(i,j),j);  %粒子价值
        rx(i) = rx(i)+R(x(i,j),j);  %粒子体积
        cx(i) = cx(i)+C(x(i,j),j);  %粒子重量
    end
end
% 粒子最优位置
pxbest=px;rxbest=rx;cxbest=cx;

%% 初始筛选非劣解
flj=[];
fljx=[];
fljNum=0;
%两个实数相等精度
tol=1e-7;
for i=1:xSize
    flag=0;  %支配标志
    for j=1:xSize  
        if j~=i
            if ((px(i)rx(j))) ||((abs(px(i)-px(j))rx(j)))||((px(i)weight) %哦按段支配关系
                flag=1;
                break;
            end
        end
    end
    
    %判断有无被支配/是否被支配构建新结集 
    if flag==0
        fljNum=fljNum+1;
        % 记录非劣解
        flj(fljNum,1)=px(i);flj(fljNum,2)=rx(i);flj(fljNum,3)=cx(i);
        % 非劣解位置
        fljx(fljNum,:)=x(i,:); 
    end
end

%% 循环迭代
for iter=1:MaxIt
    
    % 权值更新
    w=wmax-(wmax-wmin)*iter/MaxIt;
    
    %从非劣解中选择粒子作为全局最优解
    s=size(fljx,1);       
    index=randi(s,1,1);  
    gbest=fljx(index,:);

    %% 群体更新
    for i=1:xSize
        %速度更新
        v(i,:)=w*v(i,:)+c1*rand(1,1)*(xbest(i,:)-x(i,:))+c2*rand(1,1)*(gbest-x(i,:));
        
        %位置更新
        x(i,:)=x(i,:)+v(i,:);
        x(i,:) = rem(x(i,:),objnum)/double(objnum);
        index1=find(x(i,:)<=0);
        if ~isempty(index1)
            x(i,index1)=rand(size(index1));
        end
        x(i,:)=ceil(4*x(i,:));        
    end
    
    %% 计算个体适应度
    pxPrior(:)=0;
    rxPrior(:)=0;
    cxPrior(:)=0;
    for i=1:xSize
        for j=1:Dim %控制类别
            pxPrior(i) = pxPrior(i)+P(x(i,j),j);  %计算粒子i 价值
            rxPrior(i) = rxPrior(i)+R(x(i,j),j);  %计算粒子i 体积
            cxPrior(i) = cxPrior(i)+C(x(i,j),j);  %计算粒子i 重量
        end
    end
    
    %% 更新粒子历史最佳
    for i=1:xSize
        %现在的支配原有的，替代原有的
         if ((px(i)rxPrior(i))) ||((abs(px(i)-pxPrior(i))rxPrior(i)))||((px(i)weight) 
                xbest(i,:)=x(i,:);%没有记录目标值
                pxbest(i)=pxPrior(i);rxbest(i)=rxPrior(i);cxbest(i)=cxPrior(i);
          end
        
        %彼此不受支配，随机决定
        if ~( ((px(i)rxPrior(i))) ||((abs(px(i)-pxPrior(i))rxPrior(i)))||((px(i)weight) )...
                &&  ~( ((pxPrior(i)rx(i))) ||((abs(pxPrior(i)-px(i))rx(i)))...
                ||((pxPrior(i)weight) )
            if rand(1,1)<0.5
                xbest(i,:)=x(i,:);
                  pxbest(i)=pxPrior(i);rxbest(i)=rxPrior(i);cxbest(i)=cxPrior(i);
            end
        end
    end

    %% 更新非劣解集合
    px=pxPrior;
    rx=rxPrior;
    cx=cxPrior;
    %更新升级非劣解集合
    s=size(flj,1);%目前非劣解集合中元素个数
   
    %先将非劣解集合和xbest合并
    pppx=zeros(1,s+xSize);
    rrrx=zeros(1,s+xSize);
    cccx=zeros(1,s+xSize);
    pppx(1:xSize)=pxbest;pppx(xSize+1:end)=flj(:,1)';
    rrrx(1:xSize)=rxbest;rrrx(xSize+1:end)=flj(:,2)';
    cccx(1:xSize)=cxbest;cccx(xSize+1:end)=flj(:,3)';
    xxbest=zeros(s+xSize,Dim);
    xxbest(1:xSize,:)=xbest;
    xxbest(xSize+1:end,:)=fljx;
   
    %筛选非劣解
    flj=[];
    fljx=[];
    k=0;
    tol=1e-7;
    for i=1:xSize+s
        flag=0;%没有被支配
        %判断该点是否非劣
        for j=1:xSize+s 
            if j~=i
                if ((pppx(i)rrrx(j))) ||((abs(pppx(i)-pppx(j))rrrx(j)))||((pppx(i)weight) %有一次被支配
                    flag=1;
                    break;
                end
            end
        end

        %判断有无被支配
        if flag==0
            k=k+1;
            flj(k,1)=pppx(i);flj(k,2)=rrrx(i);flj(k,3)=cccx(i);%记录非劣解
            fljx(k,:)=xxbest(i,:);%非劣解位置
        end
    end
    
    %去掉重复粒子
    repflag=0;   %重复标志
    k=1;         %不同非劣解粒子数
    flj2=[];     %存储不同非劣解
    fljx2=[];    %存储不同非劣解粒子位置
    flj2(k,:)=flj(1,:);
    fljx2(k,:)=fljx(1,:);
    for j=2:size(flj,1)
        repflag=0;  %重复标志
        for i=1:size(flj2,1)
            result=(fljx(j,:)==fljx2(i,:));
            if length(find(result==1))==Dim
                repflag=1;%有重复
            end
        end
        %粒子不同，存储
        if repflag==0 
            k=k+1;
            flj2(k,:)=flj(j,:);
            fljx2(k,:)=fljx(j,:);
        end
        
    end
    
    %非劣解更新
    flj=flj2;
    fljx=fljx2;

end

%绘制非劣解分布
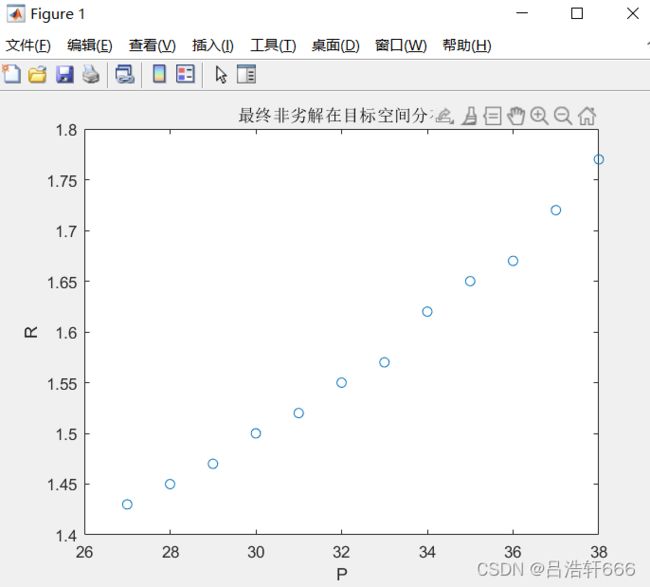
plot(flj(:,1),flj(:,2),'o') 
xlabel('P')
ylabel('R')
title('最终非劣解在目标空间分布')
disp('非劣解flj中三列依次为P，R，C')

结果：

                                                           图一

                                                                         图二

        这边我要解释一下，用我自己的语言，我一开是学这个的时候纠结这个图特别久，老师配套的视频讲的又很不明白，一言难尽。

        有五类问题，每类选择一个放入背包，得到整体的解，因为解有很多，所以没有在图片中将

所有表示搞出来，由图二可以看出解面是一个解线，我们在求多目标的时候得到的不是单个最优解

而是得到一个解的集合（曲线），这里有个概念就是支配解，上面提过了这个，可以回去看。

         另外图二的看法其实很简单，就是每一个点代表一个总的价值：体积，重量没有在图中显示出来，当然也可以显示，不过没有必要，不难看出最终越来越逼近最优解了。

        下一篇博客我会写一下如何改进这个二维背包问题