粒子群算法matlab代码实例使用与参数解读（二维数据）

在网络中有很多的博客都已经粒子群算法的算法本质讲解的非常清晰明了，但是经本人在当初实际编程和使用中发现，对粒子群算法代码的实际使用还是存在着调参不便，适应度函数编辑不便等对新手较为不友好的现象，因此本文仅作于同样是小白的各位同学，以其达到交流学习的目的。

粒子群算法介绍

粒子群算法（也称粒子群优化算法（particle swarm optimization, PSO）），模拟鸟群随机搜索食物的行为。粒子群算法中，每个优化问题的潜在解都是搜索空间中的一只鸟，叫做“粒子”。所有的粒子都有一个由被优化的函数决定的适应值（fitness value），每个粒子还有一个速度决定它们“飞行”的方向和距离。

粒子群算法初始化为一群随机的粒子（随机解），然后根据迭代找到最优解。每一次迭代中，粒子通过跟踪两个极值来更新自己：第1个是粒子本身所找到的最优解，这个称为个体极值；第2个是整个种群目前找到的最优解，这个称为全局极值。也可以不用整个种群，而是用其中的一部分作为粒子的邻居，称为局部极值。

通过形象化的理解可以理解成在高低不平的山脉上有一个最低点的谷底藏着丰富的食物，一群鸟禽随机的分布在山脉的各个位置，所有鸟都不知道食物的方向，只知道据这些食物有多远，只能随机的进行寻找和移动，好在他们之间可以相互通讯并交换自己在距离食物最近的位置，当确认距离食物最近的鸟的位置后，所有的鸟群都会朝着这个方向搜索，但是在搜索过程中会发现有别的鸟路过距离食物更近的位置，这个时候为了让方向更加准确，就对两个位置进行矢量相加，最后确定新的搜索方向。

粒子群算法使用场景

再将粒子群简化一下，将整个算法封装成一个不知道的黑箱。
让我们关注一下输入和输出：
输入是一个关于因变量Y和自变量Xi（i=1，2，3…）的多元多次函数，或者可以理解为一份地图，或者一个下界的收敛曲线
而输出是这个函数使得函数因变量值最小，即这份地图或者曲线的最低点。

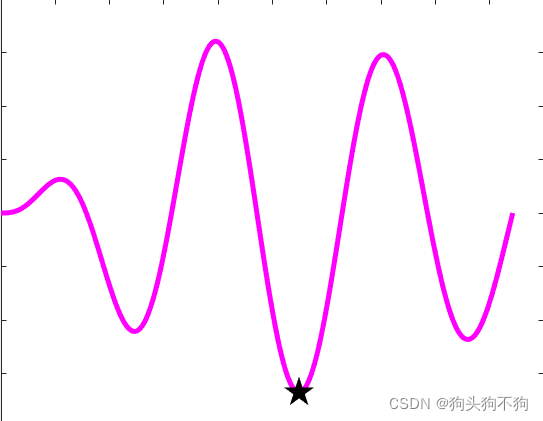
总而言之，粒子群算法是用于对一个有上界或者有下界的凸函数的最优极值位置的定位函数。

粒子群的优缺点

首先，粒子群算法的不需要大量调试参数，也因此成为了广大优化算法中最为流行的几种算法之一，其次粒子群算法是一种高效的并行搜索算法，有效的提高了算法复杂度，且其速度在实际操作中是优于遗传算法。

但是粒子群算法同样具有不足，比如易于陷入局部最优解，在后期收敛速度慢等问题，需要具体场合进行具体分析。

实例编程分析

假设我们已知加入水的量X与某化学试剂活性Y的关系函数：

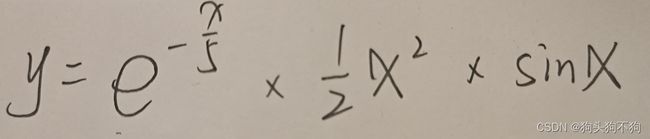
要求找到最合适的加水量X使得试剂活性Y最低

matlab代码如下

clc;
clear;
close all;

% 参数赋值
tic;                              
E0=0.001;                        
MaxNum=500;                    
narvs=1;                         
particlesize=100;                 
c1=3;                          
c2=2;                          
w=0.6;                         
vmax=0.8;                        
x=8*rand(particlesize,narvs);     
v=10*rand(particlesize,narvs);       


fitness = @(x)exp(-x./3).*sin(3.*x);		%定义适应度函数
f = zeros(1,particlesize);      % 预分配
for i=1:particlesize
    for j=1:narvs
        f(i)=fitness(x(i,j));
    end
end
personalbest_x=x;
personalbest_faval=f;
[globalbest_faval,i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:);
k=1;
while k<=MaxNum
    for i=1:particlesize
        for j=1:narvs
            f(i)=fitness(x(i,j));
        end
        if f(i)<personalbest_faval(i) 
            personalbest_faval(i)=f(i);
            personalbest_x(i,:)=x(i,:);
        end
    end
    [globalbest_faval,i]=min(personalbest_faval);
    globalbest_x=personalbest_x(i,:);
    for i=1:particlesize 
        v(i,:)=w*v(i,:)+c1*rand*(personalbest_x(i,:)-x(i,:))...
            +c2*rand*(globalbest_x-x(i,:));
        for j=1:narvs    
            if v(i,j)>vmax
                v(i,j)=vmax;
            elseif v(i,j)<-vmax
                v(i,j)=-vmax;
            end
        end
        x(i,:)=x(i,:)+v(i,:);
    end
    if abs(globalbest_faval)<E0,break,end
    k=k+1;
end
Value1=globalbest_faval-1; Value1=num2str(Value1);
disp(strcat('the min value','=',Value1));
%输出最优值所在的横坐标位置
Value2=globalbest_x; Value2=num2str(Value2);
disp(strcat('the corresponding coordinate','=',Value2));

x=0:pi/50:4*pi;     
y=exp(-x/3).*sin(3*x);

plot(x,y,'r-','linewidth',3);
hold on;

x = str2num(Value2);
y=exp(-x./3).*sin(3.*x);%定义适应度函数;
plot( globalbest_x ,y,'kp','linewidth',4);
legend('目标函数','搜索到的最小值');
xlabel('x');
ylabel('y');
grid on;
toc;

运行结果：

代码分析

在使用代码进行修改完成实例的过程中需要注意修改以下代码

fitness = @(x)exp(-x./3).*sin(3.*x);		%定义适应度函数

这部分的代码是定义需要进行寻优，及是需要找到极值的函数

[globalbest_faval,i]=min(personalbest_faval);

这里通过matlab自带的min函数和max函数确定是进行极大值寻优还是极小值寻优。

x=0:pi/50:4*pi;     
y=exp(-x/3).*sin(3*x);

这部分代码是根据自变量的范围进行曲线画图，在实际案例中，会出现自变量存在取值范围的问题，需要在代码中具体考虑

x = str2num(Value2);
y=exp(-x./3).*sin(3.*x);%定义适应度函数;
plot( globalbest_x ,y,'kp','linewidth',4);

这部分代码中，str2num(Value2)是在之前算法中已经找出的最有位置，及是使得试剂活性Y最低的加水量X，将它的值赋予x，并求取得到最低活性Y的值，在图上通过黑色的五角星进行标记

参数分析

tic;                              %程序运行计时
E0=0.001;                        %允许误差
MaxNum=500;                    %粒子最大迭代次数
narvs=1;                         %目标函数的自变量个数
particlesize=100;                    %粒子群规模
c1=3;                            %每个粒子的个体学习因子，也称为加速常数
c2=2;                            %每个粒子的社会学习因子，也称为加速常数
w=0.6;                           %惯性因子
vmax=0.8;                        %粒子的最大飞翔速度
x=8*rand(particlesize,narvs);     %粒子所在的位置
v=10*rand(particlesize,narvs);         %粒子的飞翔速度

在以上代码参数中，需要重点注意的是惯性因子w，粒子所在位置x，以及粒子的飞翔速度v。当寻优结果陷入局部最优值时，可以调整这三个参数以实现找到全局最优值

其中粒子的最大迭代次数MaxNum可以据适应度函数的复杂度进行增加或减少以优化运行时间。

需要注意的是当适应度函数变为多个自变量时，除了在默认参数的部分对narvs参数值进行修改，在后面的运算代码同样需要进行修正。

如果只是单纯的使用和同纬度数据实例求解，修改以上代码可以达成目标。但是还是有很多情况下有多个自变量，在自变量较少的情况下该算法同样可以达到目标，当自变量个数过多的情况下可以通过结合主成分分析等降维算法进行寻优。

更多应用场景

受时间与篇幅影响，多维的和改进的代码就不在细讲如果想进行更多的交流和沟通，或者了解多个自变量的粒子群算法代码与相关知识，可以关注我建立的公众号“狗头的成长日记”