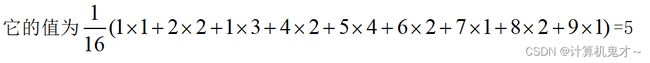数字图像处理（2）

        又到了新的一周，是时候继续学习计算机视觉的先导知识啦！

        上次我们说过，这次的学习路线大致如下图，今天主要是以科普为主，小编会在下一篇文章中讲解实践以及原理。

一、点运算

        点运算：基于点操作，将每一个像素的灰度值按照一定的数学变换公式转换为一个新的灰度值。常用的点运算方法：灰度变换增强、直方图均衡化等方法。

1、灰度变换

        灰度变换：也称为灰度映射，就是将输入图像f(x,y)中的灰度r，通过映射函数T(·)映射成输出图像g(x,y)中的灰度s。

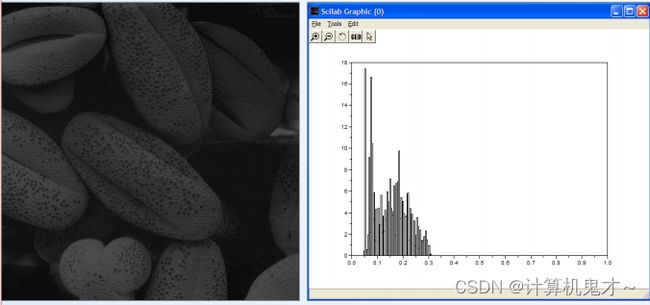
         比如说，女孩子自拍喜欢把自己p图p的白一点，这就是一个很常见的灰度变换。把脸这一部分的灰度值调的高一点。如下图：

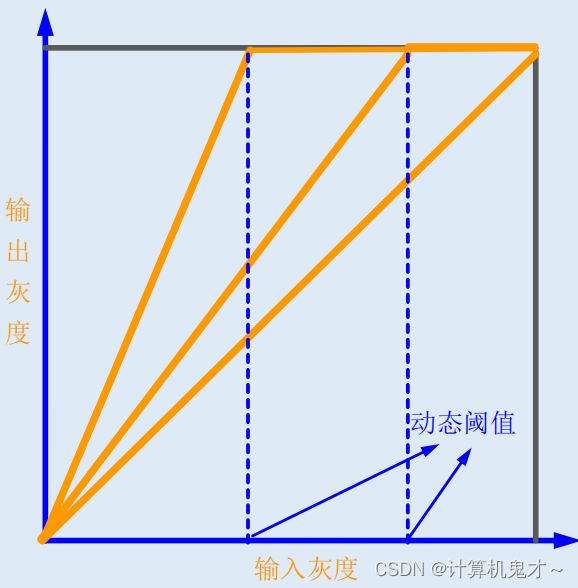
正向45度：恒等变换，输出与输入图像相同

反向45度：反转变换，输出是输入图像的底片效果

图像变亮：正向45度之上，输出灰度比输入灰度更大

图像变暗：正向45度之下，输出灰度比输入灰度更小

斜率大于45度：输出相对于输入图像，灰度值被拉伸

斜率小于45度：输出相对于输入图像，灰度值被压缩

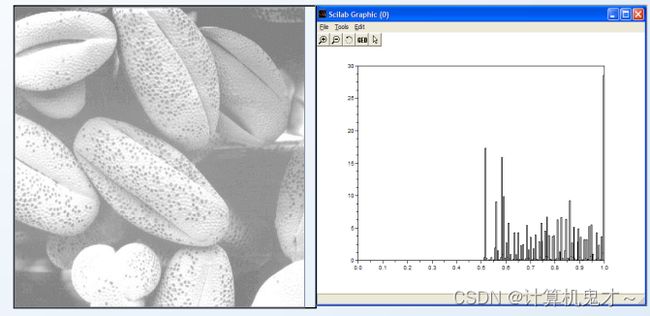
思考题：左边为原图，右边为变换后的图，请仔细观察灰度变换效果，画出变换图（假设该分段变换由两段直线构成）

答案：如下图。由上图知，图像在慢慢变白，黄的变成白的，橙的变成黄色……很明显，每个像素的灰度值都在增加，是吗？错！已经是白色的不会增加到超过255的值，这也是我们解题的关键所在。

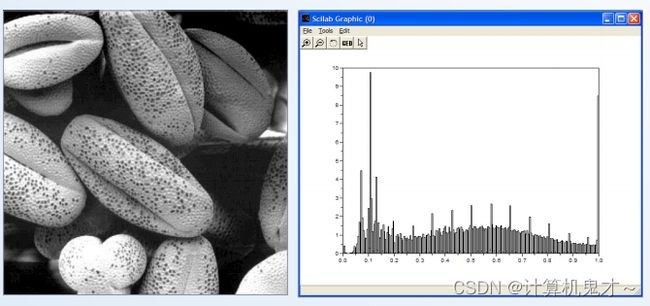
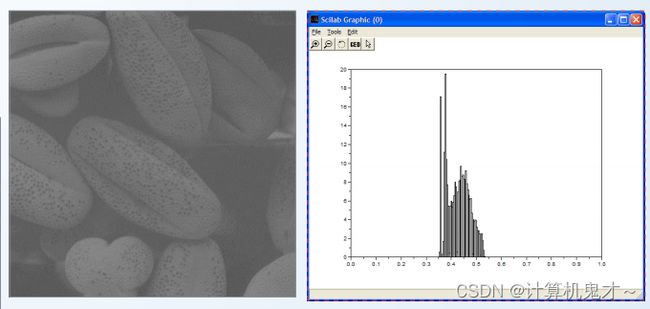
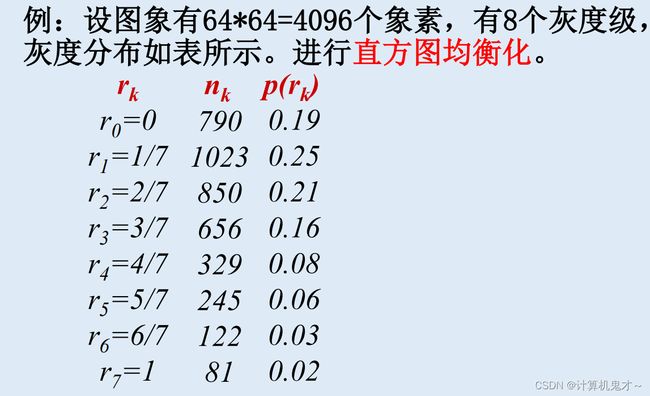
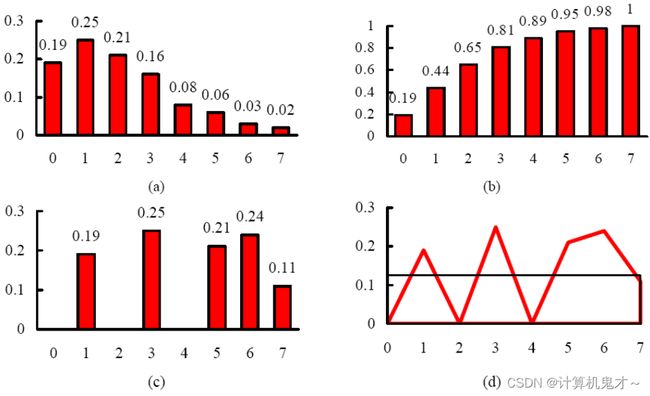
2、直方图增强

        直方图增强：是图像的一种统计表达，它描述了图像中各灰度值的像素个数，反映了该图中

不同灰度级出现的统计概率。

暗图像的直方图分量集中在灰度级的低端

亮图像的直方图分量则倾向于灰度级的高端

高对比度图像的直方图分量覆盖了很宽的灰度级范围

低对比度图像的直方图分量则比较集中

        直方图均衡化的基本思想是把原始图像的直方图变换为均匀分布，以增加像素灰度值的动态范围，从而达到增强图像的目的。

变换函数s=T(r)应满足下列条件原则：

①在0≤r≤1的区间内,T(r)单值单调增加，保证图像的灰度级从黑到白的次序不变

②对于0≤r≤1，有0≤T(r)≤1，保证映射变换后的像素灰度值在允许的范围内

做个题让大家熟悉一下：

        解题思路：先计算累积直方图，再把计算的累积直方图就近安排到8个灰度级中，最后重新命名sk，归并相同灰度级的象素数。

（a）原始直方图     （b）累积直方图     （c）均衡化的直方图    （d）均衡化的像素分布

 二、空间滤波

        空域滤波是一种邻域处理方法，通过直接在图像空间中对邻域内的像素进行处理，达到增强图像的目的。

        从功能和特点两个维度，空域滤波器可分为四类。

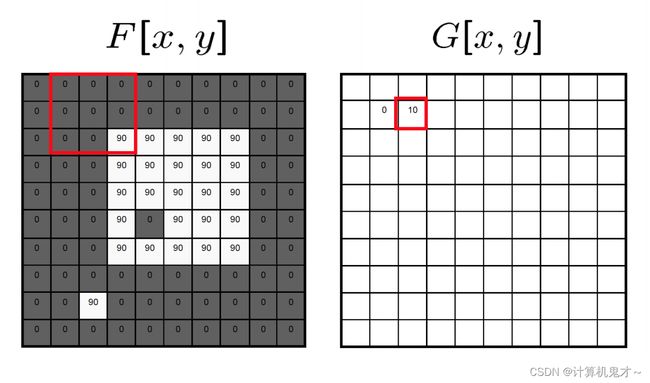
我们先来介绍一个数学概念：互相关，如下图：

 是不是听得云里雾里？好的，那么我们用一个例子来帮助大家理解：

1、平滑

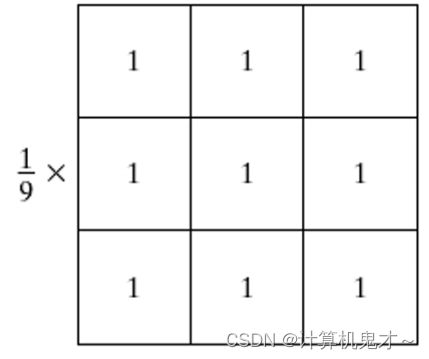
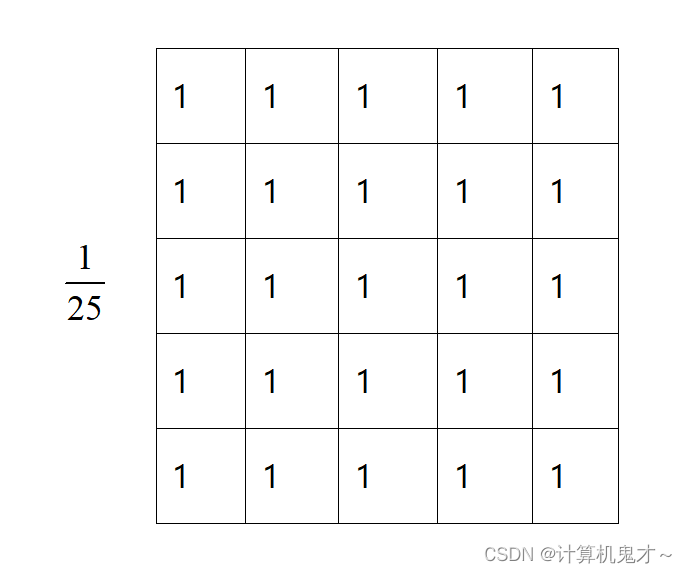
①线性平滑滤波-邻域平均法

        用一个像素的邻域平均值作为滤波结果，此时滤波模板的所有系数都相等，且其和为1。

        

均值滤波3*3的核为：

均值滤波5*5的核为：

以此类推……还有7*7的核、9*9的核，但是核必须为单数 。

以3*3的核为例，执行过程大概如下图：

        邻域平均法的实质是通过一点和邻域内像素点求平均来去除突变的像素点，从而滤掉一定的噪声。其主要优点是算法简单，计算速度快，但其代价是会造成图像一定程度上的模糊。

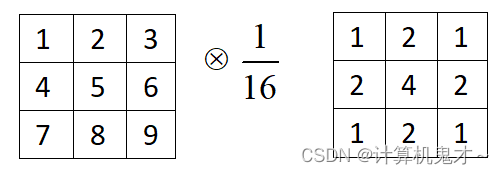
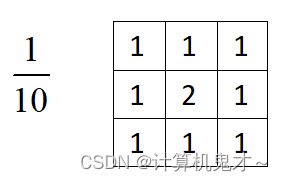
②线性平滑滤波-加权平均法（高斯滤波）

        与邻近平均法的模板不同，中心点或邻域的重要程度也不相同，因此，应根据问题的需要选取合适的模板。但不管什么样的模板，必须保证全部权系数之和为单位值，这样可保证输出图像灰度值在许可范围内， 不会产生“溢出”现象。比如说下面几种核：

2、锐化

        锐化的目的是突出图像中细节或被模糊的细节，锐化可用微分来完成，而微分算术的响应强度与图像在该点的突变程度有关。所以我们使用的是下面这种核，我们称之为拉普拉斯算子：

也就是说，如果该点与周围的点的值差异太大，则锐化后该点会表现出白色。

左边为原图，右边为锐化后的图：

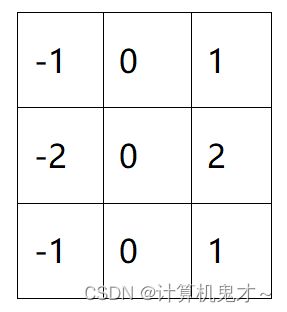
当然了，还有sobel算子如下图，左边是x方向上的锐化，右边是y方向上的锐化

 用左边的核运算，得出来的图像如下图

用右边的核运算得出来的锐化图如下图 

 

 好了，本期的科普就到这里啦，感谢观众老爷们的支持，你们的鼓励是小编写下去最大的支持！