特征工程之PCA降维（主成分分析）总结

1.PCA是什么

PCA是什么？
PCA（Principal Component Analysis）是一种常用的数据分析方法

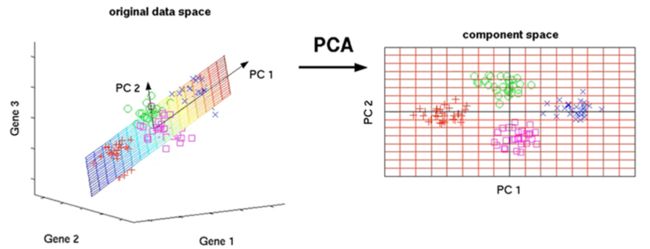
如上图所示，原来是三维的数据，通过分析找出两个主成分 PC1 和 PC2，那么直接在这两个主成分的方向上就可以形成一个平面，这样就可以把我们三位的样本点投射到这一个平面上（如右图）。那么此时的PC1和PC2都不单单是我们的其中某一维特征，而是各个特征通过某种线性变化的组合结果, 这就是PCA降维宏观上的效果。

PCA 通过线性变换将原始数据变换为一组各维度线性无关表示，可用于提取数据的主要特征分量及高维数据的降维, 而转换后的这组变量 PC1、PC2 便是我们所说的主成分。

那PCA降维是如何实现的呢？在讲其具体实现原理前，先要清楚 方差和协方差 的概念：方差大概就是一些点在一个维度的偏差，越分散的话方差越大。而协方差是衡量一个维度是否会对另一个维度有所影响，从而查看这两个维度之间是否有关系。

PCA通过线性变换将元数据映射到新的坐标系中，使映射后的第一个坐标上的方差最大，第一个坐标也就是第一个主成分PC1，以此类推。在sklearn的PCA包中，有一个explained_variance_ratio_，它代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分。

那么，怎么样才能实现“找到那样一个坐标，使得数据在这个坐标上的映射方差最大”呢？按照下面的计算过程就可以实现这个效果。

2. 算法思路

设有 $n$ 条 $d$维数据

详细推算

此部分转自：PCA降维原理 操作步骤与优缺点

首先对于数据集，有m个样本，设每个样本有n个维度。表示如下：

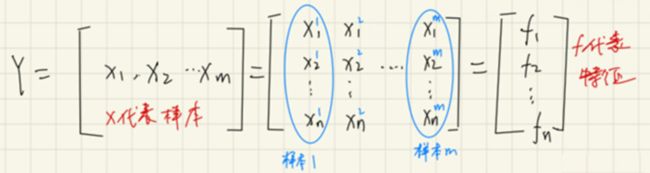
在上图中，其实只要看中间那幅图就行。左图和右图则是分别用来突出样本的和特征的关系，比如第一列，就是第一个样本的所有值；而第一行，就是第一个特征的所有值。

对于每一个维度我们就可以得到均值，如下图所示：

每一个维度减去这个均值，得到一个矩阵（相当于将坐标进行了平移）。

到这里，我们的数据“去中心化”就完成了，这样去中心化的目的就是：让每个特征下的均值都为0，后续计算特征之间协方差的时候就可以简化计算。注意，PCA的降维就是围绕每个特征（即每个坐标轴）进行展开，而不是围绕样本。因为就想开头图上描述的一样，样本点数量是不变化的，但是特征的维度会有改变，导致样本点的形状分布上发生变化。

最终，我们得到的去中心化结果如下:

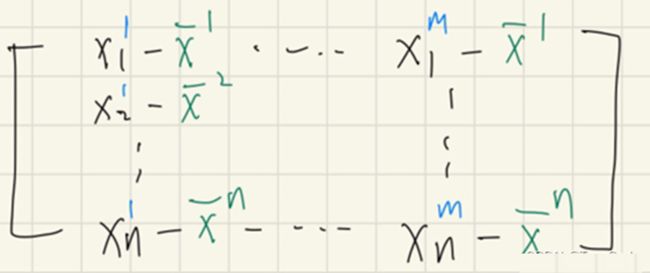
现在，我们需要对处理后的数据在特征维度（也就是各个坐标轴之间）进行协方差矩阵的运算。

在图中我们一共有n个特征，若特征两两组合，我们会得到一个n^2的协方差矩阵（注：a12=a21，即转置值相等）。如下图所示：（其中每个f 就是原数据中一行一行的特征）

而协方差的定义为：

因此，协方差矩阵可以写成：

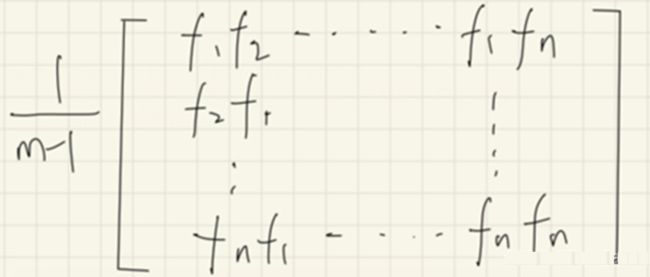
其中，m是样本点的个数，在上面已经提到过了。

（补充一点：其实可以发现，要得到这样的协方差矩阵，只需要原数据乘以自身的转置就能得到，如下图所示：

接下来，就是对协方差矩阵求特征值和特征向量，并根据特征值从大到小排序，每个特征值对应着一个特征向量。对于求特征值和特征向量的方法，其实就是用特征值分解，或者是svd矩阵分解，在这篇文章里有提到过，原理都类似。

矩阵分解是非常常见的操作矩阵方式。尤其是在推荐系统里，我们往往会有一个用户-物品矩阵，这个矩阵非常大，比如100w个用户*1000w个物品矩阵，这个时候我们可以通过矩阵分解一方面降低矩阵的维度，另一方面提取用户和物品各自的信息。

举个例子，对于100w1000w的用户-物品矩阵，我们可以得到100w10的用户矩阵和10*1000w物品矩阵。这样子其中的10维向量就是我们提取的主要特征。一般来说我们会把矩阵先分成三块再得到其中的这两块，具体原因看完这两种分解方式就懂了~

下面没有涉及公式推导，主要是想整理两者的主要区别和记录一下对基本道理的理解。

特征值分解

对于维度为 n*n 并且有 n 个线性无关的特征向量的矩阵 A，按特征值分解，可以分解为：
$$A=U\wedge U^{-1}$$
（下面为了方便打我把中间的符号打成V）

其中 U 是由矩阵的特征向量组成的，V 是由矩阵的特征值组成的对角阵。

这就是特征值分解。

我感觉特征值分解就是帮助我们我们得到矩阵A的特征向量和特征值的。这样子我们就可以在特征向值V中再选取较大的前几个，再提取它们对应的特征向量进一步提取矩阵的主要特征。

但很显然特征值分解的条件很苛刻：需要n*n的方阵，并且要求有n个线性无关的特征向量，所以用的并不多。

优缺点

PCA 本质上是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。

因此，PCA 也存在一些限制，例如它可以很好的解除线性相关，但是对于高阶相关性就没有办法了，对于存在高阶相关性的数据，可以考虑Kernel PCA，通过 Kernel 函数将非线性相关转为线性相关。另外，PCA 假设数据各主特征是分布在正交方向上，如果在非正交方向上存在几个方差较大的方向，PCA 的效果就大打折扣了。

参考链接：

[1] K-means高维聚类与PCA降维 2019.11
[2] PCA 降维算法 —— 原理与实现 2018.6
[3] PCA降维原理 操作步骤与优缺点 2022.5
[4] 高维度数据能否使用kmeans? 2018.8