python-机器学习打卡(五)--监督学习(四)--核支持向量机

核支持向量机

SVM的英文全称是Support Vector Machines，中文叫支持向量机。支持向量机是我们用于分类的一种算法。支持向量也可以用于回归，此时叫支持向量回归（Support Vector Regression,简称SVR）。
SVM的主要思想可以概括为如下两点：
（1）它是针对线性可分的情况进行分析的。对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间，使其线性可分，从而使得在高维特征空间中采用线性算法对样本的非线性特征进行线性分析成为可能。
（2）它基于结构风险最小化理论，在特征空间中构建最优分类面，使得学习器能够得到全局最优化，并且使整个样本空间的期望风险以某个概率满足一定上界。
　　从上面的两点基本思想来看，SVM没有使用传统的推导过程，简化了通常的分类和回归等问题；少数的支持向量确定了SVM 的最终决策函数，计算的复杂性取决于支持向量，而不是整个样本空间，这就可以避免“维数灾难”。少数支持向量决定了最终结果，这不但可以帮助我们抓住关键样本，而且注定了该方法不但算法简单，而且具有较好的“鲁棒”性。
　　
支持向量机SVM、支持向量回归SVR详细推导

线性模型与非线性特性

线性模型在低纬空间中可能非常有限，因为线和平面的灵活非常有限。
先见使用到的数据集进行可视化，该数据集中每个数据点有两个特征，x轴表示特征1，y表示特征二。

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import mglearn
x, y = make_blobs(centers=4, random_state=8)
y = y % 2
mglearn.discrete_scatter(x[:, 0], x[:, 1], y)
plt.show()

预览：（二分类数据集make_blobs，模型不是线性可分的）

使用SVC给出划分后的边界：

from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
import mglearn

x, y = make_blobs(centers=4, random_state=8)
y = y % 2

svc = LinearSVC().fit(x,y)
mglearn.plots.plot_2d_separator(svc,x)

mglearn.discrete_scatter(x[:, 0], x[:, 1], y)
plt.xlabel("Feature 0 ")
plt.ylabel("Feature 1 ")
plt.show()

可以看到用于分类的线性模型在两个特征情况下只能给出一条直线划分，无法给出好的结果。

有一种方法可以使得这种情况的线性模型更加灵活，那就是在添加更多的特征，比如可以将第二个特征的平方作为一个新特征，那么原来数据点就得到了新特征（feature0，feature1，feature1**2）。这样，数据分布就可以画到空间坐标中：

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import mglearn
import numpy as np
from sklearn.svm import LinearSVC
from mpl_toolkits.mplot3d import Axes3D, axes3d

X, y = make_blobs(centers=4, random_state=8)
y = y % 2
X_new = np.hstack([X, X[:, 1:] ** 2])


linear_svm_3d = LinearSVC().fit(X_new, y)
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_

# 首先画出所有y == 0的点， 然后画出所有y == 1的点
mask = y == 0
# 显示线性决策边界
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)

XX, YY = np.meshgrid(xx, yy)  # 生成网格点坐标矩阵
ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3)
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
           cmap=mglearn.cm2, s=60)
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
           cmap=mglearn.cm2, s=60)

ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1 ** 2")
plt.show()

将三维点可视化后，使用SVC给出决策边界，可以看到使用一个平面将数据分类。

核技巧

如果向数据中添加非线性特征，可以使得模型变得强大，但是我们通常并不知道要添加那些特征，添加更多特征可能会导致计算开销大。可以使用核技巧（一种数学技巧，可以在更高维的空间中学习分类器，而不用实际计算可能非常大的数据表示，原理是直接计算扩展特征的表示的数据点之间的距离）来解决这个问题:
将数据映射到高维空间通常有两种办法：

• 多项式核：在一定阶数内计算原始特征所有的可能多项式
• 径向基函数：也叫高斯核。考虑所有阶数的可能的多项式，但阶数越高，特征重要性越低，遵循指数映射的泰勒公式

SVM理解

模型训练过程中，SVM学习每个训练数据点对于两个类别之间的决策边界的重要性。但通常只有一部分数据点对边界来说很重要（位于边界上的点，这些点就叫做支持向量）。

对新样本点进行预测时：需要计算新样本点对于每个支持向量的距离。分类决策是基于他与支持向量之间的距离以及模型训练过程中的支持向量的重要性（保存在SVC的dual＿coef＿属性中）来做出决策的。
数据之间的距离是由高斯核给出的：
$$k_{rbf}(x_1,x_2)=exp(-\gamma ||x_1-x_2|{|}^2)$$
这里的$x_1$和$x_2$是数据点，$||x_1-x_2|{|}^2$ 表示欧式距离 $\gamma$表示高斯核宽度的参数。
下图和代码是对一个二维的二分类数据集使用SVC进行分类的可视化图：
代码1

from sklearn.svm import SVC
import mglearn.datasets
import matplotlib.pyplot as plt

X, y = mglearn.tools.make_handcrafted_dataset()
svm = SVC(kernel='rbf',C = 10,gamma=0.1).fit(X,y)
mglearn.plots.plot_2d_separator(svm,X,eps=.5)#对于二维数据分类任务画出边界
mglearn.discrete_scatter(X[:,0],X[:,1],y)#散点图 参数为二维数据的两个特征点以及数据点的标签

sv = svm.support_vectors_
sc_labels = svm.dual_coef_.ravel()>0

mglearn.discrete_scatter(sv[:,0],sv[:,1],sc_labels,s=15,markeredgewidth=3)
# 参数 s为样本点符号显示的大小，markeredgewidth 表示样本点的边框宽度
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()

预览：

SVM调参

上一个代码中使用了SVM的两个参数 gamma和C

• gamma ： 是高斯核的参数，控制高斯核宽度
• C ：正则化参数，用来限制数据点的重要性
  将代码二添加到代码一中：
  代码二

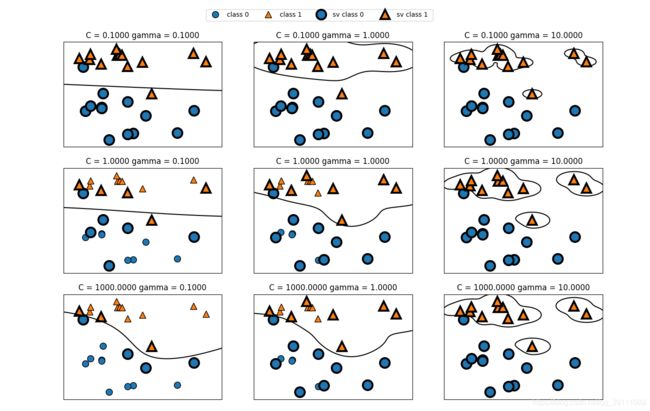
fig ,axes = plt.subplots(3,3,figsize = (15,10))
for ax,C in zip(axes,[-1,0,3]):
    for a,gamma in zip(ax,range(-1,2)):
        mglearn.plots.plot_svm(log_C=C,log_gamma=gamma,ax=a)
axes[0,0].legend(["class 0","class 1" , "sv class 0 ","sv class 1 "],ncol = 4,loc = (.9,1.2))

plt.show()

从左到右gamma值分别设置为0.1，1，10。gamma值较小时，说明高斯核半径大，许多点之间都是可以看做很靠近。使所以左侧的子图边界都很平滑，当gamma值增大时，高斯核半径减小，决策边界更关注单个点，导致模型复杂。

从上到下C的值分别为0.1，1，1000。与线性模型一样，C很小时候说明模型受限，当C的值增大时，模型边界发生弯曲来将点正确分类。

数据预处理

我们可以使用数据预处理对数据点进行缩放，使得每个数据点大致位于同一范围。

from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()
Xtrain, Xtest, ytrain, ytest = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=6)
#找到每个数据点的最小特征值
min_on_training = Xtrain.min(axis=0)
#计算数据点特征的范围值 最大值-最小值
range_on_training = (Xtrain - min_on_training).max(axis=0)
#对训练集和测试集进行缩放，测试集也使用训练集的范围。
pre_train = (Xtrain - min_on_training) / range_on_training
pre_test = (Xtest - min_on_training)/range_on_training
svm = SVC()
svm.fit(Xtrain, ytrain)

print("training set score is {:.3}".format(svm.score(Xtrain,ytrain)))
print("test set score is {:.3}".format(svm.score(Xtest,ytest)))
svm = SVC()
svm.fit(pre_train, ytrain)
print("training set with data preprocessing score is {:.3}".format(svm.score(pre_train,ytrain)))
print("test set with Data preprocessing score is {:.3}".format(svm.score(pre_test,ytest)))

输出

training set score is 0.911
test set score is 0.937
training set with data preprocessing score is 0.981
test set with Data preprocessing score is 0.993

可以看到经过缩放后的模型的性能显著提高，说明数据缩放对模型影响很大。但是模型处于欠拟合状态，我们可以通过修改参数改变模型的复杂度。

小结

优点 ：支持向量机在各种数据上都表现很好。SVM允许决策边界很复杂，即使只有几个数据点，而且无论高维还是低维的特征都有很好的性能。
缺点：调参和数据预处理都需要谨慎。而且模型较难解释。