机器学习6-SVM

1 间隔与支持向量

在训练集样本空间中找到一个划分超平面，使得这个超平面所产生的分类结果是最鲁棒的，对未见示例的泛化能力最强。
$$w^{T}x+b=0$$
w为法向量，决定了超平面的方向，b为位移项8，决定了超平面与原点的距离。
样本空间中任一点x到超平面(w,b)的距离可写为：
$$r=\frac{|w^{T}x+b|}{||w||}$$

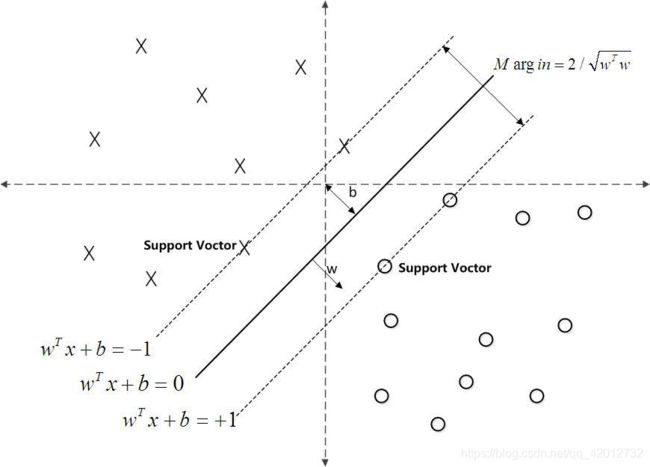
支持向量：距离超平面最近的几个训练样本点
margin：两个异类支持向量到超平面的距离之和：
$$\gamma =\frac{2}{||w||}$$
最大化$\gamma$等价于最小化：
$$mi{n}_{w,b}\frac{1}{2}||w|{|}^2$$
$$s.t.y_i(w^T{x}_i+b)>=1$$
上式是一个凸二次规划问题。
一个高效的解法：用拉格朗日乘子法得到其对偶问题。对约束添加拉格朗日乘子${\alpha }_i>=0$,上式重写为
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))$$
对w，b求偏导为0，可得对偶问题
$$ma{x}_{\alpha }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i>=0$$
通过SMO算法，我们得到了对应的α的值α∗。
那么我们根据$w={\sum }_{i=1}^m{\alpha }_i{y}_i{x}_i$，可以求出对应的w的值.
求出所有支持向量所对应的$b_s^{\ast }$，然后将其平均值作为最后的结果.对于任意支持向量($x_s,y_s$)，都有$y_{s}f(x_s)=1$.

2 线性可分SVM的算法过程

这里我们对线性可分SVM的算法过程做一个总结。

输入是线性可分的m个样本(x1,y1),(x2,y2),…,(xm,ym),其中x为n维特征向量。y为二元输出，值为1，或者-1.

输出是分离超平面的参数$w^{\ast }$和$b^{\ast }$和分类决策函数。

算法过程如下：

1）构造约束优化问题
$$ma{x}_{\alpha }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i>=0$$
2）用SMO算法求出上式最大时对应的α向量的值${\alpha }^{\ast }$向量.
3) 计算$w^{\ast }={\sum }_{i=1}^m{\alpha }_i^{\ast }{y}_i{x}_i$
4) 找出所有的S个支持向量,即满足${\alpha }_s$>0对应的样本$(x_s,y_s)$，通过 $y_s({\sum }_{i=1}^m{\alpha }_i{y}_i{x}_i^T{x}_s+b)=1$，计算出每个支持向量$(x_s,y_s)$对应的$b_s^{\ast }$,计算出这些$b_s^{\ast }=y_s-{\sum }_{i=1}^m{\alpha }_i{y}_i{x}_i^T{x}_s$. 所有的$b_s^{\ast }$对应的平均值即为最终的$b^{\ast }=\frac{1}{S}{\sum }_{i=1}^S{b}_s^{\ast }$
这样最终的分类超平面为：$w^{\ast }x+b^{\ast }=0$，最终的分类决策函数为：$f(x)=sign(w^{\ast }x+b^{\ast })$

3 核函数

如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。假设ϕ是一个从低维的输入空间χ（欧式空间的子集或者离散集合）到高维的希尔伯特空间的H映射。那么如果存在函数K(x,z)，对于任意x,z∈χ，都有：
$$K(x,z)=\varphi (x)\bullet \varphi (z)$$
　　　　那么我们就称K(x,z)为核函数。
K(x,z)的计算是在低维特征空间来计算的，它避免了在高维维度空间计算内积的恐怖计算量。
核函数的条件：一个函数要想成为正定核函数，必须满足他里面任何点的集合形成的Gram矩阵是半正定的。也就是说,对于任意的xi∈χ，i=1,2,3…m, $K(x_i,x_j)$对应的Gram矩阵K=[$K(x_i,x_j)$] 是半正定矩阵，则K(x,z)是正定核函数。　
任何一个核函数都隐式的定义了一个“再生核希尔伯特空间”的特征空间

• 线性核函数：
  $$K(x,z)=x\bullet z$$
• 多项式核函数：
  $$K(x,z)=（\gamma x\bullet z+r{)}^d$$
• 高斯核函数：
  $$K(x,z)=exp(-\frac{||x-z|{|}^2}{2{\sigma }^2})$$
  $\sigma >0$为高斯核的带宽
• 拉普拉斯核函数
  $$K(x,z)=exp(-\frac{||x-z||}{\sigma })$$
  $\sigma >0$
• sigmoid核函数：
  $$K(x,z)=tanh(\beta x^{T}z+\theta )$$

4 软间隔

现实中很难确定适合的核函数使得样本在特征空间线性可分。就算找到某个核函数使训练样本在特征空间线性可分，也很难断定结果是不是过拟合造成的。
办法：允许支持向量机在一些样本数出错。软间隔。
SVM对训练集里面的每个样本(xi,yi)引入了一个松弛变量ξi≥0,使函数间隔加上松弛变量大于等于1，也就是说：
$$y_i(w\bullet x_i+b)\ge 1-{\xi }_i$$
对比硬间隔最大化，可以看到我们对样本到超平面的函数距离的要求放松了，之前是一定要大于等于1，现在只需要加上一个大于等于0的松弛变量能大于等于1就可以了。当然，松弛变量不能白加，这是有成本的，每一个松弛变量ξi, 对应了一个代价ξi，这个就得到了我们的软间隔最大化的SVM学习条件如下：
$$mi{n}_{w,b,{\xi }_i}||w|{|}^2+C\sum _{i=1}^m{\xi }_i$$
$$s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i(i=1,2,...m)$$
$${\xi }_i\ge 0(i=1,2,...m)$$
将软间隔最大化的约束问题用拉格朗日函数转化为无约束问题如下：

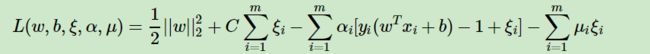
其中 μi≥0,αi≥0,均为拉格朗日系数。
可以先求优化函数对于w,b,ξ的极小值(偏导为0), 接着再求拉格朗日乘子α和 μ的极大值。
$$ma{x}_{\alpha }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,C>={\alpha }_i>=0$$
根据KKT条件中的对偶互补条件${\alpha }_i^{\ast }(y_i(w^T{x}_i+b)-1++{\xi }_i^{\ast })=0$，

5 支持向量回归

支持向量回归假设我们能容忍f(x)与y之间最多有$ϵ$的偏差，超过这个偏差才计算损失。
$$mi{n}_{w,b}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{l}_{ϵ}(f(x_i)-y_i)$$
$$l_{ϵ}(f(x_i)-y_i)=\{\begin{array}{ll}0& |y_i-w\bullet \varphi (x_i)-b|\le ϵ\\ |y_i-w\bullet \varphi (x_i)-b|-ϵ& |y_i-w\bullet \varphi (x_i)-b|>ϵ\end{array}$$

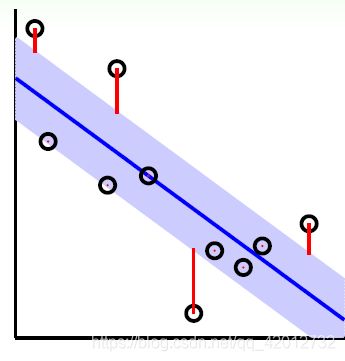
目标函数如下:$$min\frac{1}{2}||w|{|}_2^{2}s.t|y_i-w\bullet \varphi (x_i)-b|\le ϵ(i=1,2,...m)$$
因为间隔带两侧的松弛程度可有所不同，定义两个松弛变量${\xi }_i^{\vee },{\xi }_i^{\wedge }$
$$min\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m({\xi }_i^{\vee }+{\xi }_i^{\wedge })$$
$$s.t.-ϵ-{\xi }_i^{\vee }\le y_i-w\bullet \varphi (x_i)-b\le ϵ+{\xi }_i^{\wedge }$$
$${\xi }_i^{\vee }\ge 0,{\xi }_i^{\wedge }\ge 0(i=1,2,...,m)$$
用拉格朗日函数将目标优化函数变成无约束的形式:
$$L(w,b,{\alpha }^{\vee },{\alpha }^{\wedge },{\xi }_i^{\vee },{\xi }_i^{\wedge },{\mu }^{\vee },{\mu }^{\wedge })=\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m({\xi }_i^{\vee }+{\xi }_i^{\wedge })+\sum _{i=1}^m{\alpha }^{\vee }(-ϵ-{\xi }_i^{\vee }-y_i+w\bullet \varphi (x_i)+b)+\sum _{i=1}^m{\alpha }^{\wedge }(y_i-w\bullet \varphi (x_i)-b-ϵ-{\xi }_i^{\wedge })-\sum _{i=1}^m{\mu }^{\vee }{\xi }_i^{\vee }-\sum _{i=1}^m{\mu }^{\wedge }{\xi }_i^{\wedge }$$
目标是：
$$\underset{w,b,{\xi }_i^{\vee },{\xi }_i^{\wedge }}{min}\underset{{\mu }^{\vee }\ge 0,{\mu }^{\wedge }\ge 0,{\alpha }_i^{\vee }\ge 0,{\alpha }_i^{\wedge }\ge 0}{max}L(w,b,{\alpha }^{\vee },{\alpha }^{\wedge },{\xi }_i^{\vee },{\xi }_i^{\wedge },{\mu }^{\vee },{\mu }^{\wedge })$$
以先求优化函数对于$w,b,{\xi }_i^{\vee },{\xi }_i^{\wedge }$的极小值, 接着再求拉格朗日乘子${\alpha }^{\vee },{\alpha }^{\wedge },{\mu }^{\vee },{\mu }^{\wedge }$的极大值。
$$\frac{\partial L}{\partial w}=0\Rightarrow w=\sum _{i=1}^m({\alpha }_i^{\wedge }-{\alpha }_i^{\vee })\varphi (x_i)$$
$$\frac{\partial L}{\partial b}=0\Rightarrow \sum _{i=1}^m({\alpha }_i^{\wedge }-{\alpha }_i^{\vee })=0$$
$$\frac{\partial L}{\partial {\xi }_i^{\vee }}=0\Rightarrow C-{\alpha }^{\vee }-{\mu }^{\vee }=0$$
$$\frac{\partial L}{\partial {\xi }_i^{\wedge }}=0\Rightarrow C-{\alpha }^{\wedge }-{\mu }^{\wedge }=0$$
最终得到的对偶形式为：
$$\underset{{\alpha }^{\vee },{\alpha }^{\wedge }}{max}-\sum _{i=1}^m(ϵ-y_i){\alpha }_i^{\wedge }+(ϵ+y_i){\alpha }_i^{\vee })-\frac{1}{2}\sum _{i=1,j=1}^m({\alpha }_i^{\wedge }-{\alpha }_i^{\vee })({\alpha }_j^{\wedge }-{\alpha }_j^{\vee })K_{ij}$$
$$s.t.\sum _{i=1}^m({\alpha }_i^{\wedge }-{\alpha }_i^{\vee })=0$$
$$0<{\alpha }_i^{\vee }<C(i=1,2,...m)$$
$$0<{\alpha }_i^{\wedge }<C(i=1,2,...m)$$

6 SVM优缺点

SVM算法的主要优点有：

1) 解决高维特征的分类问题和回归问题很有效,在特征维度大于样本数时依然有很好的效果。

2) 仅仅使用一部分支持向量来做超平面的决策，无需依赖全部数据。使得该算法简单且具有较好的“鲁棒”性。

3) 有大量的核函数可以使用，从而可以很灵活的来解决各种非线性的分类回归问题。

4)样本量不是海量数据的时候，分类准确率高，泛化能力强。
5）类别不平衡影响不大

SVM算法的主要缺点有：

1) 如果特征维度远远大于样本数，则SVM表现一般。

2) SVM在样本量非常大，核函数映射维度非常高时，计算量过大，不太适合使用。

3）非线性问题的核函数的选择没有通用标准，难以选择一个合适的核函数。

4）SVM对缺失数据敏感。

7 面试问题收集

如何定义这条曲线最佳？
Hinge(合页)损失最小

为什么需要间隔最大化？
（1）SVM算法认为靠近决策边界的点与决策边界的距离最大时，是最好的分类选择
（2） 因为“正中间”的划分超平面对训练样本局部扰动的“容忍性”好，分隔超平面所产生的分类结果是最鲁棒的，对预测样本泛化能力最强；
（3）线性条件下，分类超平面的解唯一

svm的对偶原理?
把目标函数和约束全部融入一个新的函数，即拉格朗日函数，原始问题就变成了一个极大极小问题，min(w,b)->max(乘子a)，再通过这个函数来寻找最优点。

为什么要使用对偶?
（1） 数学层面上，求解更容易；
（2）分类性能上，自然引入核函数，可推广到非线性问题上。

为什么引入核函数?
线性不可分时，可将样本从原始空间映射到一个更高维的特征空间，使得线性可分。

SVM常见的核函数？
线性、多项式、高斯（灵活，易过拟合，需要样本量大）、sigmod

什么SVM对缺失特征数据敏感？
因为SVM涉及距离度量，缺失数据若处理不好可能会导致分类效果差。SVM没有处理缺失值的策略（而决策树，XGBOOST有）。

SVM是用的是哪个库？
sklearn实现的。采用sklearn.svm.SVC设置的参数, sklearn.svm.SVC(C=1.0, kernel=‘rbf’, degree=3, gamma=‘auto’, coef0=0.0, ……)

SVM参数？
最重要的参数有2个：惩罚系数C与$\gamma (=1/\sigma 2)$，CCC类似于正则化中1/λ的作用。C越大，说明越不能容忍出现误差，越容易过拟合。σ越大，核函数越平滑，波动越小，对噪声越不敏感，易欠拟合；σ越小，高斯分布长得又高又瘦， 会造成只会作用于支持向量样本附近，对于未知样本分类效果很差。

SVM如何实现多分类？
(1) 训练k个分类器，训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类，最后分类时，将未知样本分类为具有最大分类函数值的那类；
(2) 训练c(2,k)个分类器取多数

SVM降低模型复杂度（过拟合）的方法？
给每个样本引入松弛变量

SVM做回归SVR?
一串连续数值向量A=（x1,x2,x3,…xi）对应其函数值(y1,y2,y3…yi)，将其翻转后成为一列数据，类似SVM的不同样本，剩余步骤和SVM类似。只是SVR希望大部分点在间隔内，间隔外的点会带来损失，而SVM希望大部分点在间隔两边。

函数间隔和几何间隔区别？
函数间隔主要表示是否分类正确，可正可负；几何间隔表示点到超平面的距离，只能为正。

SVM与树模型间的区别？
(1)SVM可解释性更弱；树模型可解释性好
(2)SVM对缺失特征数据敏感；树模型对缺失特征数据不敏感
(3)SVM处理多分类问题麻烦
(4)SVM对异常值不敏感；树模型对异常值敏感
(5)SVM泛化能力强；树模型依赖训练样本集，对没有出现的特征没有办法
(6)SVM适用于处理小样本训练集；树模型可处理大样本训练数据集

LR与SVM的区别：
（1）异常值：LR的目标是使得所有的点分类正确。所以LR会受到数据集中所有点的影响，当数据不均衡时，LR的性能会受到影响；而SVM分类性能只会受到支持向量的影响，只要支持向量不变，类别不平衡影响不大；也就是，LR对异常值敏感。
（2）起作用点的范围：LR模型尽量让所有点都远离超平面，而SVM让只考虑support vectors(最难划分/最靠近中间分割线的那些点)，也就是和分类最相关的少数点，尽量远离超超平面，即只用到那些支持向量的样本。也就是SVM的约束来体现的
（3）loss:目标函数不一样,LR对数似然损失函数，SVM凸优化问题。
（4）非线性：处理非线性分类时，SVM采用核函数更好更快，LR很少使用核函数
（5）Linear SVM依赖数据表达的距离测度，所以需要对数据先做normalization；LR不受其影响，但是如果要正则的话也要归一化
（6）概率值：SVM不能给出概率结果，LR可以产生概率，因此可做ranking
（7）SVM的目标函数就自带有约束正则（目标函数中的$\frac{1}{2}||w|{|}^2$项），这就是为什么SVM是泛化力更强的原因。而LR必须另外在损失函数上添加正则项。
（8）LR可解释性更强

SVM与感知机的区别
（1）解：SVM基于间隔最大化，求得分类超平面，解是唯一，且分类结果最鲁棒，泛化能力强；感知机基于误分类最小策略，求得分离超平面，不唯一
（2）学习策略：感知机使用梯度下降；SVM使用由约束条件构造拉格朗日函数，然后求偏导令其为0求得极值点。

转载自：https://blog.csdn.net/UniqueenCT/article/details/88914657

8 SMO算法求解对偶问题

https://www.cnblogs.com/jerrylead/archive/2011/03/18/1988419.html
https://www.cnblogs.com/pinard/p/6111471.html