机器学习实战—无监督学习之聚类

一.无监督学习简介

在前面的学习中，机器学习的应用都是基于有监督学习的，即处理的数据都是有标签的（例如鸢尾花数据集的标签就是鸢尾花的类别），然而绝大多数可用数据都是没有标签的，我们输入特征X，但是没有标签y。在前面我们已经讲过了最常见的无标签学习任务：降维，下面将学习一些其它的无监督学习任务和算法。

二.聚类

2.1 简介

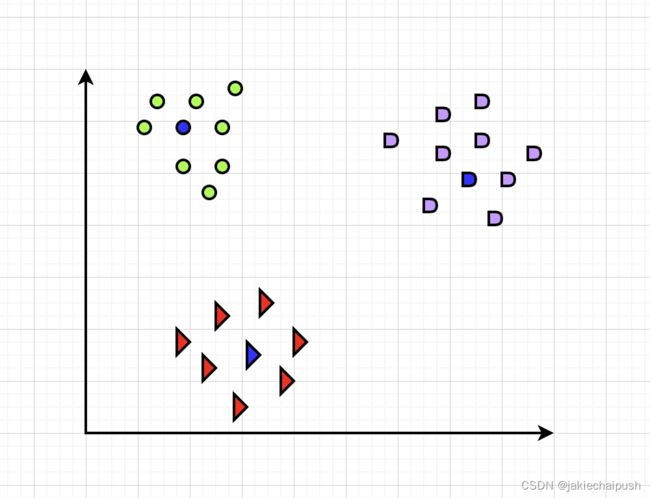
所谓的聚类就是识别相似的实例并将其分配给相似实例的集群或组。就像在分类中一样，每个实例都会分配一个组，但不同的是聚类在分类之前是不知道实例有多少类别的（即数据是没有标签的），我们也无从得知聚类算法会把我们的实例分成几个组别（实际在算法中我们是可以手动指定的）。聚类可应用于各种应用程序，包括：客户细分、数据分析、降维技术、异常检测、半监督学习、搜索引擎和分割图像等。

2.2 聚类算法K-Means

2.2.1 简介

K-means是由贝尔实验室的Stuart Lloyd在1957年提出来的，最开始是用于脉冲编码调制，直到1982年才将该算法对外公布。1965年，Edward W.Forgy发布了相同的算法，因此K-Means有时被称为Lloyd-Forgy

2.2.2 K-means原理

k-means的原理很简单,首先在数据当中随机生成k个聚类中心,然后计算数据当中每个样本到这k个聚类中心的距离,并将对应的样本分到距离最小的聚类中心所对应的簇当中,将所有样本归类之后,对于每一个k个簇重新计算每个簇的聚类中心,也就是每个簇中的所有样本的质心,重复上述操作,直到聚类中心不发生改变为止，例如下图K-means使用的过程为：
（1） K-means算法首先需要选择3个初始化聚类中心
（2） 计算每个数据对象到K个初始化聚类中心的距离，将数据对象分到距离聚类中心最近的那个数据集中，当所有数据对象都划分以后，就形成了3个数据集（即3个簇）
（3）接下来重新计算每个簇的数据对象的均值，将均值作为新的聚类中心
（4）最后计算每个数据对象到新的3个初始化聚类中心的距离，重新划分
（5）每次划分以后，都需要重新计算初始化聚类中心，一直重复这个过程，直到每个簇的聚类中心都不发生变化

2.2.3 K-means使用

1. 导入数据集

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

Data=pd.read_csv("Mall_Customers.csv")
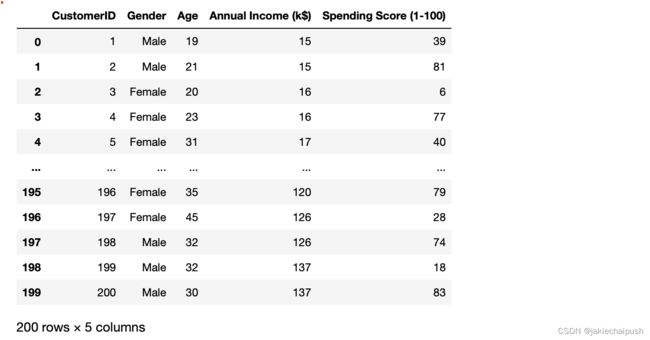
Data

数据集简介：该数据集包含5列，分别为顾客ID（用来唯一标识每一类顾客），性别，年龄，年收入和商场根据顾客行为和消费性质分配的分数。数据集下载地址：点我

2. 使用Seaborn可视化数据集分布

import seaborn as sns
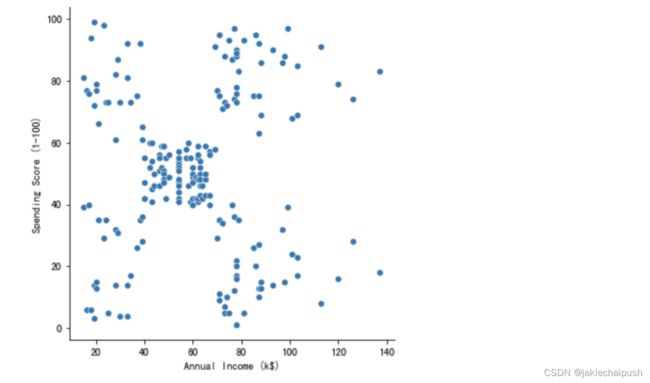
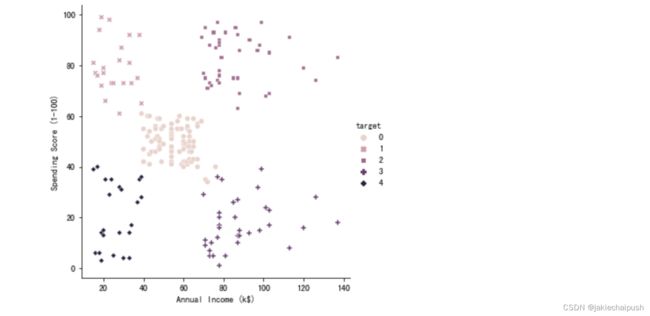
sns.relplot(x="Annual Income (k$)", y="Spending Score (1-100)", data=Data)

从上面的散点图可以看出数据大概分为5个簇

3. 给数据集训练一个K-Means聚类器

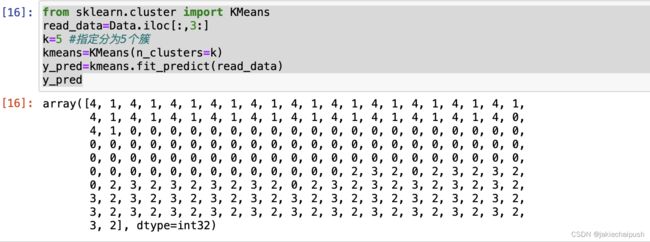
from sklearn.cluster import KMeans
read_data=Data.iloc[:,3:]
k=5 #指定分为5个簇
kmeans=KMeans(n_clusters=k)
y_pred=kmeans.fit_predict(read_data)
y_pred

聚类结果如下：可以看出聚成了5类

4. 查看聚类效果

Data["target"]=y_pred
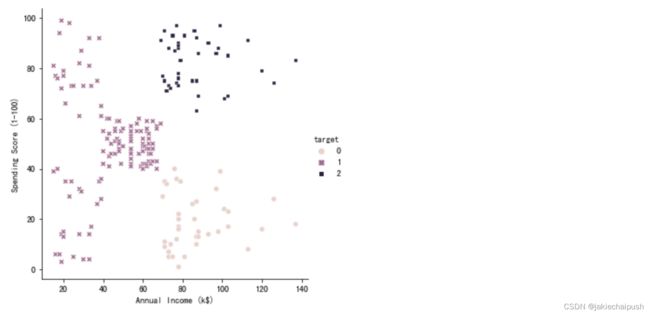
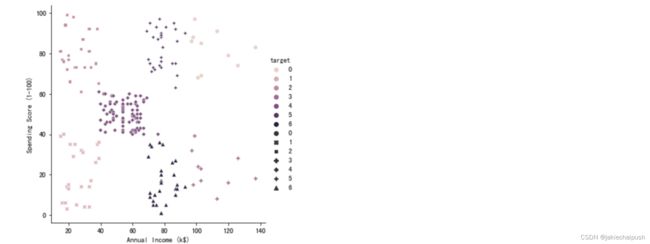
sns.relplot(x="Annual Income (k$)", y="Spending Score (1-100)",hue="target" ,style="target",data=Data)

可以发现聚类效果还是非常理想的

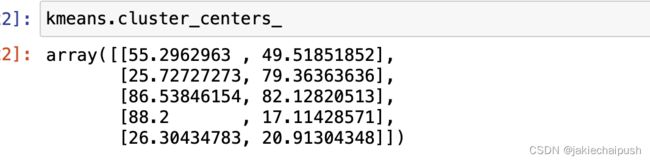
5. 查看聚类中心点

kmeans.cluster_centers_

2.2.4 中心点初始化方法

我们知道对于K-means算法来说，最重要是找到合适的聚类中心，如果能够一次找到合适的聚类中心能够大大减少算法迭代的次数，提高算法的效率，那么如何去初始化中心点，考虑两个场景：

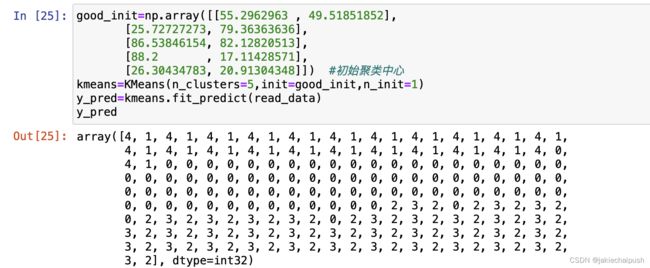
1. 假如我们已经提前知道了聚类中心点的所在位置，例如上面案例我通过kmeans.cluster_centers_获取了最终中心点的位置，假如我们已经提前知道了这个数组集合，我们就可以在K-means初始化时直接将其设置为初始聚类中心，，使用方法如下：

good_init=np.array([[55.2962963 , 49.51851852],
       [25.72727273, 79.36363636],
       [86.53846154, 82.12820513],
       [88.2       , 17.11428571],
       [26.30434783, 20.91304348]])  #初始聚类中心
kmeans=KMeans(n_clusters=5,init=good_init,n_init=1)
y_pred=kmeans.fit_predict(read_data)
y_pred

init：设置中心点列表（Numpy数组）
n_init=1：随机初始化时使用

2. 另一种情况就是，我不知道中心聚类点的位置，但是我可以使用的随机初始化多次运行方法，随机初始化数量由超参数n_init控制，默认情况下，它等于10，所以调用fit()时，随机初始化算法会被运行10次，然后Scikit-learn会将最优的一次替我们保留下来。如何评断这个最优？在这里scikit-learn使用的是性能指标，这个指标称为模型的惯性，即每个实例与其最接近中心点之间的均方距离（均方距离越大模型越差）

可以通过inertia_来获得模型的惯性

2.2.4 K-means++

David Arthur和Sergei Vassilvitskii在选取初始化聚类中心时，对K-means算法提出来改进，而这个改进后的版本就是K-means++，这是一个更加智能的初始化步骤，该步骤倾向于选择彼此相距较远的中心点，这一改进使得K-means算法收敛得到次优解的可能性很小，但会引入额外的计算量。其工作原理如下：

1. 选取一个中心点$c_1$，从数据集中随机选择一个中心点
2. 取一个新中心点$c_i$，选择一个概率为$\frac{D(x^i)}{{\sum }_{j=1}^{m}D(x_j{)}^2}$的实例$x_i$，其中$D(x_i)$是实例$x_i$与已经选择的最远中心点的距离，这样就确保了选择距离已选择的中心点最远的实例会被选作中心点
3. 重复上面步骤，直到选择了所有k个中心点，这样初始化中心点工作就完成了

k-means在默认情况下会选择Kmeans++，如果我们要使用原始的K-means初始化算法，就将超参数init设置为random即可

2.2.5 加速的K-means和小批量K-means

加速的k-means是Charles Elkan在2003年的一篇论文中提出的对原始K-means算法的一个改进，该改进后的算法通过避免许多不必要的距离计算，大大加快了算法的速度。ELkan通过利用三角不等式来加速K-meas，这里引用一篇论文来解释其加速原理。加速的K-means是Kmeans类默认使用的算法。

小批量K-Means是David Sculley在2010年的一篇论文中提出的K-Means算法的另一个重要变体。该算法能够在每次迭代中使用小批量K-means稍微移动中心点，而不是咋每次迭代中使用完整的数据集。这将算法的速度提高了3到4倍，并且可以对不容纳内存的大数据集进行聚类。Scikit-Learn在MiniBatchKMeans中实现了此算法。

from sklearn.cluster import MiniBatchKMeans
minibatch_lmeans=MiniBatchKMeans(n_clusters=5)
minibatch_lmeans.fit(read_data)

2.2.6 寻找最佳聚类数

前面介绍了如何初始化中心聚点的问题，在使用K-means算法的另一个问题就是如何去定簇数（即算法中的k值），像上面的案例中我们可以一眼就可以看出有5个簇，但在实际问题中有时候不是那么容易通过肉眼观察出簇的数量，如果错误的设置簇数会导致一些错误的情况如下：

簇数量设置过少：单独的集群会合并

簇数量设置过多：某些集群会被划分为多个

所以如和正确的确定聚类的簇数，这里有两个思路：

通过惯性曲线来判断：

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()  # 声明使用 Seaborn 样式
tmplist = []
a=[2,3,4,5,6,7,8]
i = 1
for i in a:
    kmeans=KMeans(n_clusters=i)
    kmeans.fit_predict(read_data)
    tmplist.append(kmeans.inertia_)
plt.xlabel("cu")
plt.ylabel("guanxing")
plt.plot(a, tmplist, '-o', color='y',)

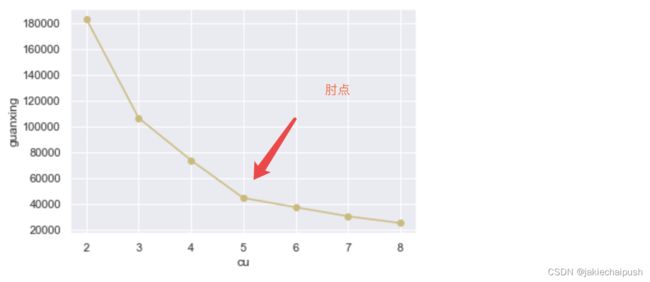
可以看见在惯性系数和簇的关系图中，在簇数为5的地方明显有一个拐点，通常把拐点处的簇数设置为模型的簇数可以取得较好的效果，但这种方法非常的粗糙。

通过轮廓分数判断

这是一种较为精确的方法，所谓轮廓分数就是所有实例的平均轮廓系数，某个实例的轮廓系数的计算方法如下：
$$\frac{(b-a)}{max(a,b)}$$
其中a是与同一集群中该实例与其他实例的平均距离，b是平均最近集群距离（即该实例到最近的集群（不是该实例所在的集群）里面所有实例距离的平均距离），从公式看出轮廓系数只能在-1和+1之间发生变化，轮廓系数越接近+1表示该实例很好地位于其自身的集群中，并且远离其它集群，而接近0表示该实例接近当前两个集群的边界（当前集群和最近的集群），最后轮廓系数接近-1表示该实例可能分配给了错误的集群。轮廓分数就是该集群内所有实例的平均轮廓系数，在Scikit-learn中计算轮廓分数的方法如下：

from sklearn.metrics import silhouette_score
silhouette_score(read_data,kmeans.labels_)

下面看一下簇数与轮廓系数之间的关系：

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()  # 声明使用 Seaborn 样式
tmplist = []
a=[2,3,4,5,6,7,8]
i = 1
for i in a:
    kmeans=KMeans(n_clusters=i)
    kmeans.fit_predict(read_data)
    tmplist.append(silhouette_score(read_data,kmeans.labels_))
plt.xlabel("cu")
plt.ylabel("guanxing")
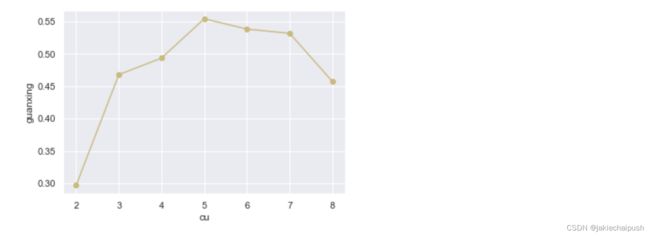
plt.plot(a, tmplist, '-o', color='y',)

可以发现5的轮廓分数是最高的，也就是5是最好的簇数，这就是通过轮廓分数来判断最佳簇数的原理

二.聚类的应用-使用聚类进行图像颜色分割

图像分割是将图像分成多个分割的任务。在语义分割中，属于同一对象类型的所有像素均被分配给同一分割。例如，在无人驾驶汽车的视觉系统中，可能会将行人图像中的所有像素都分配给行人（会有一个包含所有行人的分割），现在使用卷积神经网络的复杂结构可以实现语义分割或实例分割。这里我们利用聚类来做一些简单的事—实现图像的颜色分割。

1. 源图片这里我找了一个简单的花朵的图片，如下

2. 首先使用Matplotlib的imread()函数加载图像

from matplotlib.image import imread
import os
image=imread(os.path.join("/Users/jackchai/Desktop/Python深度学习+机器学习/运行程序/flower.jpg"))
image.shape

图像表示为3D数组。第一维的大小是高度，第二个是宽度，第三个是颜色通道的数量，在这种情况下为三原色（RGB）。换句话说，每个像素都有一个3D向量，包括红色、绿色和蓝色的强度。

3. 使用K-means将这些颜色聚类

X=image.reshape(-1,3)
kmeans=KMeans(n_clusters=10).fit(X)
segmented_img=kmeans.cluster_centers_[kmeans.labels_]
segmented_img=segmented_img.reshape(image.shape)
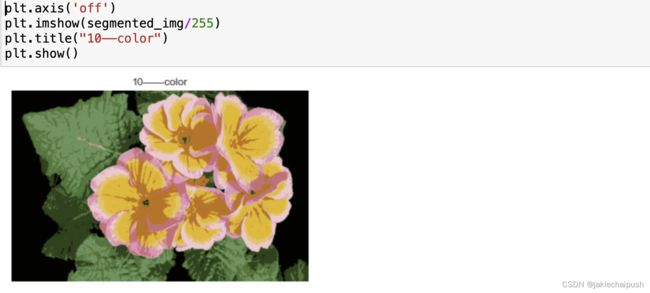
plt.axis('off')
plt.imshow(segmented_img/255)
plt.title("10——color")
plt.show()

聚为两10类说明最后图片会被处理为10种颜色

如果我们设置为2个聚类，最后图片也只会有两个颜色

上面过程会识别某个颜色的颜色聚类。解下来，对于每种颜色，它都会寻找像素颜色集群的平均颜色，然后所有该类的颜色都会由这个平均颜色替换，所有聚类越多，图片颜色辨识度就会越高。当然聚类除了可以应用于图像处理还可以利用到很多领域，这里就不一一介绍了。