机器学习经典算法-人工神经网络之反向传播算法

机器学习经典算法-人工神经网络之反向传播算法

简介

人工神经网络的研究在一定程度上受到了生物学的启发，因为生物的学习系统是由相互连接的神经元组成的异常复杂的网络。而人工神经网络与此大体相似，它是由一系列简单单元相互密集连接构成，其中每一个单元有一定数量的实值输入，并产生单一的实数值输出。（机器学习 Tom M. Mitchell）

神经网络学习方法对于逼近实数值、离散值或向量值的目标函数提供了一种鲁棒性很强的方法，本文要描述的反向传播算法已经在很多实际问题中取得了惊人的成功，本文最终实现的学习器可以以较高的正确率识别手写的单个数字。

实际上，本文并未打算对数学原理做过多的推导，而是以一个初学者的眼光对自己的理解做一个简单的介绍。如果读者是初学者，那么本文应该会给你一些帮助；如果你已经有了一定的理解，那么本文可能不是你想要的内容。

适合神经网络学习的问题：

实例是用很多“属性-值”对表示的
训练数据可能包含错误
可以长时间训练
可能需要快速求出目标输出

简单的学习模型：感知器

感知器以一个实数向量 x⃗ =[x1,x2,…,xn]T 作为输入，通过权值向量 w⃗ =[w0,w1,…,wn] 计算这些输入的线性组合，如果结果大于某个阈值就输出1，否则输出-1。

o(x1,…,xn)={1−1ifw0+w1x1+w2x2+⋯+wnxn>0otherwise

为了方便描述，常常附加一个常量 x0=1 ，上述函数就可以写成：

o(x⃗ )=sgn(w⃗ ⋅x⃗ )

其中

sgn(y)={1−1ify>0otherwise

那么一个感知器表示什么含义呢？想象一下

f(x⃗ )=w⃗ ⋅x⃗ =w0+w1x1+w2x2+⋯+wnxn

如果读者有解析几何的基础，会发现这个函数在一个n维超空间中描述了一个超平面。举一个简单的例子： f(x)=k⋅x+b 在二维空间中表示一条直线，这条直线将空间分成两部分 f(x)>0 和 f(x)<0 。

感知器可以用来表示布尔函数，如果用1（真）和-1（假）表示布尔值，那么一个两输入的感知器可以实现“与”、“或”、“与非”、“或非”，想一想，要想得到正确的输出，权值向量应该如何设置？

一般来说，我们并不知道每个输入的权值（不然这个算法就没有意义了），为了得到近似正确的权值，一般先将权值设置为随机的数，然后使用训练样例进行训练，只要感知器输出错误，就根据正确的输出对权值进行调整。

wi←wi+Δwi

其中

Δwi=η(t−o)xi

t 表示正确的输出，o表示感知器的输出， η 表示学习速率，通常设为较小的数值（例如0.1）。

可微阈值单元

由以上的知识可以知道，单个感知器只能表示线性的决策面，而反向传播算法需要能够表示非线性的曲面。一种方案是sigmoid单元，它和感知器非常类似，不过它的输出不是阶梯型函数，而是平滑的可微阈值函数。

sigmoid单元这样计算输出：

o=σ(w⃗ ⋅x⃗ )

其中

σ(y)=11+e−y

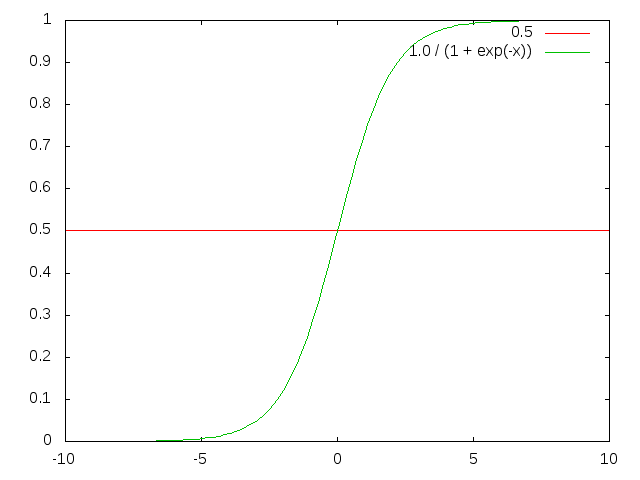
σ 函数的值域为(0, 1)，由于函数把非常大的范围映射到小范围的输出，经常称为sigmoid单元的挤压函数。它的导数

dσ(y)dy=σ(y)⋅(1−σ(y))

可以用它的输出来表示，对反向传播算法来说，这是一个非常有用的特征。也可以采用具有同样特征的其他函数来代替，比如双曲正切函数 tanh 。

反向传播算法

单个学习单元表示的内容是有限的，我们需要一个由一系列单元组成的多层网络，反向传播算法可以用来根据训练结果更新这个网络的权值，直到达到预定的目标（较低的误差或较高的正确率）。误差的定义为

E(w⃗ )=12∑d∈D∑k∈outputs(tkd−okd)2

其中outputs是网络单元的输出集合，D是训练样例集合， tkd 和 okd 是训练样例d的第k个输出单元相关的输出值。下图为一个多层网络：

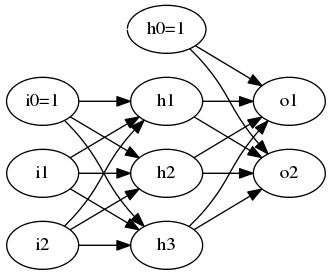
反向传播算法描述

Backpropagation(examples, η , ni , no , nh )
examples中每个样例是输入 x⃗  和目标输出 t⃗  的有序数对
η 是学习速率， ni 是输入数量， no 是输出单元数， nh 是隐藏层单元数
单元i到单元j的输入为 xji ，单元i到单元j的权值为 wij

根据每层单元的数量创建网络，并随机初始化权值
在遇到终止条件前，执行
对于examples中的每个 <x⃗ ,t⃗ >
把 x⃗  输入网络，得到输出o
对于每个输出单元k，计算误差项
δk←ok(1−ok)(tk−ok)
对于每个隐藏单元，计算误差项
δh←oh(1−oh)∑k∈outputswkhδk
更新每个网络权值
wji←wji+Δwji
Δwji=ηδjxji

反向传播算法采用了梯度下降法使误差值更快地下降，但该方法的证明设计较多的数学知识，作者不能保证自己已经理解，故略去。

算法实现简述

此处实现了一个包含一个隐藏层的网络，实际上，大部分情况下一个隐藏层已经足够了，有时为了得到更好的结果会采用多个隐藏层，但基本思想是不变的。一个反向传播算法的类包含了以下属性：

class BPNN
{
    typedef std::vector<double> vd;
    typedef std::vector     vvd;
private:
    int    num_in;            // 输入层向量维度
    int    num_hid;           // 中间层向量维度
    int    num_out;           // 输出层向量维度
    vd     vec_in;            // 输入层向量
    vd     vec_hid;           // 中间层向量
    vd     vec_out;           // 输出层向量
    vd     delta_out;         // 输出层误差
    vd     delta_hid;         // 中间层误差
    vd     const_in;          // 常数项权值
    vd     const_hid;         //
    vvd    in_hid;            // 输入层到中间层的权值
    vvd    pre_in_hid;        // 上一次的调整量
    vvd    hid_out;           // 中间层到输出层的权值
    vvd    pre_hid_out;
    double learn_rate;        // 学习速率
    double momentum;          // 冲量项
    bool   initialized;       // 参数是否初始化
};

通过输入计算输出的方法如下：

/*
 * function: BPNN::compute 根据输入向量计算输出向量
 * _in: 输入向量
 * return: 输出层向量的引用
 * 
 */
const BPNN::vd& BPNN::compute(const vd& _in)
{
    if(!initialized) exit(1); // 未初始化
    assert((int)_in.size() >= num_in);
    std::copy_n(_in.begin(), num_in, vec_in.begin());
    std::fill(vec_hid.begin(), vec_hid.end(), 0.0);
    std::fill(vec_out.begin(), vec_out.end(), 0.0);
    // 权值矩阵乘以输入向量得到输出向量
    for(int i = 0; i < num_hid; ++i)
        for(int j = 0; j < num_in; ++j)
            vec_hid[i] += in_hid[i][j] * vec_in[j];
    for(int i = 0; i < num_hid; ++i)
        vec_hid[i] = sigmoid(vec_hid[i] + const_in[i]);

    for(int i = 0; i < num_out; ++i)
        for(int j = 0; j < num_hid; ++j)
            vec_out[i] += hid_out[i][j] * vec_hid[j];
    for(int i = 0; i < num_out; ++i)
        vec_out[i] = sigmoid(vec_out[i] + const_hid[i]);
    return vec_out;
}

误差反向传播的方法如下：

/*
 * function: BPNN::learn 根据输入和目标输出进行学习
 * _in: 输入向量
 * out: 目标输出向量
 *
 */

double BPNN::learn(const vd& _in, const vd& out)
{
    // 首先计算
    compute(_in);
    // 根据计算结果更新权值
    // 计算误差项
    double error=0;
    for(int i = 0; i < num_out; ++i)
        delta_out[i] = sigmoid_d(vec_out[i]) * (out[i] - vec_out[i]),
            error += std::abs(delta_out[i]);
    for(int i = 0; i < num_hid; ++i)
    {
        delta_hid[i] = 0;
        for(int j = 0; j < num_out; ++j)
            delta_hid[i] += hid_out[j][i] * delta_out[j];
        delta_hid[i] *= sigmoid_d(vec_hid[i]);
        error+=std::abs(delta_hid[i]);
    }
    // 更新网络权值
    double d_ij;
    for(int i = 0; i < num_out; ++i)
        for(int j = 0; j < num_hid; ++j)
        {
            d_ij = learn_rate * delta_out[i] * vec_hid[j] + momentum * pre_hid_out[i][j];
            hid_out[i][j] += d_ij;
            pre_hid_out[i][j] = d_ij;
        }
    for(int i = 0; i < num_out; ++i)
        const_hid[i] += learn_rate * delta_out[i];

    for(int i = 0; i < num_hid; ++i)
        for(int j = 0; j < num_in; ++j)
        {
            d_ij = learn_rate * delta_hid[i] * vec_in[j] + momentum * pre_in_hid[i][j];
            in_hid[i][j] += d_ij;
            pre_in_hid[i][j] = d_ij;
        }
    for(int i = 0; i < num_hid; ++i)
        const_in[i] += learn_rate * delta_hid[i];

    return error;
}

小结

作者个人感觉，该算法描述相对简单，但其中包含的数学原理则很难讲述，实际上，作者在阅读了数遍之后，依然没有把概念讲清楚，详细内容建议读者参考《机器学习》（Tom M. Mitchell），这是一本很不错的书。
源代码在这里 在Readme中介绍了如何使用该算法识别手写的数字，由于数据集是以二进制形式给出的，作者并未查看数据集的数字是什么样的，如果读者可以创建自己的手写数字数据集的话，可以试一试学习效果，只不过图片的读取需要一定的知识。