计算机图形学：曲线曲面基本理论

1.几何造型介绍及曲线曲面的参数表示

1.1.几何造型介绍

计算机图形学可以分为三大部分内容，分别是光栅图形显示、几何造型技术和真实感图形显示。
①光栅图形学就是研究如何通过计算机的光栅显示屏来显示图形的方法，是图形学的基础。
②几何造型技术是研究在计算机中如何表达物体模型的技术。描述物体的模型可以分为线框模型、曲面模型和实体模型。线框模型通过顶点和棱边来表示物体曲面模型只描述物体的表面之间的连接关系，而不描述物体内部的点的属性。
③实体模型不但对物体的外观进行描述同时也描述物体的内点。
随着计算机图形学的发展，当前的主流是曲面模型，因此将其作为本章学习的重点。

1.2.曲线曲面的参数表示

1.2.1.曲线的非参数表示
曲线的非参数表示可以分为显式表示和隐式表示。
①对于平面曲线，其显示表示的方程如下：

在显式方程中一个x值和一个y值相对应，因此显式方程不能表示封闭或多值的平面曲线。
②平面曲线的隐式表示是指将平面曲线写成f(x,y)=0的形式。隐式表示的优点在于能够快速判断一个点是否在曲线上，但是隐函数表示不方便作图。
尽管被我们熟悉，但是非参数方程会有如下一些问题：首先方程与坐标轴相关（需要同时涉及两个以上的坐标轴）其次会产生斜率为无穷大的情况。考虑到非参数方程的这些不足之处，我们在图形学中需要考虑使用其他的表示方法。
1.2.2曲线的参数表示
如果平面曲线的各坐标均写成关于另一个参数t的函数，就可以得到如下图所示的曲线表示形式，该表示形式就是曲线的参数表示。这样，给定一个参数t的值，就可以得到曲线上一个点的坐标。

类似的，可以对空间曲线进行参数表示：

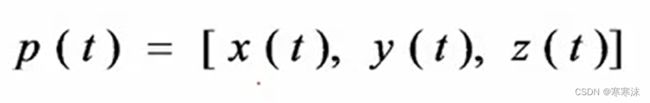
假设参数t的取值区间为[a,b]，为了方便起见，常常把区间[a,b]进行规范化，也就是将[a,b]区间转化为[0,1]，变换的方法为：

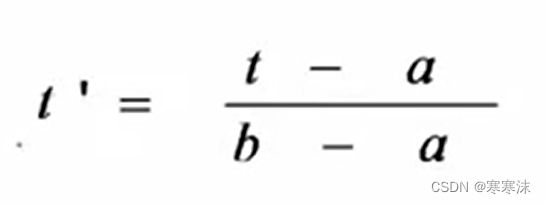
经过变换后的曲线可以写成如下形式：

最简单的参数曲线是直线段，其表示方法为如下图所示（其中p表示一个点的各个坐标轴的坐标值）

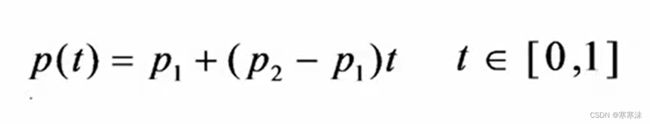
1.2.3.曲面的参数表示
与曲线的参数表示类似，曲面的参数表示要比曲线多一个参数，形式如下图所示：

2.参数曲线的基本概念

一条用参数表示的空间曲线是一个有界点集，可以写成如下所示的数学函数形式：

关于参数曲线，在微分几何中有一些重要的量定义如下：

1.位置矢量：用于描述空间曲线上任意一点的位置，可以表示为如下形式：

2.切矢量：对位置矢量求导后的结果，表示空间曲线在某点处的切线；
3.曲率：对单位切向量再次进行求导所得到的向量。曲率的几何意义是该点处曲线的弯曲程度，曲率越大，弯曲程度越大。曲率的倒数称为曲率半径。
4.法矢量：与切矢量垂直的向量。法向量的图示如下：
（N表示切向量，T表示法向量，将B称为副法向量）

将N和B构成的平面称为法平面（与法线垂直的平面），将N和T构成的平面称为密切面，将N和B构成的平面称为从切面。切向量、主法向量和副法向量构成了曲线上的活动坐标系。
5.挠率：由于空间曲线不仅要弯曲，还会发生扭曲（也就是不只在一个xOy坐标面发生弯曲，在xOz坐标面也会发生弯曲），因此用挠率这一个量来表述曲线的扭曲程度。
6.插值：给定一组有序的数据点，构造一条曲线使得曲线能按照顺序依次经过这些数据点，则称该曲线为插值曲线。把曲线插值推广到曲面，就可以得到类似的插值曲面。构造插值曲线和插值曲面所采用的数学方法称为曲线曲面插值法。
常用的插值方法有线性插值和抛物线插值。
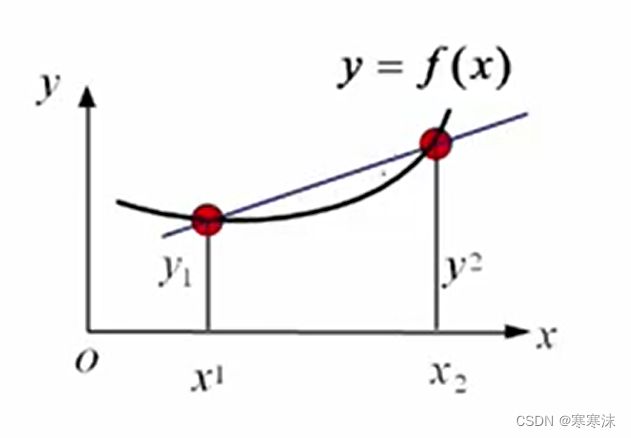
线性插值：给定两个点的坐标值，接着用一条直线将两个点连接起来，该直线的方程就称为线性插值函数，如下图所示：
（f(x)为真实函数，插值函数是图中的蓝色直线）

抛物线插值：给定三个点的坐标，用一个抛物线将三个点连接起来，该抛物线的方程就称为抛物线插值函数，如下图所示：
（f(x)为真实函数，Ψ(x)为抛物线拟合函数）

7.拟合：拟合是指构造一条在某种意义下最接近给定的所有数据点的曲线（但未必通过数据点），所构造的曲线称为拟合曲线。
由于离散点的测量本身就存在误差，而此时使用插值方法就显得不太方便，因此在数据点较多时可以选用拟合的方式。
8.逼近：逼近指用一些性质较好的函数来近似表示一些性质不太好的函数，插值和拟合都可以视为逼近的方法。
对于逼近所得到的曲线，连接数据点的折线通常被显式出来（如下图所示），用来题型设计者控制点的次序。将连接有一定次序控制点的折线称为控制多边形或特征多边形。
9.光顺：曲线的拐点（凸曲线和凹曲线的交点）不能太多。对于平面曲线，其相对光顺的条件：①具有二阶几何连续性（几何连续性请见文章后面的定义）②曲线的拐点较少；③曲线的曲率变化较为平缓。
10.连续性：曲线的连续性按意义进行划分可以分为参数连续性和几何连续性。

3.参数曲线的连续性

3.1参数连续性：

①0阶参数连续性（C0）：曲线的几何位置连续，也就是每两个相邻的曲线段在端点处相交。
②1阶参数连续性（C1）：在满足C0的前提下，曲线的斜率连续，也就是每两个相邻的曲线段在端点处的导数相同。
③2阶参数连续性（C2）：在满足C1的前提下，曲线的交点处的二阶导数相同。
类似地，可以定义更高阶次的参数连续性。但是，参数连续性在计算机图形学中由于要求过于苛刻因此不太适合使用，由此引入了下面几何连续性的概念。

3.2几何连续性：

①0阶几何连续性（G0）：与C0相同。
②1阶几何连续性（G1）：两条曲线在交点处满足G0的条件下，两条曲线在交点处的导数成比例。
③2阶几何连续性（G2）：两条曲线在满足G1的前提下有公共的曲率。
参数连续意味着切向量的方向和大小均相同，但是几何连续只要求切向量的方向相同，但是长度可以不同，因此条件减弱了。因此实际应用中常使用几何连续性。

4.参数化及曲线的代数形式和几何形式

4.1.参数化

①过给定的多个数据点可以构造多个插值多项式。对于一组有序的型值点所确定的一种参数分割称为这组型值点的参数化。下面举一个例子：
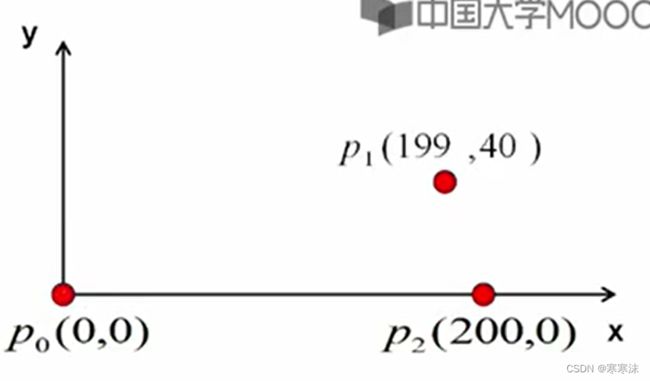
假设有三个型值点(0,0) (100,50) (200,0)，并假设确定三个点的对应参数t分别为0,0.5和1，请确定一个二次多项式作为这三个点的插值函数。设置三个型值点对应参数0,0.5和1的过程就是参数化。
②参数化要尽可能科学，也就是参数化要尽可能符合型值点之间的位置关系，比如下图中，如果取t=0,t=0.5和t=1这一组参数就不太科学（因为p1和p2两个点挨得很近）。
③常用的参数化方法有均匀参数化和累加弦长参数化等。

4.2.曲线的代数形式和几何形式

①参数曲线的代数形式：代数表达式如下所示：

代数形式直观明了，但是不太方便反映系数曲线的变化情况，因此在图形学中更多采用参数曲线的几何形式。
②参数曲线的几何形式：几何形式是利用曲线端点的几何性质来刻画一条曲线。端点的几何性质指的是端点的位置矢量、切向量以及各阶导数等。
对三次参数曲线，需要使用到其端点的两个函数值和两个导数值来描述这条曲线。假设两个端点的坐标分别为P0和P1，导数值分别为P0’和P1’，设参数曲线方程如下所示：

则可计算得到各次项的系数为：

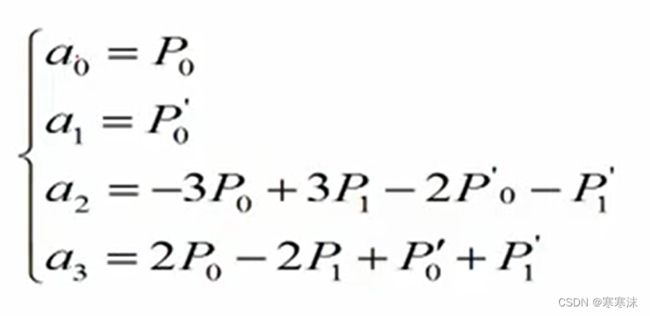
由此可以得到最终结果为：

此结果实际上就是三次Hermite曲线的几何形式。

5.贝塞尔曲线的背景与定义

5.1.贝塞尔曲线背景

当用曲线段拟合曲线时，可以把曲线表示为许多小线段之和，其中每个小线段的方程称为基函数，则曲线可以表示为如下形式：（其中前一项为矢量系数，后一项为基函数，矢量系数是首尾相接的）。综合准确性和方便程度的综合考虑，常常使用多项式作为基函数。

1962年，法国雷诺汽车公司的工程师贝塞尔完成了一套以逼近为基础的参数曲线和参数曲面的设计方法。贝塞尔曲线的基本思想是：首先用折线段勾画出物体的大致轮廓，再用光滑的参数曲线来逼近这个折线多边形，用来逼近的曲线就称为贝塞尔曲线。
贝塞尔给出的基函数如下，称为贝塞尔基函数：

贝塞尔基函数非常复杂，后来有人证明贝塞尔基函数可以简化为伯恩斯坦基函数，使得贝塞尔曲线得到了广泛的应用。伯恩斯坦基函数如下：

5.2.贝塞尔曲线定义

贝塞尔曲线的参数方程如下：

其中p是控制多边形的顶点，B表示的是伯恩斯坦基函数，伯恩斯坦基函数的计算方式为：

随着t从0到1发生变化，所计算出的点的位置也会发生变化，这些点共同组成了一条空间中的曲线，也就是贝塞尔曲线。

5.3.贝塞尔曲线举例

①一次贝塞尔曲线：就是连接两个顶点的直线段，其参数方程表示为：

②二次贝塞尔曲线：二次贝塞尔曲线的表达式如下：

③三次贝塞尔曲线：三次贝塞尔曲线的表达式如下：

贝塞尔曲线不能对曲线的局部形状进行控制，如果改变任意一个控制点的位置整个曲线都会受到影响。

6.贝塞尔曲线性质

6.1.伯恩斯坦基函数性质

①非负性：只有在参数t=0或者1时才为零，其他t取值情况下都是正数。
②权性：基函数共有n+1个，这些基函数相加的和刚好为一。
③对称性：如果保持n次贝塞尔曲线控制多边形1顶点位置不变而颠倒次序，此时曲线仍然不变但是走向相反。
④递推性：n次的伯恩斯坦基函数可以由两个n-1次的伯恩斯坦基函数经过线性组合得到。可以用递推性来对伯恩斯坦基函数进行降阶。

6.2.贝塞尔曲线性质

①端点性质：贝塞尔曲线经过且仅经过控制多边形的第一个和最后一个顶点。
②一阶导数：贝塞尔曲线在起点和终点处的导数值分别为：


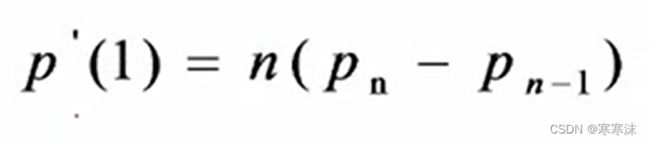
③几何不变性：贝塞尔曲线的形状只与各个顶点的相对位置有关而与坐标系的选择无关。
④变差缩减性：如果贝塞尔曲线的特征多边形是一个平面图形，则平面内任何直线与贝塞尔曲线的交点个数小于等于该支线与特征多边形的交点个数。此性质反映了贝塞尔曲线比其特征多边形的波动更小，也就是贝塞尔曲线比其特征多边形更加光顺。

7.贝塞尔曲线的生成方法

生成贝塞尔曲线实际上就是要求出曲线上的点，有两种生成方法。
第一种方法是根据定义直接生成贝塞尔曲线，其关键是求出伯恩斯坦基函数。由于计算递归等步骤非常消耗时间，因此效率较为低下。
第二种方法是曲线的递推算法（de Casteljau算法），该方法的效率要远远高于定义法求贝塞尔曲线。
递推算法的步骤为：贝塞尔曲线上的任一点，都是由其他相邻线段的同等比例t处的连线，再取同等比例t进行连线，直到最后一条线段的同等比例t处的点。
举例说明：求二次贝塞尔曲线上t=1/3的点。


算出图中各个点的参数表达式为：

由上面推理可得贝塞尔曲线的递推公式为：

递推算法由于直观简便并且稳定可靠，因此是生成贝塞尔曲线的基本算法和标准算法。

贝塞尔曲线绘制代码（C++）

自写的贝塞尔曲线绘制代码如下

#include
#include
#include
#include
#include
using namespace std;

void GetBezier(const int* xArray, const int* yArray, const unsigned& n)
{
	initgraph(1000, 700);
	for (int i = 0; i < n - 1; i++)
	{
		fillcircle(xArray[i], yArray[i], 3);
		line(xArray[i], yArray[i], xArray[i + 1], yArray[i + 1]);
	}
	fillcircle(xArray[n - 1], yArray[n - 1], 3);
	_getch();
	for (float t = 0; t <= 1; t += 0.001)
	{
		vector<double>xvec, yvec;
		for (unsigned i = 0; i < n; i++)
		{
			xvec.push_back(xArray[i]);
			yvec.push_back(yArray[i]);
		}
		for (unsigned Current_PointNum = n; Current_PointNum > 1; Current_PointNum--)
		{
			for (unsigned i = 0; i < Current_PointNum - 1; i++)
			{
				xvec[i] = (1 - t) * xvec[i] + t * xvec[i + 1];
				yvec[i] = (1 - t) * yvec[i] + t * yvec[i + 1];
			}
		}
		putpixel(xvec[0], yvec[0], GREEN);
		Sleep(1);
	}
	_getch();
	closegraph();
	return;
}

int main(void)
{
	unsigned pointNum;
	cout << "请输入控制多边形点的个数：";
	cin >> pointNum;
	int* xArray = new int[pointNum];
	int* yArray = new int[pointNum];
	cout << "请分别输入各个点的横纵坐标值：" << endl;
	for (int i = 0; i < pointNum; i++)
	{
		cin >> xArray[i] >> yArray[i];
	}
	cout << "参数确认完毕，按任意键开始绘图..." << endl;
	_getch();
	GetBezier(xArray,yArray,pointNum);
	return 0;
}

绘制结果如下：