【机器学习算法面试题】四.深度神经网络中激活函数有哪些?
文章目录
- 1.Sigmoid型函数
-
- 1.1.Logistic函数
- 1.2.Tanh函数
- 1.3.Hard-Logistic函数
- 1.4.Hard-Tanh函数
- 2.整流线性单元(ReLU)函数
-
- 2.1.ReLU函数
- 2.2.Leaky ReLU函数
- 3.面试题
相关笔记链接:
【机器学习算法面试题】一.准确率Accuracy的局限性。
【机器学习算法面试题】二.精确率Precision和召回率Recall的权衡。
【机器学习算法面试题】三.数据处理时应如何处理类别型特征?
【机器学习算法面试题】四.深度神经网络中激活函数有哪些?
【机器学习算法面试题】五.在模型评估过程中,过拟合和欠拟合具体是指什么现象?
【机器学习算法面试题】六.训练集、验证集、测试集的理解。
【机器学习算法面试题】七.如何进行线上A/B测试,如何划分实验组和对照组?
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
1.Sigmoid型函数
Sigmoid型函数是指一类S型曲线函数(通俗理解就是曲线的图像字母"S"),为两端饱和函数。常用的Sigmoid型函数有Logistic函数和Tanh函数。
饱和函数的理解:当自变量x到达一定值以后,因变量f(x)不再发生变化或趋近于某个值。
两端饱和函数的理解:自变量x趋近于+∞时,因变量f(x)不不再发生变化或趋近于某个值;自变量x趋近于-∞时,因变量f(x)不不再发生变化或趋近于某个值。
个人理解: 在部分书籍或者说法中,Sigmoid函数应该是特指的是Logistic函数。
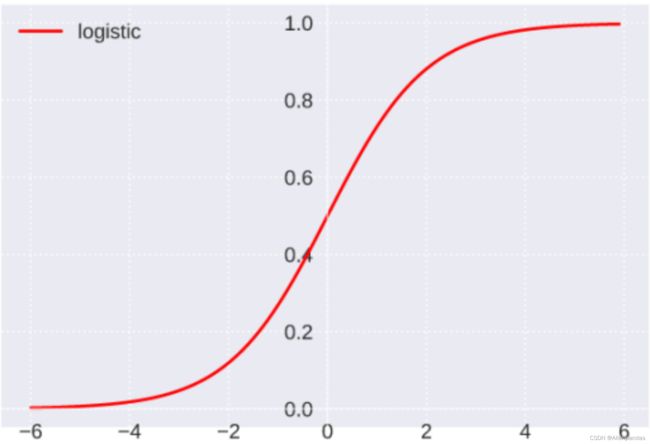
1.1.Logistic函数
公式:
σ ( x ) = 1 1 + exp ( − x ) \sigma(x) = \frac{1}{1+\exp (-x)} σ(x)=1+exp(−x)1
函数值域: (0, 1)
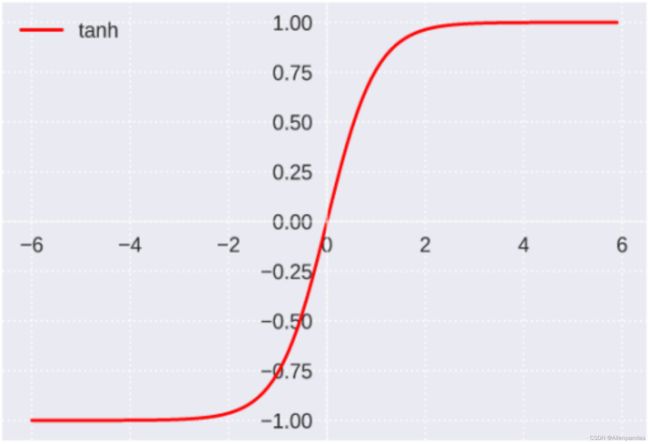
1.2.Tanh函数
公式:
tanh ( x ) = exp ( x ) − exp ( − x ) exp ( x ) + exp ( − x ) \tanh (x)=\frac{\exp (x)-\exp (-x)}{\exp (x)+\exp (-x)} tanh(x)=exp(x)+exp(−x)exp(x)−exp(−x)
函数值域: (-1, 1)
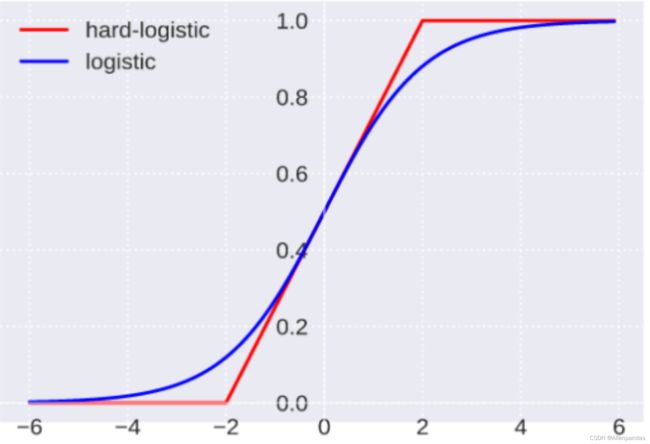
1.3.Hard-Logistic函数
Hard-Logistic函数是对Logistic函数的分段近似,并且可以取到端点的值。
公式:
hard-logistic ( x ) = max ( min ( 0.25 x + 0.5 , 1 ) , 0 ) \text { hard-logistic }(x)=\max (\min (0.25 x+0.5,1), 0) hard-logistic (x)=max(min(0.25x+0.5,1),0)
函数值域:[0, 1]
1.4.Hard-Tanh函数
Hard-Tanh函数是对Tanh函数的分段近似,并且可以取到端点的值。
公式:
hard-tanh ( x ) = max ( min ( x , 1 ) , − 1 ) \text { hard-tanh }(x)=\max (\min (x, 1),-1) hard-tanh (x)=max(min(x,1),−1)
函数值域: [-1, 1]
2.整流线性单元(ReLU)函数
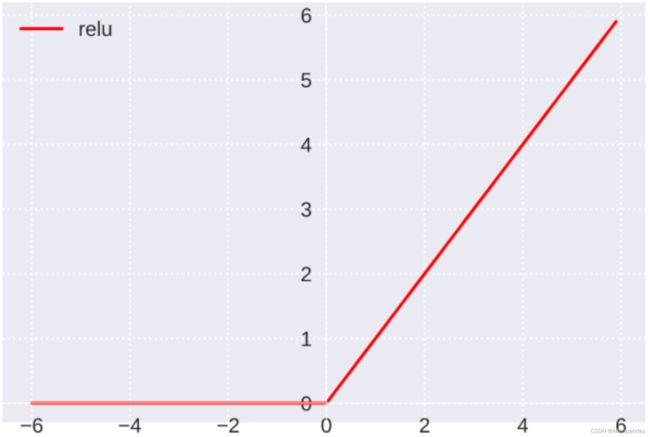
2.1.ReLU函数
公式:
ReLU ( x ) = { x , x ≥ 0 0 , x < 0 = max ( 0 , x ) \operatorname{ReLU}(x)=\left\{\begin{array}{ll} x, & x \geq 0 \\ 0, & x<0 \end{array}=\max (0, x)\right. ReLU(x)={x,0,x≥0x<0=max(0,x)
函数值域:(0, +∞)
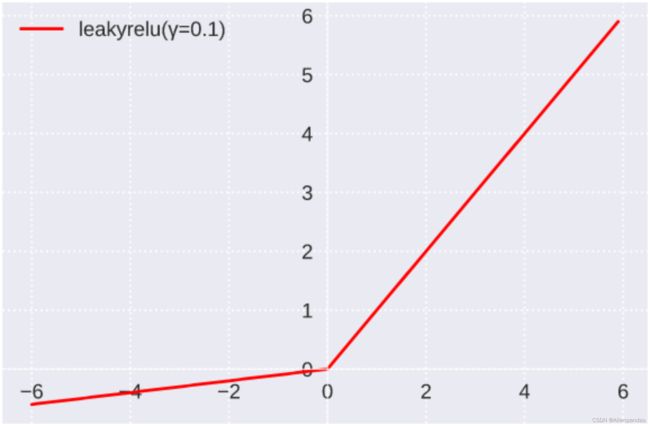
2.2.Leaky ReLU函数
公式:
LeakyReLU( x ) = { x , x ≥ 0 γ x , x < 0 = max ( 0 , x ) + γ min ( 0 , x ) \text { LeakyReLU( } x \text { ) }=\left\{\begin{array}{ll} x, & x \geq 0 \\ \gamma x, & x<0 \end{array}=\max (0, x)+\gamma \min (0, x)\right. LeakyReLU( x ) ={x,γx,x≥0x<0=max(0,x)+γmin(0,x)
函数值域:(﹣∞, ﹢∞),γ是超参数
3.面试题
题目: 在某神经网络的隐层输出中,包含-1.5,那么该神经网络采用的激活函数不可能是()
A.sigmoid B.tanh C.relu
答案: ABC
解析:
A.sigmoid函数(特指Logistic函数)的值域为(0, 1)
B.tanh函数的值域为(-1, 1)
C.relu函数的值域为[0, ﹢∞)
所以ABC都不可能。
题目: 在某神经网络的隐层输出中,包含0.75,那么该神经网络采用的激活函数可能是()
A.sigmoid B.tanh C.relu
答案: ABC
解析:
A.sigmoid函数(应该是特指的Logistic函数)的值域为(0, 1)
B.tanh函数的值域为(-1, 1)
C.relu函数的值域为[0, ﹢∞)
所以ABC都可能。