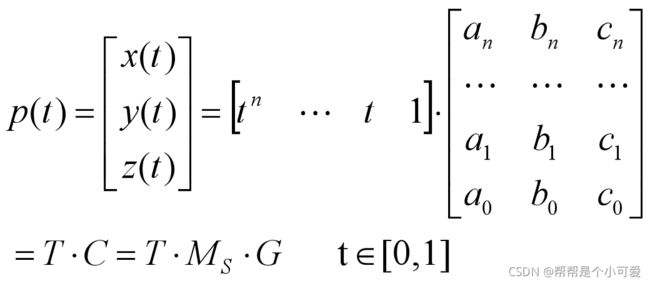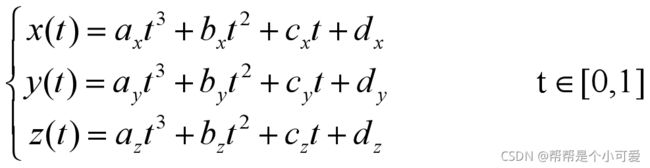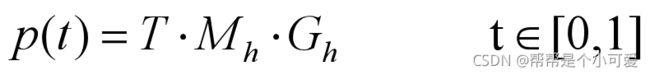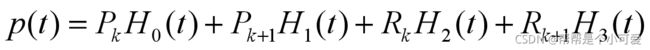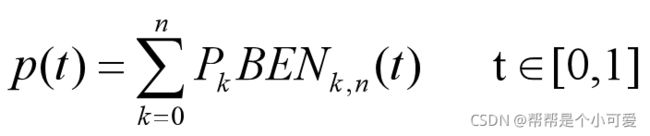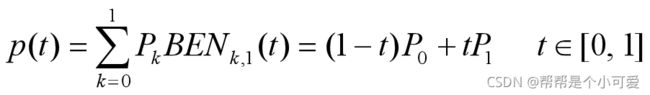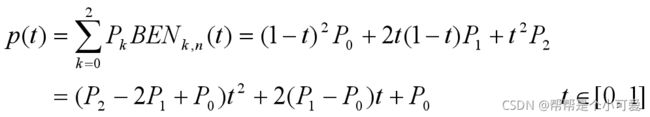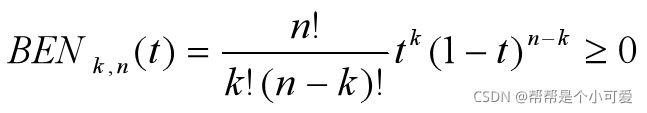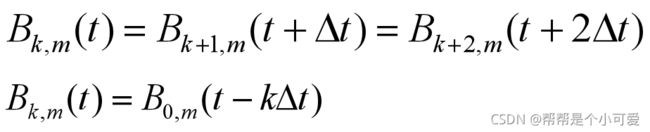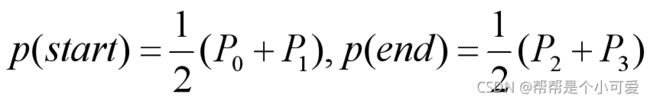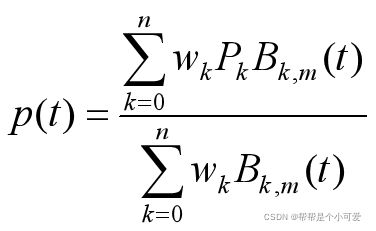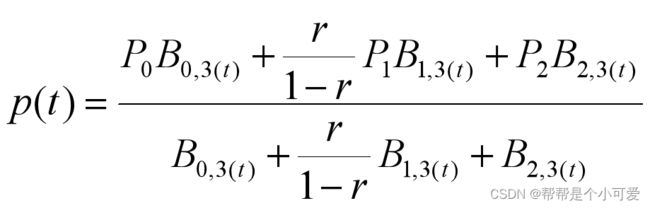计算机图形学-曲线和曲面

8.1基本概念 8.2三次样条 8.3Bezier曲线曲面 8.4B样条曲线曲面 8.5有理样条曲线曲面

一、曲线曲面数学描述的发展

弗格森双三次曲面片 （形状控制与连接问题）

孔斯双三次曲面片 （形状控制与连接问题）

样条方法 （解决插值问题，无局部调整的自由度，形状难以预测）

Bezier方法 （连接和局部修改问题）

B样条方法 （解决局部控制、连接问题，局部控制方便，形态灵活直观）

有理Bezier 

非均匀有理B样条方法

1991 NURBS标准 定义工业产品几何形状的唯一数学方法

二、曲线曲面的表示要求

唯一性 从已有信息得到的图形唯一

几何不变性 形状不随坐标系改变而改变。通常标量函数没有几何不变性，二参数曲线/曲面在某些情况下有。

易于定界 参数法易于定界

统一性 统一表示和处理各种曲线曲面情况（兼容度高）

易于实现光滑连接

几何直观 

三、曲线曲面的表示

关于参数法

特点：更满足形状数学描述要求

点动成线；

具有几何不变性；

通过对参数求导代替斜率，避免斜率无穷大

dy/dx = (dy/dt)/(dx/dt)

几何分量有界：t∈[0,1]；

对方程直接仿射和投影

将自变量和因变量分开，明显的表示参数变化对变量的影响

四、插值与逼近

样条：模线样表法表示和传递自由曲面的形状

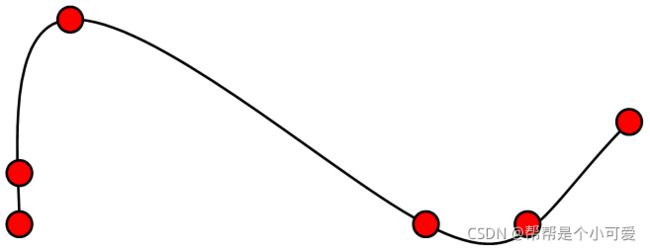
样条曲线：由多项式曲线段连接成的曲线，在边界处满足特定的连续条件

样条曲面：用两组正交样条曲线表示

型值点与曲线曲面的拟合：用一组型值点来指定曲线曲面的形状时，形状完全通过给定的型值点列

控制点与曲线曲面的逼近：用一组控制点来指定曲线曲面的形状时，求出的形状不必通过控制点列

（拟合 与 逼近）

   

求给定型值点之间曲线上的点称为曲线的插值。

控制/特征多边形：将连接有一定次序控制点的直线序列称为控制多边形或特征多边形，例如有图中的虚线部分。

五、连续性条件

假定参数曲线段pi以参数形式进行描述

参数连续性：

0阶参数连续性，记作Cº连续性，是指相邻曲线的对应几何位置连接

1阶参数连续性，记作C¹连续性，指代表两个相邻曲线段的方程在相交点处有相同的一阶导数

2阶参数连续性，记作C²连续性，指两个相邻曲线段的方程在相交点处具有相同的一阶和二阶导数

对于C²连续性，交点处的切向量变化率相同，曲线段之间平滑变化。

几何连续性：（相对于参数连续性，只需成比例即可）

0阶几何连续性，记作Gº连续性，与0阶参数连续性的定义相同，对应连接

1阶几何连续性，记作G¹连续性，指一阶导数在相邻段的交点处成比例

2阶几何连续性，记作G²连续性，指相邻曲线段在交点处其一阶和二阶导数均成比例

六、样条描述

对于给定了控制点位置的样条参数曲线，需要给出对应的样条描述，以唯一确定这条曲线。

对于一条三维的n次样条参数多项式曲线的矩阵：

矩阵形式：

 

其中的T是关于参数t的幂次行向量矩阵(1 x（n+1）)，C是系数矩阵(（n+1）x 3).

系数矩阵C：

C = MsG

G是包含样条形式的几何约束条件的（n+1）x 3阶矩阵，Ms是一个（n+1）x（n+1）阶矩阵，又称为基矩阵，将几何约束值转化成多项式系数，提供样条曲线的特征。

最后得到的样条参数多项式曲线的矩阵表达式：

P(t) = TMsG

七、三次样条

1）给定n+1个控制点，可得到通过每个点的分段三次多项式曲线

t为参数；t=0对应起点，t=1对应终点。n+1个控制点会生成n条三次样条曲线段

2）自然三次样条

三次参数样条曲线具有C²连续性

 给定n+1个型值点，现通过这些点列构造一条自然三次参数样条曲线，要求在所有曲线段的公共连接处均具有位置、一阶和二阶导数的连续性，即自然三次样条具有C2连续性。

还需要两个附加条件解方程组。

 特点：适应于型值点分布比较均匀的场合，不能“局部控制”，即不能仅改变其中的一段而不改变其他部分

3）三次Hermite样条

定义：假定型值点Pk和Pk+1之间的曲线段为P(t),t∈[0,1]，给定矢量Pk、Pk+1、Rk和Rk+1，则满足下列条件的三次参数曲线为三次Hermite样条曲线：

p(0)  = Pk

p(1)  = Pk+1

p'(0)  = Rk

p'(1)  = Rk+1

三次Hermite样条曲线的方程为：

其中的Mh是Ms边界约束矩阵的逆矩阵；Gh是曲线型值点及其切矢的矩阵。

 通常将T•Mh称为Hermite基函数（混合函数，调和函数），各分量为：

只要给定Gh就可以求出P(t)

特点：

可以局部调整，因为每个曲线段仅依赖于端点约束

基于Hermite样条的变化形式：Cardinal样条和Kochanek-Bartels样条

Hermite曲线具有几何不变性

八、Bezier曲线曲面（面向几何的）

也是参数多项式曲线，由一组控制多边形曲线的顶点唯一定义。

控制多边形的各顶点只有第一个和最后一个在曲线上。

要增加某段曲线的阶次，仅需指定另一个中间顶点。

1）定义：对于有 n+1 个控制点的Bezier曲线段：

Bernstein基函数具有如下形式：（公式类似二项式定理）

 （假设当k=0，t=0时，tk=1，k!=1）

Bezier曲线是阶数比控制点少1的多项式

关于一/二/三阶Bezier曲线的表达式：

一次Bezier曲线（n=1）两个控制点，一次多项式

二次Bezier曲线（n=2）三个控制点，二次多项式

三次Bezier曲线（n=3）四个控制点，三次多项式

 BENk,n(t)是三次Bezier曲线的基函数，他们各自都是三次曲线，任何三次Bezier曲线都是他们的线性组合。

 

 2）Bezier曲线的性质

 1.函数值、导数值和切线

端点和端点函数值

p(0) = P0

p(1) = Pn

所以Bezier曲线总是通过起点和终点。

 一阶导数

p'(0) = n(P1 - P0)

p'(1) = n(Pn - P(n-1))

 所以Bezier曲线在起点处的切线位于前两个控制点的连线上，终点处的切线位于后两个控制点的连线上，即：起点和终点处的切线方向与起始和终止折线段的切线方向一致。

 二阶导数

 Bezier曲线在起始点和终止点处的r阶导数分别取决于起始点或终止点以及最开始和最后的r个控制点

2.对称性

 保持控制多边形的顶点位置不变，仅仅把它们的顺序颠倒一下，将下标为k的控制点Pk改为下标为n-k的控制点Pn-k时，曲线保持不变，只是走向相反而已。

3.凸包性

 

 

t在0~1变化时，对于任一t值，基函数均为正，各项之和恒为1

 Bezier曲线各点均落在控制多边形各顶点构成的凸包（包含所有顶点的最小凸多边形）之中

 Bezier曲线的凸包性保证了曲线随控制点平稳前进而不会振荡

 4.几何不变性

曲线形状仅与控制多边形的顶点相对位置有关，与坐标系选择无关

5.差变减少性

如果控制多边形是平面图形，平面内任意直线与曲线交点数不多于直线与控制多边形的交点个数；推广至空间成立。

反映的是曲线比控制多边形波动少。

6.控制顶点变化对曲线形状的影响

移动n次Bezier曲线的第i个控制点Pi，会在曲线上参数为t = i/n 的点 P(i/n) 处发生最大影响。因为相应的基函数在此处达到最大值。

3）Bezier曲面

 双三次曲面（略 P45 46）

性质

控制网格的四个角点正好是Bezier曲面的四个角点

控制网格最外一圈顶点定义Bezier曲面的四条边界，这四条边界均为Bezier曲线

几何不变性、对称性、凸包性等

4）不足

 控制多边形的顶点个数决定了Bezier曲线的阶数，且当顶点个数较大时，控制多边形对曲线的控制将会减弱；

 不能作局部修改，任何一个控制点位置的变化对整条曲线都有影响。

九、B样条曲线曲面

1）定义

 

 

 参数：

m是曲线的阶参数，(m-1)为B样条曲线的次数，曲线在连接点处具有(m-2)阶连续性

tk是结点值，T＝（t0，t1，…tn＋m）构成了m－1次B样条函数的节点矢量

结点矢量分为三种类型：均匀的，开放均匀的和非均匀的。B样条曲线的分类同理。

2）均匀周期性B样条曲线

结点沿参数轴均匀等距分布，即tk+1－tk=常数时，所生成的曲线称为均匀B样条曲线

基函数呈周期性。

例：

均匀二次（三阶）B样条曲线

关于起点和终点：

 对于由任意数目的控制点构造的二次均匀周期性B样条曲线来说，曲线的起始点位于头两个控制点之间，终止点位于最后两个控制点之间。

  对于高次多项式，起点和终点是m－1个控制点的加权平均值点。若某一控制点出现多次，样条曲线会更加接近该点。

/*

**********

曲线的起点和终点：

 均匀二次B样条曲线起点和终点处的导数：

***********

*/

三次周期性B样条曲线

取m=4，n=3，节点矢量为：T=(0,1,2,3,4,5,6,7)：

 

 

 注意上面两张图矩阵和多项式系数的对应5）

3）开放均匀B样条曲线

在两端的结点值重复m次。可以看成特殊的均匀/非均匀B样条曲线。

具有与bezier相似的特征，当m = n+1 时，开放b样条曲线就是Bezier曲线。

当P0 = Pk时，生成封闭的曲线。

曲线起终点的切线与对应控制点连线平行。

十、B样条曲线性质

1.局部支柱性

B样条函数与Beizer的主要区别：基函数是否分段。

 基函数是分段函数，在参数变化范围内，每个基函数在tk到tk+m的子区间内函数值不为零，在其余区间内均为零，通常也将该特征称为局部支柱性。

好处：

1）第k段曲线只由m个控制点组成（t ∈ [ tk,tk+1 )，m-1 ≤ k ≤m）;要修改曲线，只需修改这m个控制顶点。

 2）修改控制顶点Pk对曲线的影响是局部的。对于均匀m次B样条曲线，调整一个顶点Pk的位置只影响B样条曲线在区间 [ tk,tk+1 ) 的部分，最多影响与该顶点有关的m段曲线。

2.凸组合性质

凸包性的进阶版：

B样条基函数的数值均大于等于0，他保证了B样条曲线的凸包性，B样条曲线必须处在控制多边形形成的凸包之内。同时，曲线的第k段处于m个对应的控制点形成的凸包内，整条B样条曲线位于各凸包的并集内。（较好的跟随性）

对比：

 3.连续性

若一结点矢量中结点均不相同，则m阶（m-1次）B样条曲线在结点处 m-2 阶连续。

B样条曲线的基函数次数与控制顶点个数无关。

存在重结点时：重结点处的连续性降低。结点的重复度为J，该处的连续性降低J阶。

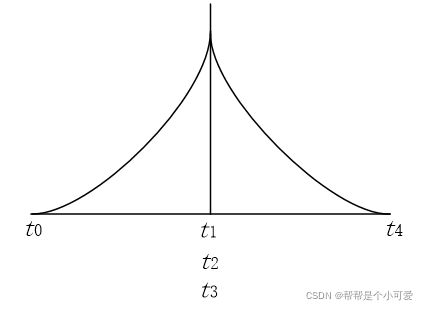
如图：具有三重结点（重复度为2）的三次B样条，结点t₁重复度为2，连续性降低2阶，仅保持连续。若重复度为3，曲线退化为离散的控制顶点。 

4.导数

B样条曲线的导数曲线是一条 m-1 阶的B样条曲线。

5.几何不变性

6.差变减少性

十一、B样条曲面

B样条曲线的二维拓展。

 控制顶点、控制网格（特征网格）、B样条基函数。 B样条曲面具有与B样条曲线相同的局部支柱性、凸包性、连续性、几何不变性等性质。

十二、有理样条曲线/曲面

NURBS曲线曲面

定义

 有理B样条的表达式

 取不同的r值得到各种二次曲线。

曲面：公式略

性质：普遍性 局部性 凸包性 可微性 权因子

特点：

为自由型曲线曲面、初等曲线曲面的精确表示与设计提供了公共的数学形式；一个统一的数据库就能够存储这两类形状信息

为了修改曲线曲面的形状，既可以借助调整控制顶点，又可以利用权因子，因而具有较大的灵活性

计算稳定速度快

明确的几何解释和强有力的几何配套工具

几何和透视投影变换不变性

NURBS是非有理B样条形式以及有理与非有理Bezier形式的合适的推广

权因子的不合适应用可能导致很坏的参数化，甚至毁掉随后的曲面结构

某些技术用传统形式比用NURBS工作得更好。例如，曲面与曲面求交时，NURBS方法特别难于处理刚好接触的情况

某些基本算法，例如求反曲线曲面上的点的参数值，存在数值不稳定问题

------------------------2021-11-30-23:27--------------------------