西瓜书学习第六章---SVM

一、间隔与支持向量

1.1 分类学习的基本思想

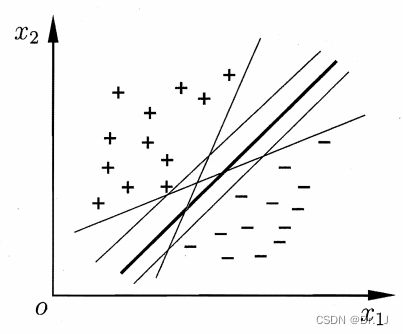
分类任务的基本思想是在给定的数据集上用一个超平面 $w^{T}x+b=0$将数据集分为两类，显然在一个线性可分的数据集上，能够做到这种效果的超平面有很多，如下图：

1.1 有多个可以完成分类任务的超平面

1.2 支持向量机的思想

1. 相关概念
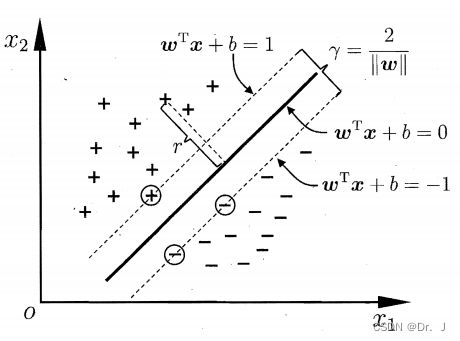
   支持向量： 距离超平面最近的若干训练样本，如下图在虚线上的正负样本
   间隔： 两个异类的支持向量到超平面的距离之和$\gamma =\frac{2}{||w||}$被称为间隔

1.2 支持向量和间隔的图解

2. 支持向量机的思想
   支持向量机（SVM）的目的就是在上述诸多超平面中找到一条泛化能力最好的，即离正负样本距离间隔最大的那一个超平面，如图1.2中的那一条黑线就是满足条件的，它对于新的样本点的抗干扰能力是最强的，在图1.1中其他超平面在识别处于正负样本分界线之内的新样本时错误率都会非常高

3. 数学原理
   3.1 超平面的分类数学原理
   在超平面的表达式$w^{T}x+b=0$中，$w=(w_1;w_2;...;w_d)$是超平面的法向量，它所决定是超平面的方向，$b$是偏置项，决定了超平面和原点之间的距离，所以$w和b$两个参数可以确定一个超平面，而设样本点到超平面的距离$r=\frac{|w^{T}x+b|}{||w||}$
   所以给定一个样本（$x_i,y_i$）,当一个超平面可以将样本正确分类时，有
   $$\{\begin{array}{ll}& {\text{w}}^{T}x+b\ge +1,y_i=+1;\\ & {\text{w}}^{T}x+b\le +1,y_i=-1\end{array}$$
   3.2 支持向量机的数学原理
   根据支持向量机的定义，要找到一个最大间隔的划分超平面，等价于求解能让$\gamma 最大的参数w和b$，即
   $$\begin{array}{r}\\ \underset{w,b}{\max }\frac{2}{||w||}\\ s.t.y_i\left(w^T{x}_i+b\right)\ge 1,i=1,2,..,m\end{array}$$
   为了求解方便，上式等价于最小化$||w|{|}^2$，即等价于
   $$\begin{array}{r}\\ \underset{w,b}{\min }\frac{1}{2}||w|{|}^2\\ s.t.y_i\left(w^T{x}_i+b\right)\ge 1,i=1,2,..,m\end{array}$$
   上式便是SVM的数学表达，显然它是一个二次凸优化问题

二、对偶问题

2.1 求解过程

本节主要讲述求解能够使$\gamma 最大的w和b$，使用的方法是拉格朗日算子法，能够得到SVM数学表达的对偶问题，即给每个约束条件增加一个拉格朗日乘子${\alpha }_i\ge 0$，所以根据SVM数学表示得到$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+{\sum }_{i=1}^m{\alpha }_i\left(1-y_i\left(w^T{x}_{i+b}\right)\right)$
然后$L$函数对$w和b$求偏导，可得到
$w={\sum }_{i=1}^m{\alpha }_i{y}_i{x}_i$
$0={\sum }_{i=1}^m{\alpha }_i{y}_i$
（详细计算结果见南瓜书对应章节）
将计算得到的$w和b代入到L$中就可以得到SVM数学表达的对偶问题
$$\underset{\mathbf{\alpha }}{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j$$
$$\begin{array}{ll}\text{ s.t. }& {\sum }_{i=1}^m{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\dots ,m\end{array}$$
显然，上述对偶问题的本质是一个二次规划问题，现在有很多高效的算法，比如SMO算法（详细介绍可见西瓜书p124）可以来解决二次规划问题，可以根据上述公式求得
$$\begin{array}{rl}f(\mathbf{x})& ={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i^{\mathrm{T}}\mathbf{x}+b\end{array}$$

2.2 KTT 条件

在2.1中所求解得到的${\alpha }_i$就是SVM原型中样本（$x_i,y_i$）的拉格朗日乘子，而且由于原式中有不等式的约束条件，所以在求解上述对偶问题时要遵循KTT 条件，即要满足如下不等式
$$\{\begin{array}{l}{\alpha }_i⩾0\\ y_{i}f\left({\mathbf{x}}_i\right)-1⩾0\\ {\alpha }_i\left(y_{i}f\left({\mathbf{x}}_i\right)-1\right)=0\dots \end{array}$$
所以根据上式能够看出SVM的一个性质，即在训练完毕之后，只需要保留支持向量就行，因为最早的模型只和支持向量有关系

三、核函数

3.1 核函数的作用

核函数$\kappa \left(\cdot ,\cdot \right)$的作用概括来说就是能够将低维的非线性可分的数据集变为高维的线性可分的数据集，如下图

3.1 非线性可分的异或问题经过变化之后成为了线性可分问题 可以证明，原始空间如果是有限维，那么一定有一个高维线性可分的特征空间对之对应

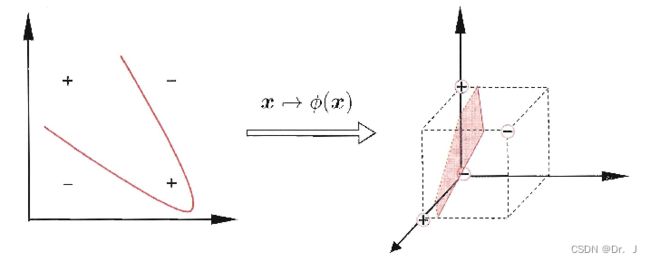
3.2 核函数作用的数学体现

1. 符号定义
   $\varphi (x)$ : $x$映射之后的特征向量
   $\kappa \left(\cdot ,\cdot \right)$：核函数的数学定义
   $f(x)=w^T\varphi (x)+b$：在映射空间的超平面模型表达

2. 计算过程
   第一步：首先将SVM原型改写为
   $$\begin{array}{rl}\underset{w,b}{\min }& \frac{1}{2}\Vert w{\Vert }^2\\ \text{ s.t. }& y_i\left(w^{\mathrm{T}}\varphi \left(x_i\right)+b\right)⩾1,i=1,2,\dots ,m\end{array}$$
   则能够得到对偶问题
   
   $\max {\sum }_{i=1}^m{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi {\left(x_i\right)}^{\mathrm{T}}\varphi \left(x_j\right)$
   
   $$\begin{array}{ll}\text{ s.t. }& {\sum }_{i=1}^m{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\dots ,m\end{array}$$
   第二步：使用核函数来对公式进行改写，（即$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=⟨\varphi \left({\mathbf{x}}_i\right),\varphi \left({\mathbf{x}}_j\right)⟩=\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)$）,可以得到如下改写：
   
   $$\begin{gathered} \underset{\mathbf{\alpha }}{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0 \\ {\alpha }_i⩾0,i=1,2,\dots ,m\text{. } \end{gathered}$$
   第三步：计算最终结果，可得
   $$\begin{array}{rl}f(\mathbf{x})& ={\mathbf{w}}^{\mathrm{T}}\varphi (\mathbf{x})+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi (\mathbf{x})+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\kappa \left(\mathbf{x},{\mathbf{x}}_i\right)+b\end{array}$$

3.3 常用的核函数

在进行映射的过程中，选择合适的核函数是非常重要的，下面是常用的一些核函数

名称	表达式	参数
线性核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j$
多项式核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\left({\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j\right)}^d$	$d\ge 1$为多项式的次数
高斯核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{{|{\mathbf{x}}_i-{\mathbf{x}}_j|}^2}{2{\sigma }^2}\right)$	$\sigma >0$为高斯核的带宽
拉普拉斯核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{|{\mathbf{x}}_i-{\mathbf{x}}_j|}{\sigma }\right)$	$\sigma >0$
Sigmoid核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\tanh \left(\beta {\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j+\theta \right)$	tanh为双曲正切函数，$\beta >0$,$\theta <0$

除了上述列出的核函数之外，还可以对两个或者更多的核函数进行几何变换得到新的核函数

四、软间隔和正则化

迄今为止我们所讨论的都是理想情况下，存在一个超平面可以将样本集完美的划分开，但是在实际生活中往往不存在如何完美的数据集，所以应该允许一些错误的出现，否则即使存在一个超平面对数据集进行了完美的划分，也可能是过拟合导致的，泛化能力依旧有问题，于是规定了软间隔的概念

4.1 软间隔的概念

与前面的硬间隔相对应，软间隔允许若干样本可以不满足硬间隔中的约束条件，但是这样的样本在最大化的过程中是要控制在一定数量之中的，所以原本SVM的数学模型可以改写为
$$\underset{\mathbf{w},b}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m{\ell }_{0/1}\left(y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)-1\right)$$

$${\ell }_{0/1}$$是损失函数，其表达式为
$${\ell }_{0/1}(z)=\{\begin{array}{ll}1,& \text{ if }z<0\\ 0,& \text{ otherwise }\end{array}$$
所以根据上式中能够看出，C越大，由于整个式子要趋于最小化，所以损失函数这一项就必须越小，相当于要求所以样本都满足SVM原式中的约束条件，反之，C为一个合适的取值时，就允许若干样本不满足约束

4.2 常用的损失函数

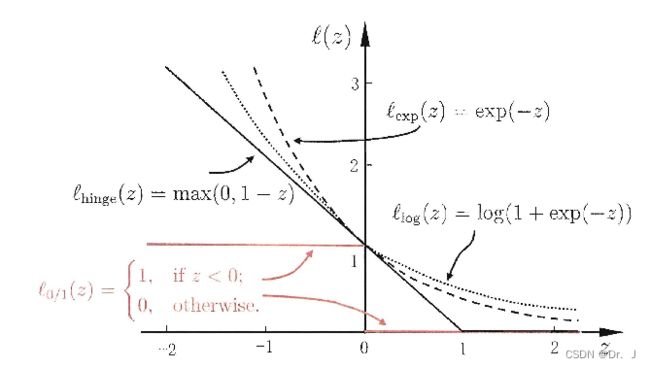
由于4.1中使用的0/1损失函数的数学性质并不好，所以通常使用一些连续的凸函数且取值都是0/1损失函数的上界，下表是常用的替代损失函数

名称	表达式
hinge损失函数	${\ell }_{\text{hinge }}(z)=\max (0,1-z)$
指数损失	${\ell }_{exp}(z)=\exp (-z)$
对率损失	${\ell }_{\log }(z)=\log (1+\exp (-z))$

下图是三种损失函数的函数图像：

4.1 常见替代损失函数的图像

在引入新的损失函数之后，定义松弛变量${\xi }_i\ge 0$，则可以得到如下公式，这个公式也是软间隔SVM的表达式
${\min }_{\mathbf{w},b,{\xi }_i}\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C{\sum }_{i=1}^m{\xi }_i$

$\begin{array}{ll}\text{ s.t. }& y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1-{\xi }_i\\ & {\xi }_i⩾0,i=1,2,\dots ,m.\end{array}$

则可以得到软间隔SVM的对偶问题：
$$\begin{array}{rl}\underset{\mathbf{\alpha }}{\max }& \sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j\\ \text{ s.t. }& \sum _{i=1}^m{\alpha }_i{y}_i=0\\ & 0⩽{\alpha }_i⩽C,i=1,2,\dots ,m\end{array}$$
且上式要满足的KTT 条件为
$$\{\begin{array}{l}{\alpha }_i⩾0,{\mu }_i⩾0\\ y_{i}f\left({\mathbf{x}}_i\right)-1+{\xi }_i⩾0\\ {\alpha }_i\left(y_{i}f\left({\mathbf{x}}_i\right)-1+{\xi }_i\right)=0\\ {\xi }_i⩾0,{\mu }_i{\xi }_i=0\end{array}$$

五、支持向量回归

支持向量回归简称SVR，是SVM在回归问题的一种运用，主要目的是学到一个类似于在分类问题中的$w^{T}x+b=0$的模型，如下图

5.1 支持向量的回归图，红色是间隔带

在上图中，如果训练样本落入到间隔带中，那就是预测正确，这就是SVR的基本思想，具体的计算思想和支持向量机是类似的，都是根据拉格朗日算子法将问题转换为对偶问题，在KTT 条件约束下进行计算求得模型，具体计算过程见西瓜书p135

六、核方法

核方法的基本概念就是指一系列的基于核函数的学习方法，其最基本也是使用最广泛的就是前面几章提到的用核函数将非线性数据集转换为线性可分的数据集，西瓜书上的本节主要是介绍了一种利用核函数将线性分类器转换为非线性分类器的方法，详细推导过程见西瓜书p139，这里不赘述