机器学习基础补习08---决策树和随机森林
这篇文章简单写一下两个比较经典的分类算法,决策树和随机森林
决策树
决策树的定义
(1)每个非叶结点表示一种对样本的分割,通常是选用样本的某一个特征,将样本分散到不同子节点中
(2)子节点继续对分散来的样本继续进行分割操作
(3)叶子节点表示输出,每个分散该叶结点中样本都属于同一类(或近似的回归值)
决策树架构
(1)决策树学习:
a.一种根据样本为基础的归纳学习
b.采用的是自顶向下的递归方法:开始数据都在根节点,递归的进行数据分片
c.通过剪枝的方法,防止过拟合
(2)决策树的使用:
a.对未知数据进行分类
b.按照决策树上生成时所采用的分割属性逐层往下,直到一个叶子节点
决策树示意图:
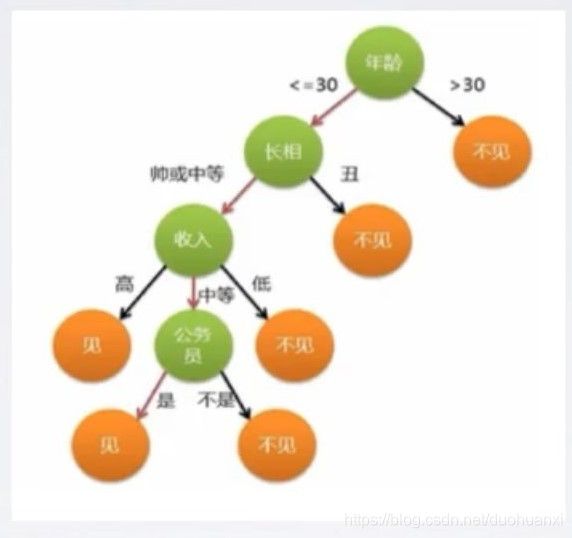
hhh,这个例子有些现实,但是这是一个蛮典型的决策树例子
树的生成方法
(1)如何实现分割?
选择一个特征,设置一个阈值(threshold),Decision Stump
(2)实现什么样的分割?
a.分类效果最好(或分类最纯的、或能使树的路径最短)
b.度量方法
信息增益(ID3)、信息增益率(C4.5)、基尼指数(CART)
信息增益率
(1)某个节点分割前的熵值:经验熵(empirical entropy)
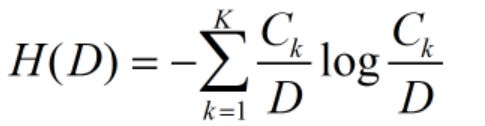
(2)分割后的熵值:经验条件熵
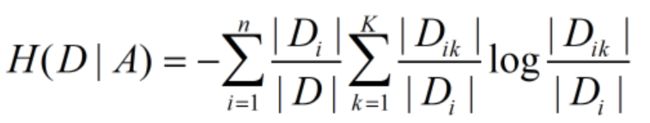
(3)所谓的信息增益率
![]()
我们选择信息增益最大的那个分割
基尼指数
(1)计算方法:

(2)分割后的基尼指数计算,对每个子节点加权求和
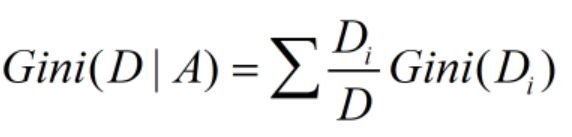
代码如下
#计算某个数据集的Gini指数
var Gini=function(data){
var classNumber={};
for(var i =0;i<data.length;i++){
if(classNumber[data[i].y]==undefined){
classNumber[data[i].y]=1;
}
else{
classNumber[data[i].y]++;
}
}
var sum=0;
var winClass=null;
var winNumber=0;
for(var k in classNumber){
sum=sum+classNumber[k]*classNumber[k]/data.length/data.length;
if(classNumber[k]>winNumber){
winClass=k;
winNumber=classNumber[k];
}
}
return{value:1-sum,'winClass':winClass};
生成方法总结:
执行一个分割的信息增益越大, 表明这个分割对样本的熵减少的能力越强,这个分割所在的特征使得数据由不确定性变成确定性的能力强。
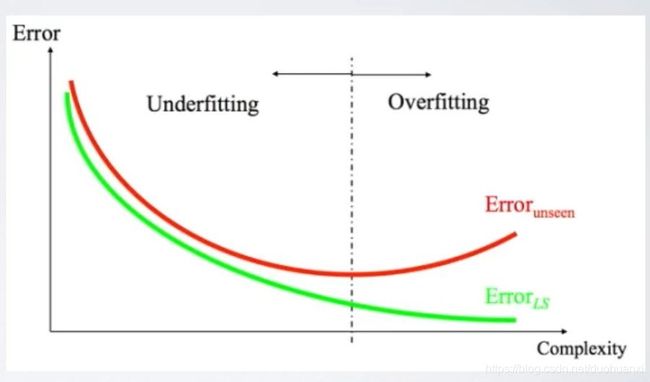
过拟合现象
一个对样本完全分类的树(完整树),容易过拟合,泛化能力较弱
a.样本噪声 b.样本量少
树的剪枝
(1)设计一个树的分类误差评价函数,对所有叶节点的熵加权求和,即:
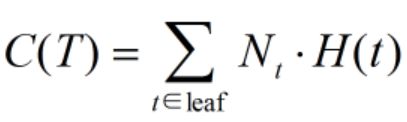
(2)可以使用叶节点数目复杂度评估函数,剪枝的目标就是在这两个函数之间作出平衡,设计出最后的评价函数

(3)因此树的剪枝,就是挑选出完整树的子树,使得评价函数值最小
树的剪枝算法
(1)第一种方法,固定某个经验值α,生成唯一的使得评价函数最小的树
(2)第二种方法,通过迭代操作,构造一些列不同α值,但是评价函数接近的备选树,然后通过交叉验证的方法选择最好的树
如何构造备选树
(1)从完整树开始,当α为0的时候,明显完整树是最优树,即第一个备选树,评价函数值就是 C ( T 0 ) C(T_0) C(T0)
(2)现在裁剪一个r节点,其他部分不动,因此我们可以独立考察r节点构成的单节点树和根节点树的评价函数的变化
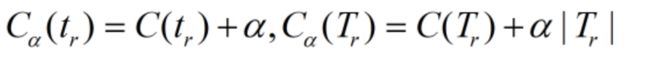
(3)当α比较小的时候, C α ( T r ) < C α ( t r ) C_α(T_r)
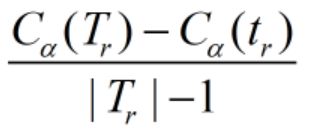
(4)当选择改动最小那个节点之后,我们可以增大α,使得不等式为等式
(5)重复这个迭代过程,直到根节点为止,生成一系列备选树
决策树脑图
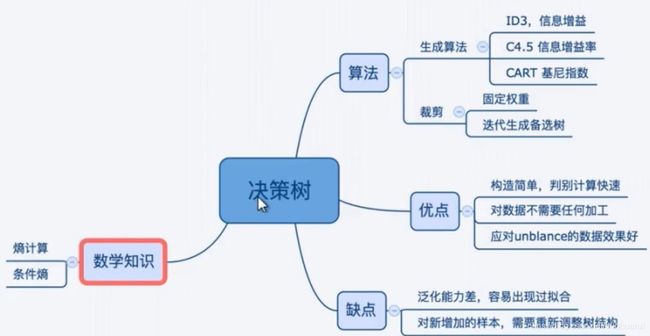
集成学习算法
集成学习算法(ensemble learning)两大利器
a.Bagging
随机森林(Random Forest)是Bagging方法的典型
b.Boosting
后续的AdaBoost,GBDT会详细说明
随机森林算法
(1)通过两个随机性,构造不同的次优树
a.随机选择样本,通过有放回的采样(Boostrap),重复的选择部分样本来构造树
b.构造树的过程中,每次随机考察部分特征,不对树进行裁剪
c.单独采样CART树
(2)在生成一定数目的次优树之后,森林的输出采用简单多数投票法(针对分类)或单颗树输出结果的简单平均(针对回归)得到
随机森林分析
(1)森林中单棵树的分类强度(Strength):每棵树的分类强度越大,则随机森林的分类性能越好
(2)森林中树之间的相关度(Correlation):树之间的相关度越大,则随机森林的分类性能越差
(3)OOB错误率是随机森林的错误率无偏估计
a.对每个样本,在其所有OOB的单树中错误占比,作为OOB错误率
b.因此随机森林不需要进行交叉验证
随机森林脑图
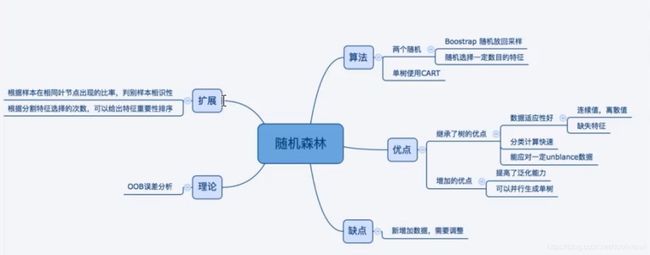
代码实现
var doTest = function() {
logistic.lamb = 0.000;
logistic.alpha = 0.01;
// 对样本作维度扩展
/*
var degree = 3;
for(var i = 0; i < g.samples.length; i++) {
expand( g.samples[i].x, degree);
}
*/
logistic.train(g.samples, 2000);
var result = {};
for(var x = -23; x <= 23; x += 1) {
for(var y = -23; y <= 23; y += 1) {
var sample = [x/10, y/10];
//expand(sample, degree);
var pred = logistic.pred(sample);
result[x/10 + ',' + y/10] = pred;
}
}
// 恢复原始样本
for(var i = 0; i < g.samples.length; i++) {
g.samples[i].x = g.samples[i].x.slice(0, 2);
}
console.log(g.samples);
return result;
}
构造完整的森林
现在可以构造完整的随机森林算法, 包括如何应用随机森林算法
var createForest = function(data, option) {
var treeNumber = option.treeNumber; // 总体树的数目
var bagNumber = option.bagNumber; // Bagging操作的样本数目
var depth = option.depth; // 单棵树的深度
var bestSelect = option.bestSelect; // 选择策略的随机采样次数
var forest = [];
for (var i = 0; i < treeNumber; i++) {
var subData = bagging(data, bagNumber);
forest[i] = createSingleTree(subData, depth, bestSelect);
}
return forest;
};
var bagging = function(data, bagNumber) {
var bag = [];
for( var i = 0; i < bagNumber; i++) {
var n = randi(0, data.length);
bag.push( data[n]);
}
return bag;
};
// 如何利用RF来做分类预测
var predWithTree = function(tree, x) {
for(var i = 0; ; ) {
if (i >= tree.length) {
return null;
}
if ( tree[i].winClass !== undefined ) {
return tree[i].winClass;
}
if ( x[ tree[i].splitFeature] < tree[i].splitValue ) {
i = 2*i + 1;
} else {
i = 2*i + 2;
}
}
};
var predWithForest = function(forest, x) {
var classNumber = {};
for(var i = 0; i < forest.length; i++) {
var pred = predWithTree(forest[i], x);
if ( pred !== null ) {
if ( classNumber[pred] === undefined){
classNumber[pred] = 1;
} else {
classNumber[pred] ++;
}
}
}
var winClass = null;
var winNumber = 0;
for(var k in classNumber ) {
if ( classNumber[k] > winNumber){
winClass = k;
winNumber = classNumber[k];
}
}
return {'winClass': winClass, prob: classNumber[winClass] };
};
RF实现验证
var doTest = function() {
option = {};
option.treeNumber = 32;
option.bagNumber = g.samples.length;
option.depth = 4;
option.bestSelect = 10;
var forest = createForest(g.samples, option);
var result = {};
for(var x = -23; x <= 23; x += 1) {
for(var y = -23; y <= 23; y += 1) {
var sample = [x/10, y/10];
var pred = predWithForest(forest, sample);
result[x/10 + ',' + y/10] = pred;
}
}
return result;
}
感觉今天还是有一些难度,hhh