ML入门2.0 -- 手写决策树(Decision Tree)
ML入门2.0 手写决策树(Decision Tree)
- 决策树简介
- 决策树原理
- 决策树举例
-
-
- 实验截图:
-
- 数据集导入
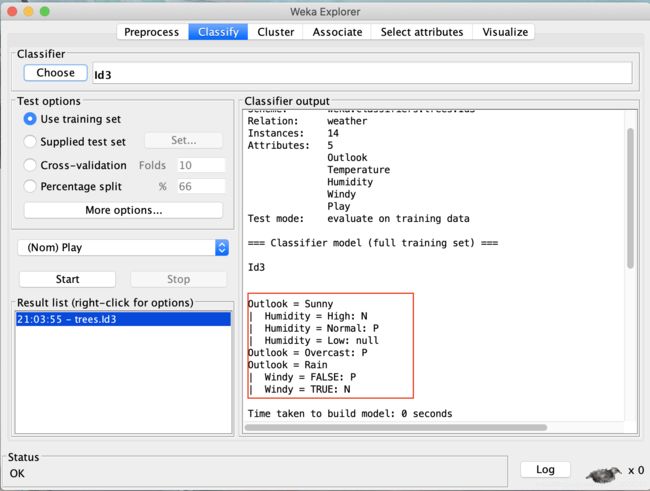
- 使用ID3分类算法
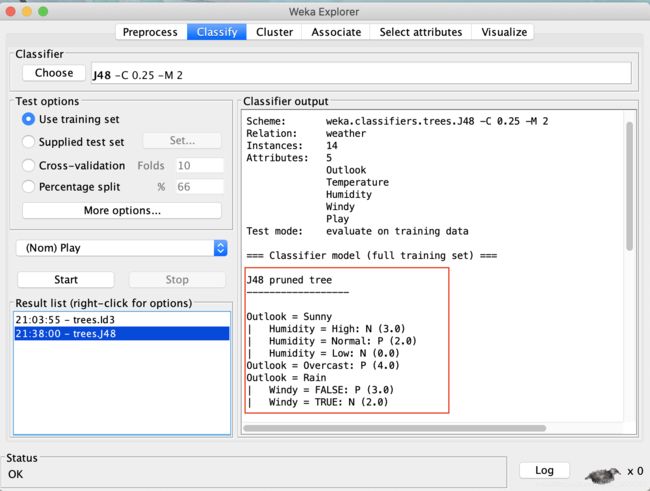
- 使用C4.5(这里是J48)
-
- 手写ID3
-
- 运行结果:
- 完整版程序见githhub
决策树简介
Decision Tree 中文称为决策树,是ML中第二种十分经典的算法,顾名思义其算法结构为树形结构 ,与上一篇博客中介绍的KNN 类似都可以用来解决分类问题的算法。 决策树由下面三种元素构成:
- 根结点 :样本数据的全集
- 内部节点 : 按不同特征属性划分的集合
- 叶节点 : 决策的结果
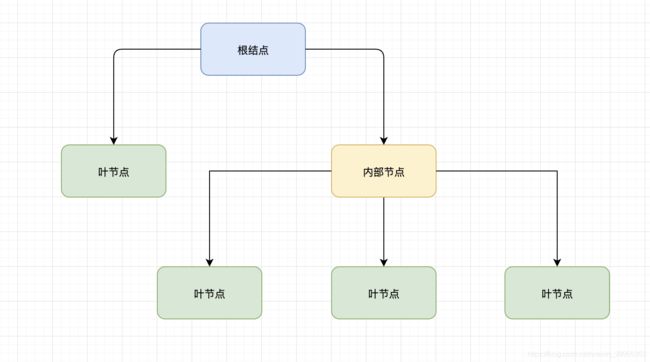
决策树是一种不完全的归纳法,通过层层推理来实现最终的分类,其思想可以类比于程序设计中If-else 分支判断结构,但是if else 是程序员在已知分类结果的基础上设计出的一种固定的判断模式;而决策树则是根据不同的数据集合训练自动给出相应最优的判断模式,实现最终的分类。决策树是最简单的机器学习算法,它易于实现,可解释性强,完全符合人类的直观思维,有着广泛的应用。目前常用的决策树算法有三种:ID3、C4.5、CART。
决策树原理
这里我们主要讲解ID3算法所用的原理,首先需要给出一个定义:信息熵 (entropy),这里表示系统(某个事件)的混乱程度,熵越大混乱程度越大。熵的变化可以看做是信息增益,决策树ID3算法的核心思想是以信息增益度量属性(分类特征)选择,选择分类后信息增益最大的**属性(特征)**进行分类。
首先给出信息熵的计算公式:
随机变量Y的信息熵为(Y为决策变量)1
H ( Y ) = ∑ i = 1 n p ( y i ) log 2 ( 1 / p ( y i ) ) = − ∑ i = 1 n p ( y i ) log 2 p ( y i ) H(Y)=\sum_{i=1}^{n}p(y_i)\log_2(1/p(y_i))=-\sum_{i=1}^{n}p(y_i)\log_2p(y_i) H(Y)=∑i=1np(yi)log2(1/p(yi))=−∑i=1np(yi)log2p(yi)
随机变量Y关于X的条件信息熵为(X为条件变量)
H ( Y ∣ X ) = ∑ i = 1 m p ( x i ) H ( Y ∣ X = x i ) = − ∑ i = 1 m p ( x i ) log 2 p ( y i ∣ x i ) H(Y|X) = \sum_{i=1}^{m}p(x_i)H(Y|X=x_i)=-\sum_{i=1}^{m}p(x_i)\log_2p(y_i|x_i) H(Y∣X)=∑i=1mp(xi)H(Y∣X=xi)=−∑i=1mp(xi)log2p(yi∣xi)
信息增益的公式:
H ( Y ) − H ( Y ∣ X ) H(Y)-H(Y|X) H(Y)−H(Y∣X)
这里给出一点关于信息熵公式的推导:
首先我们需要知道信息得分测量方法,那么我们不妨先考虑测量质量的方法:很久以前一些聪慧的原始人类,选定了一个物体A将其作为参照物,把物体A的质量就称为1千克(KG) ,那么测量其他物体(这里假设测定物体B)的质量时就是观察物体B相当于几个 物体A,这里的几个就是KG前面的系数,那么物体B的质量就等于 几个KG ;那么**几个(n)**的计算公式很简单:n = M(B)/ M(A)
那么现在我们再来思考信息熵的测量:信息的不确定性就是信息熵的量度,先假定一个参照事件A的不确定性,类比质量测定,待测事件B的不确定性的计算就是看待测事件B的不确定性相当于多少个参照事件A的不确定性,这里的多少个就是所谓的信息量。但是不同于质量的是,B的不确定性是又多个A的不确定性相乘得到,举个例子:抛一枚硬币有两种不确定的情况:正面和反面 ,但是抛三枚硬币是的情况是 222 = 2^3 = 8种情况,所以信息的多少个(n)的计算公式就要用指数运算的反函数对数运算来得到,即 n= log2(B);以上阐述是针对待测事件B所有可能情况都是等概率时,那当B的可能情况之间的概率不相等的情况时又该如何测量信息熵? 也不难思考:就是分别测量每种可能情况的信息熵然后乘以该情况的概率 最后再将所有结果相加。所以重点就变成求不同概率情况的信息熵,而概率的倒数恰好就是该概率所对应情况所包含等概率事件的情况个数,例如某事件概率为P=1/10;那么1/P=10就是该事件所含等概率的额情况个数;所以这种情况的信息熵就为n=Plog2(1/P),同理可以求得其他情况的信息熵,最后求和就是上文给出的总信息熵的计算公式 1。
文字解释太枯燥,给出一个解释信息熵的公式的视频:
【学习观11】为什么信息还有单位?如何计算信息量?
最后举个计算信息熵的小例子,假定有四个射击高手:A; B; C; D, 他们获胜的概率分别为P(A)=1/2; P(B)=1/4; P©=P(D)=1/8
设Y为确定哪一位高手获胜
H ( X ) = P ( A ) log 2 ( 1 P ( A ) ) + P ( B ) log 2 ( 1 P ( B ) ) + P ( C ) log 2 ( 1 P ( C ) ) + P ( D ) log 2 ( 1 P ( D ) ) = 1 2 log 2 ( 2 ) + 1 4 log 2 ( 4 ) + 1 8 log 2 ( 8 ) + 1 8 log 2 ( 8 ) = 1 2 + 1 2 + 3 8 + 3 8 = 4 7 b i t s H(X)=P(A)\log_2(\frac{1}{P(A)})+P(B)\log_2(\frac{1}{P(B)})+P(C)\log_2(\frac{1}{P(C)})+P(D)\log_2(\frac{1}{P(D)})=\frac{1}{2}\log_2(2)+\frac{1}{4}\log_2(4)+\frac{1}{8}\log_2(8)+\frac{1}{8}\log_2(8)=\frac{1}{2}+\frac{1}{2}+\frac{3}{8}+\frac{3}{8}=\frac{4}{7}bits H(X)=P(A)log2(P(A)1)+P(B)log2(P(B)1)+P(C)log2(P(C)1)+P(D)log2(P(D)1)=21log2(2)+41log2(4)+81log2(8)+81log2(8)=21+21+83+83=74bits
决策树举例
这里我们给出一个数据集weather与play tennis 以此来构建决策树
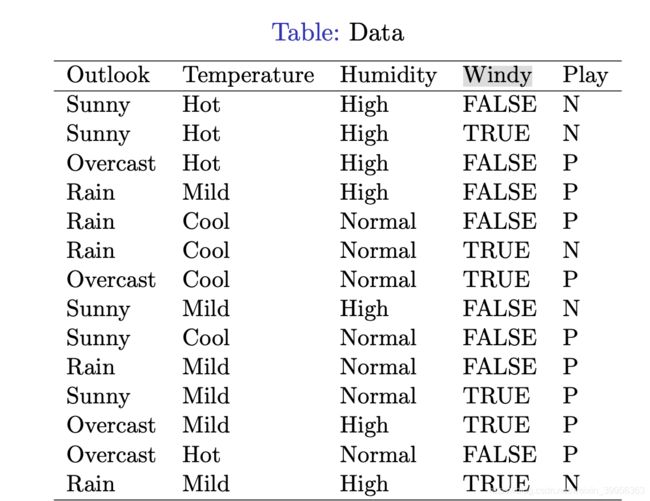
第一种办法采用一个Machine Learning的软件weka来构造
实验截图:
数据集导入
使用ID3分类算法
使用C4.5(这里是J48)
手写ID3
简单的决策树主要分为两个步骤:
训练: 建树 (建立模型)
测试: 用树 (使用模型)
演示使用的数据集依然为上文中的weather数据集
Func1: Loaddata() 制作数据集,加载数据
#Step 1. Load the weather data
def Loaddata():
'''
make the weather dataset
:return: weatherData(原始数据); featureName(天气特征); classValues(分类结果:是否打球)
'''
weatherData = [['Sunny','Hot','High','FALSE','N'],
['Sunny','Hot','High','TRUE','N'],
['Overcast','Hot','High','FALSE','P'],
['Rain','Mild','High','FALSE','P'],
['Rain','Cool','Normal','FALSE','P'],
['Rain','Cool','Normal','TRUE','N'],
['Overcast','Cool','Normal','TRUE','P'],
['Sunny','Mild','High','FALSE','N'],
['Sunny','Cool','Normal','FALSE','P'],
['Rain','Mild','Normal','FALSE','P'],
['Sunny','Mild','Normal','TRUE','P'],
['Overcast','Mild','High','TRUE','P'],
['Overcast','Hot','Normal','FALSE','P'],
['Rain','Mild','High','TRUE','N']]
featureName = ['Outlook', 'Temperature', 'Humidity', 'Windy']
classValues = ['P', 'N']
return weatherData, featureName, classValues
Func2:calcShannonEnt(paraDataSet)计算香农熵
def calcShannonEnt(paraDataSet):
'''
计算给定数据集的香浓熵
:param paraDataSet: 给定数据集
:return: shannonEnt
'''
numInstances = len(paraDataSet) # numInstances:当前给定数据集中数据的个数
labelCounts = {}
for featureVec in paraDataSet: # featureVec:数据集中的单个数据
tempLabel = featureVec[-1]
if tempLabel not in labelCounts.keys():
labelCounts[tempLabel] = 0
labelCounts[tempLabel] += 1
shannonEnt = 0.0
for key in labelCounts.keys():
prob = float(labelCounts[key])/numInstances
shannonEnt -= prob * math.log2(prob)
return shannonEnt
Func3:splitDataSet(dataSet, axis, value) 划分子数据集
def splitDataSet(dataSet, axis, value):
'''
划分该出特征下层的数据集
:param dataSet: 数据集
:param axis: 第几个特征
:param value: 该特征的值
:return: resultDataSet:分类后的数据集
'''
resultDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
# 因为划分当前数据的子集所以去掉当前数据集的分类标准(特征)
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
resultDataSet.append(reducedFeatVec)
return resultDataSet
Func4: chooseBestFeatureToSplit(dataSet) 选出最优的划分特征
def chooseBestFeatureToSplit(dataSet):
'''
选择出最好的特征进行划分子数据集
:param dataSet:数据集
:return: bestFeature:决策出的划分效果最好(信息增益最大的特征)
'''
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
#把第i个属性的所有取值筛选出来组成一个list
featList = [data[i] for data in dataSet]
#去除list中的重复值
uniqueVals = set(featList)
newEntropy = 0.0
#计算条件信息熵
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob*calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if(infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
Func5: majorityCnt(classList) 冲突剪枝
def majorityCnt(classList):
'''
:param classList:
:return:投票决定的类别
'''
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=itemgetter(1), reverse=True)
return sortedClassCount
Func6:creatTree(dataSet, paraFeatureName)建立决策树
def creatTree(dataSet, paraFeatureName):
'''
建树
:param dataSet:数据集
:param paraFeatureName:数据集的属性名称
:return: 递归创建完成的决策树
'''
featureName = paraFeatureName.copy() # 防止后面原本的数据修改导致的分类出错
classList = [example[-1] for example in dataSet]
# 如果当前的label只有一种类别则说明该子集已经完善
if classList.count(classList[0]) == len(classList):
return classList[0]
# 如果遇到属性一致但是结果不同的冲突情形(无分类属性可用),选择占比大的
if len(dataSet) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatureName = featureName[bestFeat]
myTree = {bestFeatureName:{}}
del(featureName[bestFeat])
featvalue = [example[bestFeat] for example in dataSet]
uniqueVals = set(featvalue)
for value in uniqueVals:
subfeatureName = featureName[:]
myTree[bestFeatureName][value] = creatTree(splitDataSet(dataSet, bestFeat, value), subfeatureName)
return myTree
Func7: id3Classify(paraTree, paraTestingSet, featureNames, classValues) ID3分类器
def id3Classify(paraTree, paraTestingSet, featureNames, classValues):
'''
ID3分类器
:param paraTree: 已生成的决策树
:param paraTestingSet: 测试集
:param featureNames: 特征名称
:param classValues: 分类类型值
:return: 正确率
'''
tempCorrect = 0.0
tempTotal = len(paraTestingSet)
tempPrediction = classValues[0]
for featureVector in paraTestingSet:
print("Instance: ", featureVector)
tempTree = paraTree
while True:
for feature in featureNames:
try:
tempTree[feature]
splitFeature = feature
break
except:
i = 1
attributeValue = featureVector[featureNames.index(splitFeature)]
print(splitFeature, " = ", attributeValue)
tempPrediction = tempTree[splitFeature][attributeValue]
if tempPrediction in classValues:
break
else:
tempTree = tempPrediction
print("Prediction = ", tempPrediction)
if featureVector[-1] == tempPrediction:
tempCorrect += 1
return tempCorrect/tempTotal
Func8:STID3Test() 测试程序
def STID3Test():
weatherData, featureName, classValues = Loaddata()
tempTree = creatTree(weatherData, featureName)
print(tempTree)
print("Before classification, feature names = ", featureName)
tempAccuracy = id3Classify(tempTree, weatherData, featureName, classValues)
print("The accuracy of ID3 classifier is {}%".format(tempAccuracy*100))
运行结果:
完整版程序见githhub
github地址