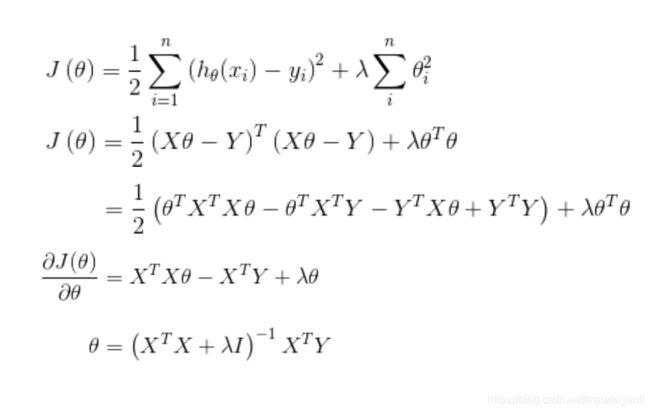机器学习3:岭回归~LASSO回归~弹性网
机器学习3:岭回归 ~LASSO回归 ~弹性网
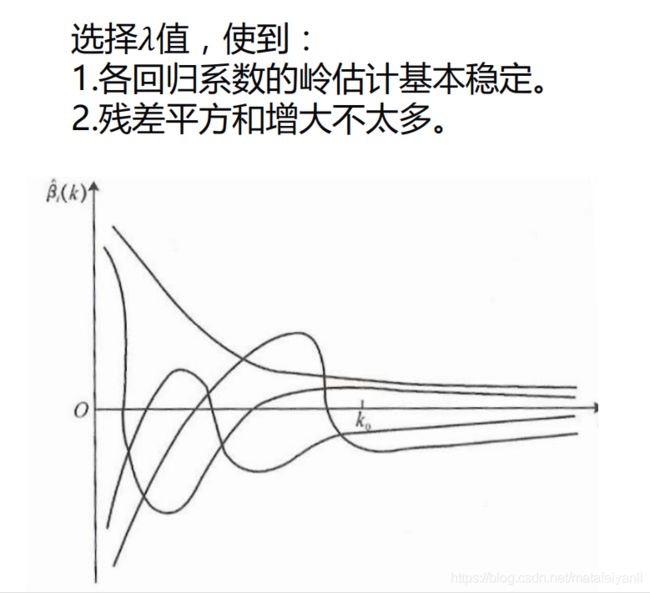
岭回归
算法实现
手工实现
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1,np.newaxis]
print(x_data)
print(y_data)
print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
# 给样本添加偏置项
X_data = np.concatenate((np.ones((16,1)),x_data),axis=1)
print(X_data.shape)
(16, 6)
(16, 1)
(16, 7)
# 岭回归标准方程法求解回归参数
def weights(xArr, yArr,lam=0.2):
xMat = np.mat(xArr)
yMat = np.mat(yArr)
xTx = xMat.T*xMat # 矩阵乘法
rxTx = xTx + np.eye(xMat.shape[1])*lam
# 计算矩阵的值,如果值为0,说明该矩阵没有逆矩阵
if np.linalg.det(rxTx) == 0.0:
print("This matrix cannot do inverse")
return
# xTx.I为xTx的逆矩阵
ws = rxTx.I*xMat.T*yMat
return ws
ws = weights(X_data,y_data)
print(ws)
[[ 7.38107538e-04]
[ 2.07703836e-01]
[ 2.10076376e-02]
[ 5.05385441e-03]
[-1.59173066e+00]
[ 1.10442920e-01]
[-2.42280461e-01]]
# 计算预测值
print(np.mat(X_data)*np.mat(ws))
matrix([[ 83.55075226],
[ 86.92588689],
[ 88.09720228],
[ 90.95677622],
[ 96.06951002],
[ 97.81955375],
[ 98.36444357],
[ 99.99814266],
[103.26832266],
[105.03165135],
[107.45224671],
[109.52190685],
[112.91863666],
[113.98357055],
[115.29845063],
[117.64279933]])
sklearn实现
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)
# 创建模型
# 默认生成50个值,为岭回归系数
alphas_to_test = np.linspace(0.001, 1 ,100)
# 创建模型,保存误差值 Ridge岭回归 CV表示交叉验证
model = linear_model.RidgeCV(alphas=alphas_to_test, store_cv_values=True)
model.fit(x_data, y_data)
# 岭系数,选取50个最佳岭系数
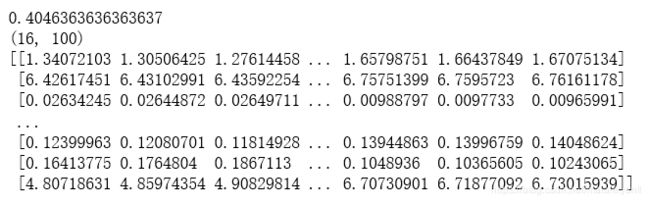
print(model.alpha_)
# loss值 (交叉验证法误差)
print(model.cv_values_.shape)
print(model.cv_values_)
# 画图
# 岭系数跟loss值的关系,对16个样本求平均值
plt.plot(alphas_to_test, model.cv_values_.mean(axis=0))
# 选取的岭系数值的位置
plt.plot(model.alpha_, min(model.cv_values_.mean(axis=0)),'ro')
plt.show()
print(model.predict(x_data[2,np.newaxis]))
[88.11196241]
LASSO回归
原理

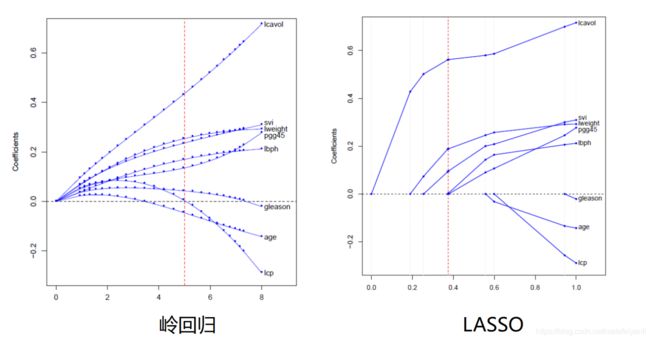
从图中可以看出,LASSO回归可以让有些特征值等于0,而岭回归估计系数等于0的机会微乎其微
蓝色部分是限制正则项<=t,红色部分是代价函数等高线

算法实现
sklearn实现
数据和上述一样
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
#读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)
#创建模型
model=linear_model.LassoCV()
model.fit(x_data,y_data)
#LASSO系数
print(model.alpha_)
#相关系数
print(model.coef_)
20.03464209711722
[0.10206856 0.00409161 0.00354815 0. 0. 0. ]
print(model.predict(x_data[-2,np.newaxis]))
[115.6461414]
弹性网
原理
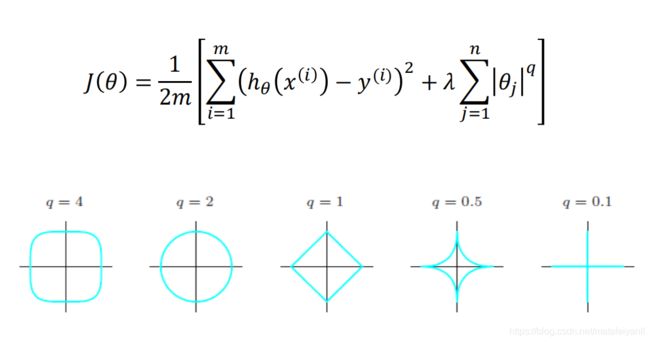

算法实现
sklearn实现
数据和上述相同
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)
# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)
# 创建模型
model = linear_model.ElasticNetCV()
model.fit(x_data, y_data)
# 弹性网系数
print(model.alpha_)
# 相关系数
print(model.coef_)
42.96498005089394
[0.1016487 0.00416716 0.00349843 0. 0. 0. ]
print(model.predict(x_data[-2,np.newaxis]))
[115.6037171]