编译原理——确定有穷自动机的化简-分割法

3.4.4 确定有穷自动机的化简

1.化简的有穷自动机的定义

一个没有多余状态并且没有两个状态是等价的有穷自动机。

多余状态（无用状态）：从该自动机的开始状态出发，任何输入串也不能到达的那个状态

等价状态：

1. 两个状态必须同时为可接受状态（终态）或者不可接受状态（非终态）——一致性条件
2. 对于所有的输入符号，两个状态接受相同的符号必须转换到等价的状态——蔓延性条件

2.分割法

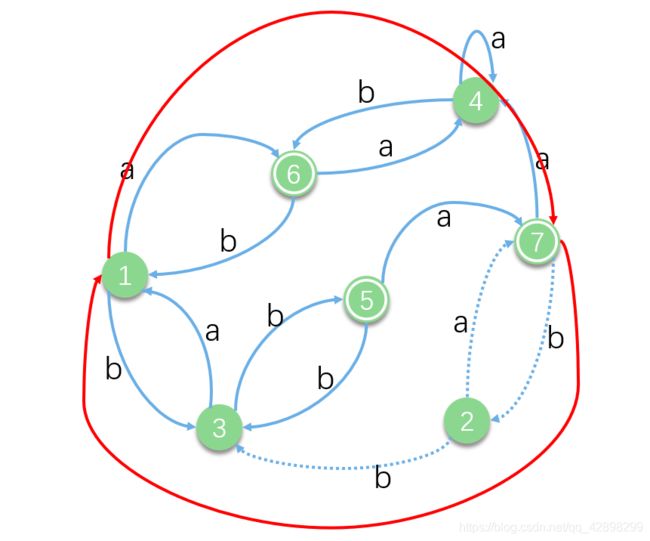
我们首先将其分为终态和非终态

$P_0$ = ({1, 2, 3, 4}, {5, 6, 7})

接下来我们尝试先对{1, 2, 3, 4}这个子集进行划分

$1\stackrel{a}{⟶}6$；$1\stackrel{b}{⟶}3$

$2\stackrel{a}{⟶}7$；$2\stackrel{b}{⟶}3$

$3\stackrel{a}{⟶}1$；$3\stackrel{b}{⟶}5$

$4\stackrel{a}{⟶}4$；$4\stackrel{b}{⟶}6$

首先我们看如果输入a的话，1和2的输出为{5，6，7}这个集合中的元素，而3和4则仍是本集合的元素，所以根据等价状态的第二性质，我们可以将1、2 与3、4分割开。

$P_1$ = ({1, 2}, {3, 4}, {5, 6, 7})

对于目前这个新的集合来说，我们继续划分每个子集。首先从{1,2}开始

$1\stackrel{a}{⟶}6$；$1\stackrel{b}{⟶}3$

$2\stackrel{a}{⟶}7$；$2\stackrel{b}{⟶}3$

我们无论是对1，2输入a还是输入b，它们的输出都属于同一个集合——6、7属于{5,6,7}这个终态集合，3属于{3,4}这个集合，所以{1,2}这个集合很完美，无法划分（即状态无法区分），它俩好得跟一个人似的。

那么我们继续看{3,4}

$3\stackrel{a}{⟶}1$；$3\stackrel{b}{⟶}5$

$4\stackrel{a}{⟶}4$；$4\stackrel{b}{⟶}6$

哦，我们看到，当输入a的时候，3输出的是1，属于{1,2}集合；4则输出的是4，属于{3,4}集合，所以3和4的状态可区分。

那么更新我们的状态图

更新P

$P_2$ = ({1,2}, {3}, {4}, {5, 6, 7})

很明显我们的故事还没结束，还有{5,6,7}这个集合

$5\stackrel{a}{⟶}7$；$5\stackrel{b}{⟶}3$

$6\stackrel{a}{⟶}4$；$6\stackrel{b}{⟶}1$

$7\stackrel{a}{⟶}4$；$7\stackrel{b}{⟶}2$

很明显，在输入a的时候，5的输出为7即{5,6,7} 本集合内的，而6、7则是输出的同一个集合。二话不说，分家！

$P_3$ = ({1,2}, {3}, {4}, {5}, {6, 7})

这时候，还剩{6,7}，如果你上面看明白了，那么到这里你也就懂了，6、7是不可区分的状态。

分割法到此结束……

……不还有最后一步，把所有的不可区分状态统统用其中一个状态来表示就行。

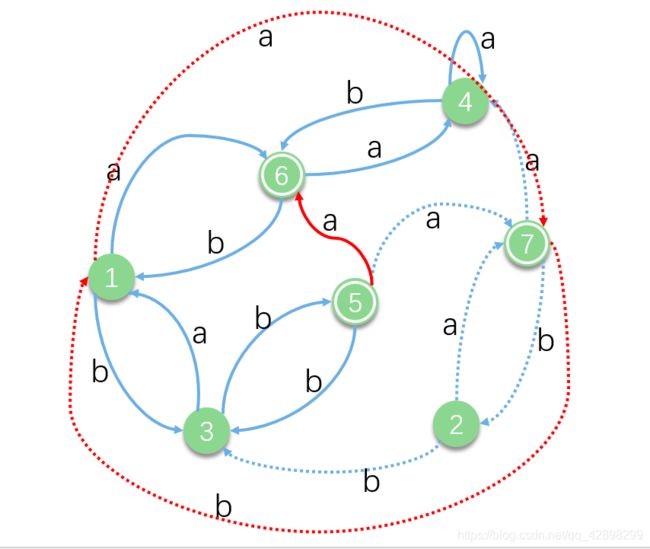
比如1、2，我们直接用1来代替就行，把2所有的输入和输出的压力都放到1身上

（$1\stackrel{b}{⟶}3$，$2\stackrel{b}{⟶}3$ 所以这两个线用一个就行）

然后我们发现6、7可以直接用6代替

把虚线收拾干净再看看

3.The End